216 (number)
| ||||
|---|---|---|---|---|
| Cardinal | two hundred sixteen | |||
| Ordinal | 216th (two hundred sixteenth) | |||
| Factorization | 23 × 33 | |||
| Divisors | 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, 216 | |||
| Greek numeral | ΣΙϚ´ | |||
| Roman numeral | CCXVI | |||
| Binary | 110110002 | |||
| Ternary | 220003 | |||
| Quaternary | 31204 | |||
| Quinary | 13315 | |||
| Senary | 10006 | |||
| Octal | 3308 | |||
| Duodecimal | 16012 | |||
| Hexadecimal | D816 | |||
| Vigesimal | AG20 | |||
| Base 36 | 6036 | |||
216 (two hundred [and] sixteen) is the natural number following 215 and preceding 217. It is a cube, and is often called Plato's number, although it is not certain that this is the number intended by Plato.
In mathematics
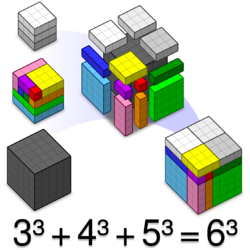
216 is the cube of 6, and the sum of three cubes:[math]\displaystyle{ 216=6^3=3^3+4^3+5^3. }[/math] It is the smallest cube that can be represented as a sum of three positive cubes,[1] making it the first nontrivial example for Euler's sum of powers conjecture. It is, moreover, the smallest number that can be represented as a sum of any number of distinct positive cubes in more than one way.[2] It is a highly powerful number: the product [math]\displaystyle{ 3\times 3 }[/math] of the exponents in its prime factorization [math]\displaystyle{ 216 = 2^3\times 3^3 }[/math] is larger than the product of exponents of any smaller number.[3]
Because there is no way to express it as the sum of the proper divisors of any other integer, it is an untouchable number.[4] Although it is not a semiprime, the three closest numbers on either side of it are, making it the middle number between twin semiprime-triples, the smallest number with this property.[5] Sun Zhiwei has conjectured that each natural number not equal to 216 can be written as either a triangular number or as a triangular number plus a prime number; however, this is not possible for 216. If the conjecture is true, 216 would be the only number for which this is not possible.[6]
There are 216 ordered pairs of four-element permutations whose products generate all the other permutations on four elements.[7] There are also 216 fixed hexominoes, the polyominoes made from 6 squares, joined edge-to-edge. Here "fixed" means that rotations or mirror reflections of hexominoes are considered to be distinct shapes.[8]
In other fields
216 is one common interpretation of Plato's number, a number described in vague terms by Plato in the Republic. Other interpretations include 3600 and 12960000.[9]
There are 216 colors in the web-safe color palette, a [math]\displaystyle{ 6\times 6\times 6 }[/math] color cube.[10]
In the game of checkers, there are 216 different positions that can be reached by the first three moves.[11]
The proto-Kabbalistic work Sefer Yetzirah states that the creation of the world was achieved by the manipulation of 216 sacred letters.[12]
See also
- The year 216
- List of highways numbered 216
- All pages with titles containing 216
References
- ↑ Sloane, N. J. A., ed. "Sequence A066890 (Cubes that are the sum of three distinct positive cubes)". OEIS Foundation. https://oeis.org/A066890.
- ↑ Sloane, N. J. A., ed. "Sequence A003998 (Numbers that are a sum of distinct positive cubes in more than one way)". OEIS Foundation. https://oeis.org/A003998.
- ↑ Sloane, N. J. A., ed. "Sequence A005934 (Highly powerful numbers)". OEIS Foundation. https://oeis.org/A005934.
- ↑ Sloane, N. J. A., ed. "Sequence A005114 (Untouchable numbers, also called nonaliquot numbers: impossible values for the sum of aliquot parts function)". OEIS Foundation. https://oeis.org/A005114.
- ↑ Sloane, N. J. A., ed. "Sequence A202319 (Lesser of two semiprimes sandwiched each between semiprimes thus forming a twin semiprime-triple)". OEIS Foundation. https://oeis.org/A202319.
- ↑ "On sums of primes and triangular numbers". Journal of Combinatorics and Number Theory 1 (1): 65–76. 2009.
- ↑ Sloane, N. J. A., ed. "Sequence A071605 (Number of ordered pairs (a,b) of elements of the symmetric group S_n such that the pair a,b generates S_n)". OEIS Foundation. https://oeis.org/A071605.
- ↑ Sloane, N. J. A., ed. "Sequence A001168 (Number of fixed polyominoes with n cells)". OEIS Foundation. https://oeis.org/A001168.
- ↑ Adam, J. (February 1902). "The arithmetical solution of Plato's number". The Classical Review 16 (1): 17–23. doi:10.1017/S0009840X0020526X. https://zenodo.org/record/1840799.
- ↑ Thomas, B. (1998). "Palette's plunder". IEEE Internet Computing 2 (2): 87–89. doi:10.1109/4236.670691.
- ↑ Sloane, N. J. A., ed. "Sequence A133047 (Starting from the standard 12 against 12 starting position in checkers, the sequence gives the number of distinct positions that can arise after n moves)". OEIS Foundation. https://oeis.org/A133047.
- ↑ Encyclopaedia Judaica, 2nd ed., vol. VI, Keter Publishing House, p. 232
 |