0
| ||||
|---|---|---|---|---|
| Cardinal | 0, zero, "oh" (/oʊ/), nought, naught, nil | |||
| Ordinal | Zeroth, noughth, 0th | |||
| Greek prefix | nulli- | |||
| Binary | 02 | |||
| Ternary | 03 | |||
| Quaternary | 04 | |||
| Quinary | 05 | |||
| Senary | 06 | |||
| Octal | 08 | |||
| Duodecimal | 012 | |||
| Hexadecimal | 016 | |||
| Vigesimal | 020 | |||
| Base 36 | 036 | |||
| Arabic, Kurdish, Persian, Sindhi, Urdu | ٠ | |||
| Hindu numerals | ० | |||
| Chinese | 零, 〇 | |||
| Burmese | ၀ | |||
| Khmer | ០ | |||
| Thai | ๐ | |||
| Assamese, Bengali | ০ | |||
0 (zero) is a number representing an empty quantity. Adding 0 to any number leaves that number unchanged. In mathematical terminology, 0 is the additive identity of the integers, rational numbers, real numbers, and complex numbers, as well as other algebraic structures. Multiplying any number by 0 has the result 0, and consequently, division by zero has no meaning in arithmetic.
As a numerical digit, 0 plays a crucial role in decimal notation: it indicates that the power of ten corresponding to the place containing a 0 does not contribute to the total. For example, "205" in decimal means two hundreds, no tens, and five ones. The same principle applies in place-value notations that uses a base other than ten, such as binary and hexadecimal. The modern use of 0 in this manner derives from Indian mathematics that was transmitted to Europe via medieval Islamic mathematicians and popularized by Fibonacci. It was independently used by the Maya.
Common names for the number 0 in English include zero, nought, naught (/nɔːt/), and nil. In contexts where at least one adjacent digit distinguishes it from the letter O, the number is sometimes pronounced as oh or o (/oʊ/). Informal or slang terms for 0 include zilch and zip. Historically, ought, aught (/ɔːt/), and cipher have also been used.
Etymology
The word zero came into the English language via French zéro from the Italian zero, a contraction of the Venetian zevero form of Italian zefiro via ṣafira or ṣifr.[1] In pre-Islamic time the word Script error: The function "transl" does not exist. (Arabic صفر) had the meaning "empty".[2] Script error: The function "transl" does not exist. evolved to mean zero when it was used to translate Script error: The function "transl" does not exist. (Sanskrit: शून्य) from India.[2] The first known English use of zero was in 1598.[3]
The Italian mathematician Fibonacci (c. 1170 – c. 1250), who grew up in North Africa and is credited with introducing the decimal system to Europe, used the term zephyrum. This became zefiro in Italian, and was then contracted to zero in Venetian. The Italian word zefiro was already in existence (meaning "west wind" from Latin and Greek Zephyrus) and may have influenced the spelling when transcribing Arabic Script error: The function "transl" does not exist..[4]
Modern usage
Depending on the context, there may be different words used for the number zero, or the concept of zero. For the simple notion of lacking, the words "nothing" and "none" are often used. The British English words "nought" or "naught", and "nil" are also synonymous.[5][6]
It is often called "oh" in the context of reading out a string of digits, such as telephone numbers, street addresses, credit card numbers, military time, or years. For example, the area code 201 may be pronounced "two oh one", and the year 1907 is often pronounced "nineteen oh seven". The presence of other digits, indicating that the string contains only numbers, avoids confusion with the letter O. For this reason, systems that include strings with both letters and numbers (such as Canadian postal codes) may exclude the use of the letter O.[citation needed]
Slang words for zero include "zip", "zilch", "nada", and "scratch".[7] In the context of sports, "nil" is sometimes used, especially in British English. Several sports have specific words for a score of zero, such as "love" in tennis – from French l'œuf, "the egg" – and "duck" in cricket, a shortening of "duck's egg". "Goose egg" is another general slang term used for zero.[7]
History
Ancient Near East
| nfr |
heart with trachea beautiful, pleasant, good |
<hiero>F35</hiero> |
|---|
Ancient Egyptian numerals were of base 10.[8] They used hieroglyphs for the digits and were not positional. In one papyrus written around 1770 BC, a scribe recorded daily incomes and expenditures for the pharaoh's court, using the nfr hieroglyph to indicate cases where the amount of a foodstuff received was exactly equal to the amount disbursed. Egyptologist Alan Gardiner suggested that the nfr hieroglyph was being used as a symbol for zero. The same symbol was also used to indicate the base level in drawings of tombs and pyramids, and distances were measured relative to the base line as being above or below this line.[9]
By the middle of the 2nd millennium BC, Babylonian mathematics had a sophisticated base 60 positional numeral system. The lack of a positional value (or zero) was indicated by a space between sexagesimal numerals. In a tablet unearthed at Kish (dating to as early as 700 BC), the scribe Bêl-bân-aplu used three hooks as a placeholder in the same Babylonian system.[10] By 300 BC, a punctuation symbol (two slanted wedges) was repurposed as a placeholder.[11][12]
The Babylonian positional numeral system differed from the later Hindu–Arabic system in that it did not explicitly specify the magnitude of the leading sexagesimal digit, so that for example the lone digit 1 (![]() ) might represent any of 1, 60, 3600 = 602, etc., similar to the significand of a floating-point number but without an explicit exponent, and so only distinguished implicitly from context. The zero-like placeholder mark was only ever used in between digits, but never alone or at the end of a number.[13]
) might represent any of 1, 60, 3600 = 602, etc., similar to the significand of a floating-point number but without an explicit exponent, and so only distinguished implicitly from context. The zero-like placeholder mark was only ever used in between digits, but never alone or at the end of a number.[13]
Pre-Columbian Americas

The Mesoamerican Long Count calendar developed in south-central Mexico and Central America required the use of zero as a placeholder within its vigesimal (base-20) positional numeral system. Many different glyphs, including the partial quatrefoil were used as a zero symbol for these Long Count dates, the earliest of which (on Stela 2 at Chiapa de Corzo, Chiapas) has a date of 36 BC.[lower-alpha 1][14]
Since the eight earliest Long Count dates appear outside the Maya homeland,[15] it is generally believed that the use of zero in the Americas predated the Maya and was possibly the invention of the Olmecs.[16] Many of the earliest Long Count dates were found within the Olmec heartland, although the Olmec civilization ended by the 4th century BC, several centuries before the earliest known Long Count dates.[citation needed]
Although zero became an integral part of Maya numerals, with a different, empty tortoise-like "shell shape" used for many depictions of the "zero" numeral, it is assumed not to have influenced Old World numeral systems.[citation needed]
Quipu, a knotted cord device, used in the Inca Empire and its predecessor societies in the Andean region to record accounting and other digital data, is encoded in a base ten positional system. Zero is represented by the absence of a knot in the appropriate position.[citation needed]
Classical antiquity
The Ancient Greece had no symbol for zero (μηδέν, pronounced 'midén'), and did not use a digit placeholder for it.[17] According to mathematician Charles Seife, the ancient Greeks did begin to adopt the Babylonian placeholder zero for their work in astronomy after 500 BC, representing it with the lowercase Greek letter ό (όμικρον: omicron). However, after using the Babylonian placeholder zero for astronomical calculations they would typically convert the numbers back into Greek numerals. Greeks seemed to have a philosophical opposition to using zero as a number.[18] Other scholars give the Greek partial adoption of the Babylonian zero a later date, with neuroscientist Andreas Nieder giving a date of after 400 BC and mathematician Robert Kaplan dating it after the conquests of Alexander.[19][20]
Greeks seemed unsure about the status of zero as a number. Some of them asked themselves, "How can not being be?", leading to philosophical and, by the medieval period, religious arguments about the nature and existence of zero and the vacuum. The paradoxes of Zeno of Elea depend in large part on the uncertain interpretation of zero.[21]

By AD 150, Ptolemy, influenced by Hipparchus and the Babylonians, was using a symbol for zero ()[22][23] in his work on mathematical astronomy called the Syntaxis Mathematica, also known as the Almagest.[24] This Hellenistic zero was perhaps the earliest documented use of a numeral representing zero in the Old World.[25] Ptolemy used it many times in his Almagest (VI.8) for the magnitude of solar and lunar eclipses. It represented the value of both digits and minutes of immersion at first and last contact. Digits varied continuously from 0 to 12 to 0 as the Moon passed over the Sun (a triangular pulse), where twelve digits was the angular diameter of the Sun. Minutes of immersion was tabulated from 0′0″ to 31′20″ to 0′0″, where 0′0″ used the symbol as a placeholder in two positions of his sexagesimal positional numeral system,[lower-alpha 2] while the combination meant a zero angle. Minutes of immersion was also a continuous function 1/12 31′20″ √d(24−d) (a triangular pulse with convex sides), where d was the digit function and 31′20″ was the sum of the radii of the Sun's and Moon's discs.[26] Ptolemy's symbol was a placeholder as well as a number used by two continuous mathematical functions, one within another, so it meant zero, not none.
The earliest use of zero in the calculation of the Julian Easter occurred before AD 311, at the first entry in a table of epacts as preserved in an Ethiopic document for the years 311 to 369, using a Ge'ez word for "none" (English translation is "0" elsewhere) alongside Ge'ez numerals (based on Greek numerals), which was translated from an equivalent table published by the Church of Alexandria in Medieval Greek.[27] This use was repeated in 525 in an equivalent table, that was translated via the Latin nulla ("none") by Dionysius Exiguus, alongside Roman numerals.[28] When division produced zero as a remainder, nihil, meaning "nothing", was used. These medieval zeros were used by all future medieval calculators of Easter. The initial "N" was used as a zero symbol in a table of Roman numerals by Bede—or his colleagues—around AD 725.[29]
In most cultures, 0 was identified before the idea of negative things (i.e., quantities less than zero) was accepted.
China
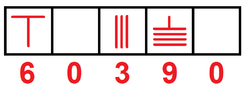
The Sūnzĭ Suànjīng, of unknown date but estimated to be dated from the 1st to 5th centuries AD, and Japanese records dated from the 18th century, describe how the 4th century BC Chinese counting rods system enabled one to perform decimal calculations. As noted in the Xiahou Yang Suanjing (425–468 AD), to multiply or divide a number by 10, 100, 1000, or 10000, all one needs to do, with rods on the counting board, is to move them forwards, or back, by 1, 2, 3, or 4 places.[31] According to A History of Mathematics, the rods "gave the decimal representation of a number, with an empty space denoting zero".[30] The counting rod system is considered a positional notation system.[32]
Zero was not treated as a number at that time, but as a "vacant position".[33] Qín Jiǔsháo's 1247 Mathematical Treatise in Nine Sections is the oldest surviving Chinese mathematical text using a round symbol 〇 for zero.[34] The origin of this symbol is unknown; it may have been borrowed from Indian sources or produced by modifying a square symbol.[35] Chinese authors had been familiar with the idea of negative numbers by the Han dynasty (2nd century AD), as seen in The Nine Chapters on the Mathematical Art.[36]
India
Pingala (c. 3rd or 2nd century BC),[37] a Sanskrit prosody scholar,[38] used binary numbers in the form of short and long syllables (the latter equal in length to two short syllables), a notation similar to Morse code.[39] Pingala used the Sanskrit word śūnya explicitly to refer to zero.[37]
The concept of zero as a written digit in the decimal place value notation was developed in India.[40] A symbol for zero, a large dot likely to be the precursor of the still-current hollow symbol, is used throughout the Bakhshali manuscript, a practical manual on arithmetic for merchants.[41] In 2017, three samples from the manuscript were shown by radiocarbon dating to come from three different centuries: from AD 224–383, AD 680–779, and AD 885–993, making it South Asia's oldest recorded use of the zero symbol. It is not known how the birch bark fragments from different centuries forming the manuscript came to be packaged together.[42][43][44]
The Lokavibhāga, a Jain text on cosmology surviving in a medieval Sanskrit translation of the Prakrit original, which is internally dated to AD 458 (Saka era 380), uses a decimal place-value system, including a zero. In this text, śūnya ("void, empty") is also used to refer to zero.[45]
The Aryabhatiya (c. 500), states sthānāt sthānaṁ daśaguṇaṁ syāt "from place to place each is ten times the preceding".[46][47][48]
Rules governing the use of zero appeared in Brahmagupta's Brahmasputha Siddhanta (7th century), which states the sum of zero with itself as zero, and incorrectly describes division by zero in the following way:[49][50]
A positive or negative number when divided by zero is a fraction with the zero as denominator. Zero divided by a negative or positive number is either zero or is expressed as a fraction with zero as numerator and the finite quantity as denominator. Zero divided by zero is zero.
Epigraphy
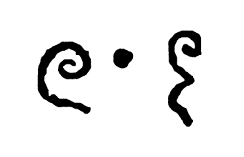
A black dot is used as a decimal placeholder in the Bakhshali manuscript, portions of which date from AD 224–993.[42]
There are numerous copper plate inscriptions, with the same small O in them, some of them possibly dated to the 6th century, but their date or authenticity may be open to doubt.[10]
A stone tablet found in the ruins of a temple near Sambor on the Mekong, Kratié Province, Cambodia, includes the inscription of "605" in Khmer numerals (a set of numeral glyphs for the Hindu–Arabic numeral system). The number is the year of the inscription in the Saka era, corresponding to a date of AD 683.[51]
The first known use of special glyphs for the decimal digits that includes the indubitable appearance of a symbol for the digit zero, a small circle, appears on a stone inscription found at the Chaturbhuj Temple, Gwalior, in India, dated 876.[52][53]
Middle Ages
Transmission to Islamic culture
The Arabic-language inheritance of science was largely Greek,[54] followed by Hindu influences.[55] In 773, at Al-Mansur's behest, translations were made of many ancient treatises including Greek, Roman, Indian, and others.
In AD 813, astronomical tables were prepared by a Persian mathematician, Muḥammad ibn Mūsā al-Khwārizmī, using Hindu numerals;[55] and about 825, he published a book synthesizing Greek and Hindu knowledge and also contained his own contribution to mathematics including an explanation of the use of zero.[56] This book was later translated into Latin in the 12th century under the title Algoritmi de numero Indorum. This title means "al-Khwarizmi on the Numerals of the Indians". The word "Algoritmi" was the translator's Latinization of Al-Khwarizmi's name, and the word "Algorithm" or "Algorism" started to acquire a meaning of any arithmetic based on decimals.[55]
Muhammad ibn Ahmad al-Khwarizmi, in 976, stated that if no number appears in the place of tens in a calculation, a little circle should be used "to keep the rows". This circle was called ṣifr.[57]
Transmission to Europe
The Hindu–Arabic numeral system (base 10) reached Western Europe in the 11th century, via Al-Andalus, through Spanish Muslims, the Moors, together with knowledge of classical astronomy and instruments like the astrolabe. Gerbert of Aurillac is credited with reintroducing the lost teachings into Catholic Europe. For this reason, the numerals came to be known in Europe as "Arabic numerals". The Italian mathematician Fibonacci or Leonardo of Pisa was instrumental in bringing the system into European mathematics in 1202, stating:
After my father's appointment by his homeland as state official in the customs house of Bugia for the Pisan merchants who thronged to it, he took charge; and in view of its future usefulness and convenience, had me in my boyhood come to him and there wanted me to devote myself to and be instructed in the study of calculation for some days. There, following my introduction, as a consequence of marvelous instruction in the art, to the nine digits of the Hindus, the knowledge of the art very much appealed to me before all others, and for it I realized that all its aspects were studied in Egypt, Syria, Greece, Sicily, and Provence, with their varying methods; and at these places thereafter, while on business. I pursued my study in depth and learned the give-and-take of disputation. But all this even, and the algorism, as well as the art of Pythagoras, I considered as almost a mistake in respect to the method of the Hindus [Modus Indorum]. Therefore, embracing more stringently that method of the Hindus, and taking stricter pains in its study, while adding certain things from my own understanding and inserting also certain things from the niceties of Euclid's geometric art. I have striven to compose this book in its entirety as understandably as I could, dividing it into fifteen chapters. Almost everything which I have introduced I have displayed with exact proof, in order that those further seeking this knowledge, with its pre-eminent method, might be instructed, and further, in order that the Latin people might not be discovered to be without it, as they have been up to now. If I have perchance omitted anything more or less proper or necessary, I beg indulgence, since there is no one who is blameless and utterly provident in all things. The nine Indian figures are: 9 8 7 6 5 4 3 2 1. With these nine figures, and with the sign 0 ... any number may be written.[58]
From the 13th century, manuals on calculation (adding, multiplying, extracting roots, etc.) became common in Europe where they were called algorismus after the Persian mathematician al-Khwārizmī. One popular manual was written by Johannes de Sacrobosco in the early 1200s and was one of the earliest scientific books to be printed, in 1488.[59][60] The practice of calculating on paper using Hindu–Arabic numerals only gradually displaced calculation by abacus and recording with Roman numerals.[61] In the 16th century, Hindu–Arabic numerals became the predominant numerals used in Europe.[59]
Symbols and representations


Today, the numerical digit 0 is usually written as a circle or ellipse. Traditionally, many print typefaces made the capital letter O more rounded than the narrower, elliptical digit 0.[62] Typewriters originally made no distinction in shape between O and 0; some models did not even have a separate key for the digit 0. The distinction came into prominence on modern character displays.[62]
A slashed zero () is often used to distinguish the number from the letter (mostly in computing, navigation and in the military, for example). The digit 0 with a dot in the center seems to have originated as an option on IBM 3270 displays and has continued with some modern computer typefaces such as Andalé Mono, and in some airline reservation systems. One variation uses a short vertical bar instead of the dot. Some fonts designed for use with computers made one of the capital-O–digit-0 pair more rounded and the other more angular (closer to a rectangle). A further distinction is made in falsification-hindering typeface as used on German car number plates by slitting open the digit 0 on the upper right side. In some systems either the letter O or the numeral 0, or both, are excluded from use, to avoid confusion.
Mathematics
The concept of zero plays multiple roles in mathematics: as a digit, it is an important part of positional notation for representing numbers, while it also plays an important role as a number in its own right in many algebraic settings.
As a digit
In positional number systems (such as the usual decimal notation for representing numbers), the digit 0 plays the role of a placeholder, indicating that certain powers of the base do not contribute. For example, the decimal number 205 is the sum of two hundreds and five ones, with the 0 digit indicating that no tens are added. The digit plays the same role in decimal fractions and in the decimal representation of other real numbers (indicating whether any tenths, hundredths, thousandths, etc., are present) and in bases other than 10 (for example, in binary, where it indicates which powers of 2 are omitted).[63]
Elementary algebra

The number 0 is the smallest nonnegative integer. The natural number following 0 is 1 and no natural number precedes 0. The number 0 may or may not be considered a natural number,[64][65] but it is an integer, and hence a rational number and a real number.[66] All rational numbers are algebraic numbers, including 0. When the real numbers are extended to form the complex numbers, 0 becomes the origin of the complex plane.
The number 0 can be regarded as neither positive nor negative[67] or, alternatively, both positive and negative[68] and is usually displayed as the central number in a number line. Zero is even[69] (that is, a multiple of 2), and is also an integer multiple of any other integer, rational, or real number. It is neither a prime number nor a composite number: it is not prime because prime numbers are greater than 1 by definition, and it is not composite because it cannot be expressed as the product of two smaller natural numbers.[70] (However, the singleton set {0} is a prime ideal in the ring of the integers.)
The following are some basic rules for dealing with the number 0. These rules apply for any real or complex number x, unless otherwise stated.
- Addition: x + 0 = 0 + x = x. That is, 0 is an identity element (or neutral element) with respect to addition.
- Subtraction: x − 0 = x and 0 − x = −x.
- Multiplication: x · 0 = 0 · x = 0.
- Division: 0/x = 0, for nonzero x. But x/0 is undefined, because 0 has no multiplicative inverse (no real number multiplied by 0 produces 1), a consequence of the previous rule.[71]
- Exponentiation: x0 = x/x = 1, except that the case x = 0 is considered undefined in some contexts. For all positive real x, 0x = 0.
The expression 0/0, which may be obtained in an attempt to determine the limit of an expression of the form f(x)/g(x) as a result of applying the lim operator independently to both operands of the fraction, is a so-called "indeterminate form". That does not mean that the limit sought is necessarily undefined; rather, it means that the limit of f(x)/g(x), if it exists, must be found by another method, such as l'Hôpital's rule.[72]
The sum of 0 numbers (the empty sum) is 0, and the product of 0 numbers (the empty product) is 1. The factorial 0! evaluates to 1, as a special case of the empty product.[73]
Other uses in mathematics

The role of 0 as the smallest counting number can be generalized or extended in various ways. In set theory, 0 is the cardinality of the empty set: if one does not have any apples, then one has 0 apples. In fact, in certain axiomatic developments of mathematics from set theory, 0 is defined to be the empty set.[74] When this is done, the empty set is the von Neumann cardinal assignment for a set with no elements, which is the empty set. The cardinality function, applied to the empty set, returns the empty set as a value, thereby assigning it 0 elements.
Also in set theory, 0 is the lowest ordinal number, corresponding to the empty set viewed as a well-ordered set. In order theory (and especially its subfield lattice theory), 0 may denote the least element of a lattice or other partially ordered set.
The role of 0 as additive identity generalizes beyond elementary algebra. In abstract algebra, 0 is commonly used to denote a zero element, which is the identity element for addition (if defined on the structure under consideration) and an absorbing element for multiplication (if defined). (Such elements may also be called zero elements.) Examples include identity elements of additive groups and vector spaces. Another example is the zero function (or zero map) on a domain D. This is the constant function with 0 as its only possible output value, that is, it is the function f defined by f(x) = 0 for all x in D. As a function from the real numbers to the real numbers, the zero function is the only function that is both even and odd.
The number 0 is also used in several other ways within various branches of mathematics:
- A zero of a function f is a point x in the domain of the function such that f(x) = 0.
- In propositional logic, 0 may be used to denote the truth value false.
- In probability theory, 0 is the smallest allowed value for the probability of any event.[75]
- Category theory introduces the idea of a zero object, often denoted 0, and the related concept of zero morphisms, which generalize the zero function.[76]
Physics
The value zero plays a special role for many physical quantities. For some quantities, the zero level is naturally distinguished from all other levels, whereas for others it is more or less arbitrarily chosen. For example, for an absolute temperature (typically measured in kelvins), zero is the lowest possible value. (Negative temperatures can be defined for some physical systems, but negative-temperature systems are not actually colder.) This is in contrast to temperatures on the Celsius scale, for example, where zero is arbitrarily defined to be at the freezing point of water.[77][78] Measuring sound intensity in decibels or phons, the zero level is arbitrarily set at a reference value—for example, at a value for the threshold of hearing. In physics, the zero-point energy is the lowest possible energy that a quantum mechanical physical system may possess and is the energy of the ground state of the system.
Computer science
Modern computers store information in binary, that is, using an "alphabet" that contains only two symbols, usually chosen to be "0" and "1". Binary coding is convenient for digital electronics, where "0" and "1" can stand for the absence or presence of electrical current in a wire.[79] Computer programmers typically use high-level programming languages that are more easily intelligible to humans than the binary instructions that are directly executed by the central processing unit. 0 plays various important roles in high-level languages. For example, a Boolean variable stores a value that is either true or false, and 0 is often the numerical representation of false.[80]
0 also plays a role in array indexing. The most common practice throughout human history has been to start counting at one, and this is the practice in early classic programming languages such as Fortran and COBOL. However, in the late 1950s LISP introduced zero-based numbering for arrays while Algol 58 introduced completely flexible basing for array subscripts (allowing any positive, negative, or zero integer as base for array subscripts), and most subsequent programming languages adopted one or other of these positions. For example, the elements of an array are numbered starting from 0 in C, so that for an array of n items the sequence of array indices runs from 0 to n−1.[citation needed]
There can be confusion between 0- and 1-based indexing; for example, Java's JDBC indexes parameters from 1 although Java itself uses 0-based indexing.[81]
In C, a byte containing the value 0 serves to indicate where a string of characters ends. Also, 0 is a standard way to refer to a null pointer in code.[82]
In databases, it is possible for a field not to have a value. It is then said to have a null value.[83] For numeric fields it is not the value zero. For text fields this is not blank nor the empty string. The presence of null values leads to three-valued logic. No longer is a condition either true or false, but it can be undetermined. Any computation including a null value delivers a null result.[84]
In mathematics, there is no "positive zero" or "negative zero" distinct from zero; both −0 and +0 represent exactly the same number. However, in some computer hardware signed number representations, zero has two distinct representations, a positive one grouped with the positive numbers and a negative one grouped with the negatives. This kind of dual representation is known as signed zero, with the latter form sometimes called negative zero. These representations include the signed magnitude and ones' complement binary integer representations (but not the two's complement binary form used in most modern computers), and most floating-point number representations (such as IEEE 754 and IBM S/390 floating-point formats).[citation needed]
An epoch, in computing terminology, is the date and time associated with a zero timestamp. The Unix epoch begins the midnight before the first of January 1970.[85][86][87] The Classic Mac OS epoch and Palm OS epoch begin the midnight before the first of January 1904.[88]
Many APIs and operating systems that require applications to return an integer value as an exit status typically use zero to indicate success and non-zero values to indicate specific error or warning conditions.[citation needed]
Programmers often use a slashed zero to avoid confusion with the letter "O".[89]
Other fields
Biology
In comparative zoology and cognitive science, recognition that some animals display awareness of the concept of zero leads to the conclusion that the capability for numerical abstraction arose early in the evolution of species.[90]
Dating systems
In the BC calendar era, the year 1 BC is the first year before AD 1; there is not a year zero. By contrast, in astronomical year numbering, the year 1 BC is numbered 0, the year 2 BC is numbered −1, and so forth.[91]
See also
- Grammatical number
- Mathematical constant
- Number theory
- Peano axioms
Notes
- ↑ No long count date actually using the number 0 has been found before the 3rd century AD, but since the long count system would make no sense without some placeholder, and since Mesoamerican glyphs do not typically leave empty spaces, these earlier dates are taken as indirect evidence that the concept of 0 already existed at the time.
- ↑ Each place in Ptolemy's sexagesimal system was written in Greek numerals from 0 to 59, where 31 was written λα meaning 30+1, and 20 was written κ meaning 20.
References
- ↑
- Harper, Douglas (2011). "Etymonline Etymology Dictionary". Etymonline Etymology Dictionary. ""figure which stands for naught in the Arabic notation," also "the absence of all quantity considered as quantity", c. 1600, from French zéro or directly from Italian zero, from Medieval Latin zephirum, from Arabic sifr "cipher", translation of Sanskrit sunya-m "empty place, desert, naught"".
- Menninger, Karl (1992). Number Words and Number Symbols: A cultural history of numbers. Courier Dover Publications. pp. 399–404. ISBN 978-0-486-27096-8. https://books.google.com/books?id=BFJHzSIj2u0C. Retrieved 5 January 2016.
- "zero, n.". Oxford University Press. December 2011. http://www.oed.com/view/Entry/232803?rskey=zGcSoq&result=1&isAdvanced=false. ""French zéro (1515 in Hatzfeld & Darmesteter) or its source Italian zero, for *zefiro, < Arabic çifr""
- ↑ 2.0 2.1
- Smithsonian Institution. Oriental Elements of Culture in the Occident, p. 518, at Google Books. Annual Report of the Board of Regents of the Smithsonian Institution; Harvard University Archives. "Sifr occurs in the meaning of "empty" even in the pre-Islamic time. ... Arabic sifr in the meaning of zero is a translation of the corresponding India sunya."
- Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W.W. Norton & Co.. ISBN 978-0-393-04002-9. "Zero derives from Hindu sunya – meaning void, emptiness – via Arabic sifr, Latin cephirum, Italian zevero."
- Logan, Robert (2010). The Poetry of Physics and the Physics of Poetry. World Scientific. ISBN 978-981-4295-92-5. "The idea of sunya and place numbers was transmitted to the Arabs who translated sunya or "leave a space" into their language as sifr."
- ↑ "Merriam Webster online Dictionary". Merriam Webster online Dictionary. }}
- ↑ Ifrah 2000, p. 589
- ↑ "Collins - Free online dictionary". https://www.collinsdictionary.com/dictionary/english/nought.
- ↑ "Collins - Free online dictionary, thesaurus and reference materials - nill". https://www.collinsdictionary.com/dictionary/english/nil.
- ↑ 7.0 7.1 "'Aught' synonyms". Thesaurus.com. http://thesaurus.com/browse/aught#visualthesaurus.
- ↑ "Egyptian numerals". University of St Andrews. 2000. http://mathshistory.st-andrews.ac.uk/HistTopics/Egyptian_numerals.html.
- ↑ Lumpkin, Beatrice (2002). "Mathematics Used in Egyptian Construction and Bookkeeping". The Mathematical Intelligencer 24 (2): 20–25. doi:10.1007/BF03024613.
- ↑ 10.0 10.1 Kaplan 2000.
- ↑ "Zero" (in en). University of St Andrews. 2000. https://mathshistory.st-andrews.ac.uk/HistTopics/Zero/.
- ↑ "Babylonian mathematics". 2016. https://www.open.edu/openlearn/ocw/mod/oucontent/view.php?printable=1&id=1976.
- ↑ Reimer 2014, p. 172.
- ↑ "Cyclical views of time". https://www.mexicolore.co.uk/aztecs/calendar/cyclical-views-of-time.
- ↑ Diehl (2004), p. 186.
- ↑ Mortaigne, Véronique (28 November 2014). "The golden age of Mayan civilisation – exhibition review". The Guardian. https://www.theguardian.com/culture/2014/nov/28/mayan-civilisation-paris-exhibition.
- ↑ Wallin, Nils-Bertil (19 November 2002). "The History of Zero". The Whitney and Betty Macmillan Center for International and Area Studies at Yale.. http://yaleglobal.yale.edu/about/zero.jsp.
- ↑ Seife, Charles (1 September 2000). Zero: The Biography of a Dangerous Idea. Penguin. p. 39. ISBN 978-0-14-029647-1. OCLC 1005913932. https://books.google.com/books?id=obJ70nxVYFUC. Retrieved 30 April 2022.
- ↑ Nieder, Andreas (19 November 2019). A Brain for Numbers: The Biology of the Number Instinct. MIT Press. p. 286. ISBN 978-0-262-35432-5. https://books.google.com/books?id=x4y5DwAAQBAJ&pg=PA286. Retrieved 30 April 2022.
- ↑ Kaplan 2000, p. 17.
- ↑ Huggett, Nick (2019). "Zeno's Paradoxes". in Zalta, Edward N.. The Stanford Encyclopedia of Philosophy (Winter 2019 ed.). Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/archives/win2019/entries/paradox-zeno/. Retrieved 2020-08-09.
- ↑ Neugebauer, Otto (1969). The Exact Sciences in Antiquity (2 ed.). Dover Publications. pp. 13–14, plate 2. ISBN 978-0-486-22332-2. https://archive.org/details/exactsciencesant00neug.
- ↑ Mercier, Raymond. "Consideration of the Greek symbol 'zero'". Home of Kairos. http://www.raymondm.co.uk/prog/GreekZeroSign.pdf.[self-published source?]
- ↑ Ptolemy (1998). Ptolemy's Almagest. Princeton University Press. pp. 306–307. ISBN 0-691-00260-6.
- ↑ O'Connor, J J; Robertson, E F. "A history of Zero". MacTutor History of Mathematics. http://mathshistory.st-andrews.ac.uk/HistTopics/Zero.html.
- ↑ Pedersen, Olaf (2010). Alexander Jones. ed. A Survey of the Almagest. Sources and Studies in the History of Mathematics and Physical Sciences. Springer. pp. 232–235. doi:10.1007/978-0-387-84826-6_7. ISBN 978-0-387-84825-9.
- ↑ Neugebauer, Otto (2016). Ethiopic Astronomy and Computus (Red Sea Press ed.). Red Sea Press. pp. 25, 53, 93, 183, Plate I. ISBN 978-1-56902-440-9.. The pages in this edition have numbers six less than the same pages in the original edition.
- ↑ Deckers, Michael (2003). "Cyclus Decemnovennalis Dionysii". http://hbar.phys.msu.ru/gorm/chrono/paschata.htm.
- ↑ C. W. Jones, ed., Opera Didascalica, vol. 123C in Corpus Christianorum, Series Latina.
- ↑ 30.0 30.1 Hodgkin, Luke (2005). A History of Mathematics: From Mesopotamia to Modernity. Oxford University Press. p. 85. ISBN 978-0-19-152383-0. https://archive.org/details/historyofmathema0000hodg.
- ↑ O'Connor, John J.; Robertson, Edmund F. (January 2004), "Chinese numerals", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/HistTopics/Chinese_numerals.html.
- ↑ Shen, Crossley & Lun 1999, p. 12: "the ancient Chinese system is a place notation system"
- ↑ Shen, Kangshen; Crossley, John N.; Lun, Anthony W.-C. (1999). The Nine Chapters on the Mathematical Art: Companion and Commentary. Oxford University Press. p. 35. ISBN 978-0-19-853936-0. https://books.google.com/books?id=eiTJHRGTG6YC. "zero was regarded as a number in India ... whereas the Chinese employed a vacant position"
- ↑ "Mathematics in the Near and Far East". p. 262. http://grmath4.phpnet.us/istoria/the_history_of%20math_greece/the_history_of%20math_greece_3-5.pdf.
- ↑ Martzloff, Jean-Claude (2007). A History of Chinese Mathematics. Springer. p. 208. ISBN 978-3-540-33783-6.
- ↑ Struik, Dirk J. (1987). A Concise History of Mathematics. New York: Dover Publications. pp. 32–33. "In these matrices we find negative numbers, which appear here for the first time in history."
- ↑ 37.0 37.1 Plofker, Kim (2009). Mathematics in India. Princeton University Press. pp. 54–56. ISBN 978-0-691-12067-6. "In the Chandah-sutra of Pingala, dating perhaps the third or second century BC, [ ...] Pingala's use of a zero symbol [śūnya] as a marker seems to be the first known explicit reference to zero. ... In the Chandah-sutra of Pingala, dating perhaps the third or second century BC, there are five questions concerning the possible meters for any value "n". [ ...] The answer is (2)7 = 128, as expected, but instead of seven doublings, the process (explained by the sutra) required only three doublings and two squarings – a handy time saver where "n" is large. Pingala's use of a zero symbol as a marker seems to be the first known explicit reference to zero"
- ↑ Vaman Shivaram Apte (1970). "Sanskrit Prosody and Important Literary and Geographical Names in the Ancient History of India". The Student's Sanskrit-English Dictionary. Motilal Banarsidass. pp. 648–649. ISBN 978-81-208-0045-8. https://books.google.com/books?id=4ArxvCxV1l4C&pg=PA648. Retrieved 21 April 2017.
- ↑ Hall, Rachel (February 15, 2005). "Math for Poets and Drummers: The Mathematics of Rhythm". Saint Joseph's University. http://people.sju.edu/~rhall/Rhythms/Poets/arcadia.pdf.
- ↑ Bourbaki 1998, p. 46
- ↑ Weiss, Ittay (20 September 2017). "Nothing matters: How India's invention of zero helped create modern mathematics". The Conversation. https://theconversation.com/nothing-matters-how-the-invention-of-zero-helped-create-modern-mathematics-84232.
- ↑ 42.0 42.1 Devlin, Hannah (13 September 2017). "Much ado about nothing: ancient Indian text contains earliest zero symbol". The Guardian. ISSN 0261-3077. https://www.theguardian.com/science/2017/sep/14/much-ado-about-nothing-ancient-indian-text-contains-earliest-zero-symbol.
- ↑ Revell, Timothy (14 September 2017). "History of zero pushed back 500 years by ancient Indian text". New Scientist. https://www.newscientist.com/article/2147450-history-of-zero-pushed-back-500-years-by-ancient-indian-text.
- ↑ "Carbon dating finds Bakhshali manuscript contains oldest recorded origins of the symbol 'zero'". Bodleian Library. 14 September 2017. http://www.bodleian.ox.ac.uk/bodley/news/2017/sep-14.
- ↑ Ifrah (2000), p. 416.
- ↑ Aryabhatiya of Aryabhata, translated by Walter Eugene Clark.
- ↑ J J O'Connor; E F Robertson (2000). "Aryabhata the Elder". http://www-history.mcs.st-andrews.ac.uk/Biographies/Aryabhata_I.html.
- ↑ William L. Hosch, ed (15 August 2010). The Britannica Guide to Numbers and Measurement (Math Explained). The Rosen Publishing Group. pp. 97–98. ISBN 978-1-61530-108-9. https://books.google.com/books?id=cuN7rH6RzikC&pg=PA97. Retrieved 26 September 2016.
- ↑ Algebra, with Arithmetic and Mensuration from the Sanscrit of Brahmegupta and Bháscara. London: John Murray. 1817. OCLC 1039515732. https://archive.org/details/algebrawitharith00brahuoft.
- ↑ Kaplan 2000, p. 68–75.
- ↑
- Cœdès, George (1931). "A propos de l'origine des chiffres arabes" (in fr). Bulletin of the School of Oriental Studies, University of London (Cambridge University Press) 6 (2): 323–328. doi:10.1017/S0041977X00092806.
- Diller, Anthony (1996). "New Zeros and Old Khmer". The Mon-Khmer Studies Journal 25: 125–132. http://sealang.net/sala/archives/pdf8/diller1996new.pdf.
- ↑ Casselman, Bill. "All for Nought". University of British Columbia), American Mathematical Society. http://www.ams.org/samplings/feature-column/fcarc-india-zero.
- ↑ Ifrah (2000), p. 400.
- ↑ Pannekoek, Anton (1961). A History of Astronomy. George Allen & Unwin. p. 165. ISBN 9780045200023. OCLC 840043.
- ↑ 55.0 55.1 55.2 Durant, Will (1950). The Story of Civilization. 4, The Age of Faith: Constantine to Dante – A.D. 325–1300. Simon & Schuster. ISBN 978-0-9650007-5-8. "The Arabic inheritance of science was overwhelmingly Greek, but Hindu influences ranked next. In 773, at Mansur's behest, translations were made of the Siddhantas – Indian astronomical treatises dating as far back as 425 BC; these versions may have the vehicle through which the "Arabic" numerals and the zero were brought from India into Islam. In 813, al-Khwarizmi used the Hindu numerals in his astronomical tables."
- ↑ Brezina, Corona (2006). Al-Khwarizmi: The Inventor of Algebra. The Rosen Publishing Group. ISBN 978-1-4042-0513-0. https://books.google.com/books?id=955jPgAACAAJ. Retrieved 26 September 2016.
- ↑ Durant 1950, p. 241: "In 976, Muhammad ibn Ahmad, in his Keys of the Sciences, remarked that if, in a calculation, no number appears in the place of tens, a little circle should be used "to keep the rows". This circle the Mosloems called ṣifr, "empty" whence our cipher."
- ↑
- Sigler, Laurence (2003). Fibonacci's Liber Abaci: A Translation into Modern English of Leonardo Pisano's Book of Calculation. Sources and Studies in the History of Mathematics and Physical Sciences. Springer. doi:10.1007/978-1-4613-0079-3. ISBN 978-1-4613-0079-3.
- Grimm, Richard E. (February 1973). "The Autobiography of Leonardo Pisano". Fibonacci Quarterly 11 (1): 99–104. https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=318a17253f745e2af400eb2ebb4dc4e762560a5b.
- Hansen, Alice (2008) (in en). Primary Mathematics: Extending Knowledge in Practice. SAGE. doi:10.4135/9781446276532. ISBN 978-0-85725-233-3. https://books.google.com/books?id=COJsbuUI1h8C&pg=PT31. Retrieved 7 November 2020.
- ↑ 59.0 59.1 Smith, D. E.; Karpinski, L. C. (1911). "The spread of the [Hindu–Arabic] numerals in Europe". The Hindu–Arabic Numerals. Ginn and Company. pp. 134–136. https://archive.org/stream/hinduarabicnume02karpgoog#page/n145/mode/1up.
- ↑ Pedersen, Olaf (1985). "In Quest of Sacrobosco". Journal for the History of Astronomy 16 (3): 175–221. doi:10.1177/002182868501600302. Bibcode: 1985JHA....16..175P.
- ↑ Ifrah 2000, pp. 588–590.
- ↑ 62.0 62.1 Bemer, R. W. (1967). "Towards standards for handwritten zero and oh: much ado about nothing (and a letter), or a partial dossier on distinguishing between handwritten zero and oh". Communications of the ACM 10 (8): 513–518. doi:10.1145/363534.363563.
- ↑ Reimer 2014, pp. 156,199–204.
- ↑ Bunt, Lucas Nicolaas Hendrik; Jones, Phillip S.; Bedient, Jack D. (1976). The historical roots of elementary mathematics. Courier Dover Publications. pp. 254–255. ISBN 978-0-486-13968-5. https://books.google.com/books?id=7xArILpcndYC. Retrieved 5 January 2016., Extract of pp. 254–255
- ↑ Cheng 2017, p. 32.
- ↑ Cheng 2017, pp. 41, 48–53.
- ↑ Weisstein, Eric W.. "Zero" (in en). http://mathworld.wolfram.com/Zero.html.
- ↑ Weil, André (2012-12-06) (in en). Number Theory for Beginners. Springer Science & Business Media. ISBN 978-1-4612-9957-8. https://books.google.com/books?id=NEHaBwAAQBAJ&pg=PA3. Retrieved 6 April 2021.
- ↑ Lemma B.2.2, The integer 0 is even and is not odd, in Penner, Robert C. (1999). Discrete Mathematics: Proof Techniques and Mathematical Structures. World Scientific. p. 34. ISBN 978-981-02-4088-2. https://archive.org/details/discretemathemat0000penn.
- ↑ Reid, Constance (1992). From zero to infinity: what makes numbers interesting (4th ed.). Mathematical Association of America. p. 23. ISBN 978-0-88385-505-8. "zero neither prime nor composite"
- ↑ Cheng 2017, p. 47.
- ↑ Herman, Edwin et al. (2017). Calculus. 1. Houston, Texas: OpenStax. pp. 454–459. ISBN 978-1-938168-02-4. OCLC 1022848630. https://openstax.org/details/books/calculus-volume-1. Retrieved 26 July 2022.
- ↑ Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1988). Concrete Mathematics. Reading, MA: Addison-Wesley. p. 111. ISBN 0-201-14236-8.
- ↑ Cheng 2017, p. 60.
- ↑ Kardar 2007, p. 35.
- ↑ Riehl, Emily (2016). Category Theory in Context. Dover. p. 103. ISBN 978-0-486-80903-8. https://math.jhu.edu/~eriehl/context/.
- ↑ Rex, Andrew; Finn, C. B. P. (2017). Finn's Thermal Physics (3rd ed.). CRC Press. pp. 8–16. ISBN 978-1-4987-1887-5.
- ↑ Kardar 2007, pp. 4–5,103–104.
- ↑ Woodford 2006, p. 9.
- ↑ Hill 2020, p. 20.
- ↑ "ResultSet (Java Platform SE 8 )". https://docs.oracle.com/javase/8/docs/api/java/sql/ResultSet.html.
- ↑ Reese, Richard M. (2013). Understanding and Using C Pointers: Core Techniques for Memory Management. O'Reilly Media. ISBN 978-1-449-34455-9. https://books.google.com/books?id=-U155tRMLJgC&dq=C%20%22null%20pointer%22%200&pg=PT26.
- ↑ Wu, X.; Ichikawa, T.; Cercone, N. (25 October 1996) (in en). Knowledge-Base Assisted Database Retrieval Systems. World Scientific. ISBN 978-981-4501-75-0. https://books.google.com/books?id=SdLsCgAAQBAJ&q=%C2%A0In+databases%2C+it+is+possible+for+a+field+not+to+have+a+value+%28null%29&pg=PT197. Retrieved 7 November 2020.
- ↑ "Null values and the nullable type". 12 December 2018. https://www.ibm.com/docs/en/rbd/9.5.1?topic=parts-null-values-nullable-type. "In regard to services, sending a null value as an argument in a remote service call means that no data is sent. Because the receiving parameter is nullable, the receiving function creates a new, uninitialized value for the missing data then passes it to the requested service function."
- ↑ Paul DuBois. "MySQL Cookbook: Solutions for Database Developers and Administrators" 2014. p. 204.
- ↑ Arnold Robbins; Nelson Beebe. "Classic Shell Scripting" . 2005. p. 274
- ↑ Iztok Fajfar. "Start Programming Using HTML, CSS, and JavaScript" . 2015. p. 160.
- ↑ Darren R. Hayes. "A Practical Guide to Computer Forensics Investigations" . 2014. p. 399
- ↑ "Font Survey: 42 of the Best Monospaced Programming Fonts". 18 August 2010. https://www.codeproject.com/Articles/30040/Font-Survey-42-of-the-Best-Monospaced-Programming.
- ↑ Cepelewicz, Jordana (August 9, 2021). "Animals Count and Use Zero. How Far Does Their Number Sense Go?". Quanta Magazine. https://www.quantamagazine.org/animals-can-count-and-use-zero-how-far-does-their-number-sense-go-20210809/.
- ↑ Steel, Duncan (2000). Marking Time: The epic quest to invent the perfect calendar. John Wiley & Sons. p. 113. ISBN 978-0-471-29827-4. OCLC 1135427740. https://archive.org/details/markingtimeepicq00stee_0/page/113. "In the B.C./A.D. scheme there is no year zero. After 31 December 1 BC came 1 January AD 1. ... If you object to that no-year-zero scheme, then don't use it: use the astronomer's counting scheme, with negative year numbers."
Bibliography
- Aczel, Amir D. (2015). Finding Zero. New York: Palgrave Macmillan. ISBN 978-1-137-27984-2. https://archive.org/details/findingzeromathe0000acze.
- Asimov, Isaac (1978). "Nothing Counts". Asimov on Numbers. New York: Pocket Books. ISBN 978-0-671-82134-0. OCLC 1105483009. https://archive.org/details/asimovonnumbers00isaa.
- Barrow, John D. (2001). The Book of Nothing. Vintage. ISBN 0-09-928845-1. https://archive.org/details/bookofnothing0000barr.
- Cheng, Eugenia (2017). Beyond Infinity: An Expedition to the Outer Limits of Mathematics. Basic Books. ISBN 978-1-5416-4413-7.
- Kardar, Mehran (2007). Statistical Physics of Particles. Cambridge University Press. ISBN 978-0-521-87342-0.
- Reimer, David (2014). Count Like an Egyptian. Princeton University Press. ISBN 978-0-691-16012-2.
- Woodford, Chris (2006). Digital Technology. Evans Brothers. ISBN 978-0-237-52725-9. https://books.google.com/books?id=My7Zr0aP2L8C&pg=PA9. Retrieved 24 March 2016.
- Hill, Christian (2020). Learning Scientific Programming with Python (2nd ed.). Cambridge University Press. ISBN 978-1-10707541-2.
Historical studies
- Bourbaki, Nicolas (1998). Elements of the History of Mathematics. Berlin, Heidelberg, and New York: Springer-Verlag. ISBN 3-540-64767-8.
- Diehl, Richard A. (2004). The Olmecs: America's First Civilization. London: Thames & Hudson. ISBN 978-0-500-28503-9.
- Ifrah, Georges (2000). The Universal History of Numbers: From Prehistory to the Invention of the Computer. Wiley. ISBN 0-471-39340-1.
- Kaplan, Robert (2000). The Nothing That Is: A Natural History of Zero. Oxford University Press. ISBN 978-0-198-02945-8.
- Seife, Charles (2000). Zero: The Biography of a Dangerous Idea. Penguin USA. ISBN 0-14-029647-6.
External links
- Searching for the World's First Zero
- A History of Zero
- Zero Saga
- The History of Algebra
- Edsger W. Dijkstra: Why numbering should start at zero, EWD831 (PDF of a handwritten manuscript)
- Weisstein, Eric W.. "0". http://mathworld.wolfram.com/0.html.
 Texts on Wikisource:
Texts on Wikisource:
- "Zero". Encyclopedia Americana. 1920.
 |