Physics:Experimental testing of time dilation

From HandWiki
Revision as of 02:57, 5 February 2024 by Gametune (talk | contribs) (fixing)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Tests of special relativity
Relation between the speed and the Lorentz factor γ (and hence the time dilation of moving clocks).

Time dilation as predicted by special relativity is often verified by means of particle lifetime experiments. According to special relativity, the rate of a clock C traveling between two synchronized laboratory clocks A and B, as seen by a laboratory observer, is slowed relative to the laboratory clock rates. Since any periodic process can be considered a clock, the lifetimes of unstable particles such as muons must also be affected, so that moving muons should have a longer lifetime than resting ones. A variety of experiments confirming this effect have been performed both in the atmosphere and in particle accelerators. Another type of time dilation experiments is the group of Ives–Stilwell experiments measuring the relativistic Doppler effect.

Atmospheric tests

Minkowski diagram
a) View in S
b) View in S′
c) Loedel diagram (In order to make the differences smaller, 0.7c was used instead of 0.995c)

Theory

The emergence of the muons is caused by the collision of cosmic rays with the upper atmosphere, after which the muons reach Earth. The probability that muons can reach the Earth depends on their half-life, which itself is modified by the relativistic corrections of two quantities: a) the mean lifetime of muons and b) the length between the upper and lower atmosphere (at Earth's surface). This allows for a direct application of length contraction upon the atmosphere at rest in inertial frame S, and time dilation upon the muons at rest in S′.[1][2]

Time dilation and length contraction

Length of the atmosphere: The contraction formula is given by [math]\displaystyle{ L=L_{0}/\gamma }[/math], where L0 is the proper length of the atmosphere and L its contracted length. As the atmosphere is at rest in S, we have γ=1 and its proper Length L0 is measured. As it is in motion in S′, we have γ>1 and its contracted length L′ is measured.

Decay time of muons: The time dilation formula is [math]\displaystyle{ T=\gamma \ T_{0} }[/math], where T0 is the proper time of a clock comoving with the muon, corresponding with the mean decay time of the muon in its proper frame. As the muon is at rest in S′, we have γ=1 and its proper time T′0 is measured. As it is moving in S, we have γ>1, therefore its proper time is shorter with respect to time T. (For comparison's sake, another muon at rest on Earth can be considered, called muon-S. Therefore, its decay time in S is shorter than that of muon-S′, while it is longer in S′.)

  • In S, muon-S′ has a longer decay time than muon-S. Therefore, muon-S' has sufficient time to pass the proper length of the atmosphere in order to reach Earth.
  • In S′, muon-S has a longer decay time than muon-S′. But this is no problem, since the atmosphere is contracted with respect to its proper length. Therefore, even the faster decay time of muon-S′ suffices in order to be passed by the moving atmosphere and to be reached by Earth.
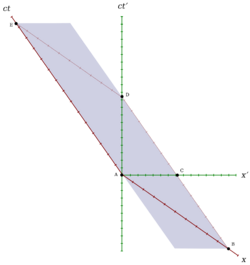
Minkowski diagram

The muon emerges at the origin (A) by collision of radiation with the upper atmosphere. The muon is at rest in S′, so its worldline is the ct′-axis. The upper atmosphere is at rest in S, so its worldline is the ct-axis. Upon the axes of x and x′, all events are present that are simultaneous with A in S and S′, respectively. The muon and Earth are meeting at D. As the Earth is at rest in S, its worldline (identical with the lower atmosphere) is drawn parallel to the ct-axis, until it intersects the axes of x′ and x.

Time: The interval between two events present on the worldline of a single clock is called proper time, an important invariant of special relativity. As the origin of the muon at A and the encounter with Earth at D is on the muon's worldline, only a clock comoving with the muon and thus resting in S′ can indicate the proper time T′0=AD. Due to its invariance, also in S it is agreed that this clock is indicating exactly that time between the events, and because it is in motion here, T′0=AD is shorter than time T indicated by clocks resting in S. This can be seen at the longer intervals T=BD=AE parallel to the ct-axis.

Length: Event B, where the worldline of Earth intersects the x-axis, corresponds in S to the position of Earth simultaneous with the emergence of the muon. C, where the Earth's worldline intersects the x′-axis, corresponds in S′ to the position of Earth simultaneous with the emergence of the muon. Length L0=AB in S is longer than length L′=AC in S′.

Experiments

Results of the Frisch–Smith experiment. Curves computed for [math]\displaystyle{ M_{\mathrm{Newton}} }[/math] and [math]\displaystyle{ M_{\mathrm{SR}} }[/math].

If no time dilation exists, then those muons should decay in the upper regions of the atmosphere, however, as a consequence of time dilation they are present in considerable amount also at much lower heights. The comparison of those amounts allows for the determination of the mean lifetime as well as the half-life of muons. [math]\displaystyle{ N }[/math] is the number of muons measured in the upper atmosphere, [math]\displaystyle{ M }[/math] at sea level, [math]\displaystyle{ Z }[/math] is the travel time in the rest frame of the Earth by which the muons traverse the distance between those regions, and [math]\displaystyle{ T_0 }[/math] is the mean proper lifetime of the muons:[3]

[math]\displaystyle{ \begin{align} M_{\mathrm{Newton}} & =N\exp\left[-Z/T_{0}\right]\\ M_{\mathrm{SR}} & =N\exp\left[-Z/\left(\gamma T_{0}\right)\right] \end{align} }[/math]

Rossi–Hall experiment

In 1940 at Echo Lake (3240 m) and Denver in Colorado (1616 m), Bruno Rossi and D. B. Hall measured the relativistic decay of muons (which they thought were mesons). They measured muons in the atmosphere traveling above 0.99 c (c being the speed of light). Rossi and Hall confirmed the formulas for relativistic momentum and time dilation in a qualitative manner. Knowing the momentum and lifetime of moving muons enabled them to compute their mean proper lifetime too – they obtained ≈ 2.4 μs (modern experiments improved this result to ≈ 2.2 μs).[4][5][6][7]

Frisch–Smith experiment

A much more precise experiment of this kind was conducted by David H. Frisch and Smith (1962) and documented by a film.[8] They measured approximately 563 muons per hour in six runs on Mount Washington at 1917m above sea-level. By measuring their kinetic energy, mean muon velocities between 0.995 c and 0.9954 c were determined. Another measurement was taken in Cambridge, Massachusetts at sea-level. The time the muons need from 1917m to 0m should be about 6.4 μs. Assuming a mean lifetime of 2.2 μs, only 27 muons would reach this location if there were no time dilation. However, approximately 412 muons per hour arrived in Cambridge, resulting in a time dilation factor of 8.8±0.8.

Frisch and Smith showed that this is in agreement with the predictions of special relativity: The time dilation factor for muons on Mount Washington traveling at 0.995 c to 0.9954 c is approximately 10.2. Their kinetic energy and thus their velocity was diminished until they reached Cambridge to 0.9881 c and 0.9897 c due to the interaction with the atmosphere, reducing the dilation factor to 6.8. So between the start (≈ 10.2) and the target (≈ 6.8) an average time dilation factor of 8.4±2 was determined by them, in agreement with the measured result within the margin of errors (see the above formulas and the image for computing the decay curves).[9]

Other experiments

Since then, many measurements of the mean lifetime of muons in the atmosphere and time dilation have been conducted in undergraduate experiments.[3][10]

Accelerator and atomic clock tests

Time dilation and CPT symmetry

Much more precise measurements of particle decays have been made in particle accelerators using muons and different types of particles. Besides the confirmation of time dilation, also CPT symmetry was confirmed by comparing the lifetimes of positive and negative particles. This symmetry requires that the decay rates of particles and their antiparticles have to be the same. A violation of CPT invariance would also lead to violations of Lorentz invariance and thus special relativity.

Pion Kaon Muon
Durbin et al. (1952)[11]

Eckhause et al. (1965)[12]

Nordberg et al. (1967)[13]

Greenburg et al. (1969)[14]

Ayres et al. (1971)[15]

Burrowes et al. (1959)[16]

Nordin (1961)[17]

Boyarski et al. (1962)[18]

Lobkowicz et al. (1969)[19]

Ott et al. (1971)[20]

Skjeggestad et al. (1971)[21]

Geweniger et al. (1974)[22]

Carithers et al. (1975)[23]

Lundy (1962)[24]

Meyer et al. (1963)[25]

Eckhause et al. (1963)[26]

Balandin et al. (1974)[27]

Today, time dilation of particles is routinely confirmed in particle accelerators along with tests of relativistic energy and momentum, and its consideration is obligatory in the analysis of particle experiments at relativistic velocities.

Twin paradox and moving clocks

Bailey et al. (1977) measured the lifetime of positive and negative muons sent around a loop in the CERN Muon storage ring. This experiment confirmed both time dilation and the twin paradox, i.e. the hypothesis that clocks sent away and coming back to their initial position are slowed with respect to a resting clock.[28][29] Other measurements of the twin paradox involve gravitational time dilation as well.

In the Hafele–Keating experiment, actual cesium-beam atomic clocks were flown around the world and the expected differences were found compared to a stationary clock.

Clock hypothesis - lack of effect of acceleration

The clock hypothesis states that the extent of acceleration does not influence the value of time dilation. In most of the former experiments mentioned above, the decaying particles were in an inertial frame, i.e. unaccelerated. However, in Bailey et al. (1977) the particles were subject to a transverse acceleration of up to ~1018 g. Since the result was the same, it was shown that acceleration has no impact on time dilation.[28] In addition, Roos et al. (1980) measured the decay of Sigma baryons, which were subject to a longitudinal acceleration between 0.5 and 5.0 × 1015 g. Again, no deviation from ordinary time dilation was measured.[30]

See also

References

  1. ↑ Leo Sartori (1996), Understanding Relativity: a simplified approach to Einstein's theories, University of California Press, ISBN:0-520-20029-2, p 9
  2. ↑ Sexl, Roman; Schmidt, Herbert K. (1979). Raum-Zeit-Relativität. Braunschweig: Vieweg. ISBN 3528172363. 
  3. ↑ 3.0 3.1 Easwar, Nalini; Macintire, Douglas A. (1991). "Study of the effect of relativistic time dilation on cosmic ray muon flux – An undergraduate modern physics experiment". American Journal of Physics 59 (7): 589–592. doi:10.1119/1.16841. Bibcode: 1991AmJPh..59..589E. https://scholarworks.smith.edu/cgi/viewcontent.cgi?article=1041&context=phy_facpubs. 
  4. ↑ Rossi, B.; Hall, D. B. (1941). "Variation of the Rate of Decay of Mesotrons with Momentum". Physical Review 59 (3): 223–228. doi:10.1103/PhysRev.59.223. Bibcode: 1941PhRv...59..223R. 
  5. ↑ Rossi, B.; Greisen, K.; Stearns, J. C.; Froman, D. K.; Koontz, P. G. (1942). "Further Measurements of the Mesotron Lifetime". Physical Review 61 (11–12): 675–679. doi:10.1103/PhysRev.61.675. Bibcode: 1942PhRv...61..675R. 
  6. ↑ Rossi, B.; Nereson, N. (1942). "Experimental Determination of the Disintegration Curve of Mesotrons". Physical Review 62 (9–10): 417–422. doi:10.1103/PhysRev.62.417. Bibcode: 1942PhRv...62..417R. 
  7. ↑ Rossi, B.; Nereson, N. (1943). "Further Measurements on the Disintegration Curve of Mesotrons". Physical Review 64 (7–8): 199–201. doi:10.1103/PhysRev.64.199. Bibcode: 1943PhRv...64..199N. 
  8. ↑ "Time Dilation, An Experiment With Mu - Mesons (1962)". The Science Teaching Center, MIT. https://www.youtube.com/watch?v=5wH2UbjGKlw. Retrieved 20 February 2022. 
  9. ↑ Frisch, D. H.; Smith, J. H. (1963). "Measurement of the Relativistic Time Dilation Using μ-Mesons". American Journal of Physics 31 (5): 342–355. doi:10.1119/1.1969508. Bibcode: 1963AmJPh..31..342F. 
  10. ↑ Coan, Thomas; Liu, Tiankuan; Ye, Jingbo (2006). "A Compact Apparatus for Muon Lifetime Measurement and Time Dilation Demonstration in the Undergraduate Laboratory". American Journal of Physics 74 (2): 161–164. doi:10.1119/1.2135319. Bibcode: 2006AmJPh..74..161C. 
  11. ↑ Durbin, R. P.; Loar, H. H.; Havens, W. W. (1952). "The Lifetimes of the π+ and π−Mesons". Physical Review 88 (2): 179–183. doi:10.1103/PhysRev.88.179. Bibcode: 1952PhRv...88..179D. 
  12. ↑ Eckhause, M.; Harris, R. J., Jr.; Shuler, W. B.; Siegel, R. T.; Welsh, R. E. (1967). "Remeasurement of the π+ lifetime". Physics Letters 19 (4): 348–350. doi:10.1016/0031-9163(65)91016-4. Bibcode: 1965PhL....19..348E. 
  13. ↑ Nordberg, M. E.; Lobkowicz, F.; Burman, R. L. (1967). "Remeasurement of the π+ lifetime". Physics Letters B 24 (11): 594–596. doi:10.1016/0370-2693(67)90401-7. Bibcode: 1967PhLB...24..594N. 
  14. ↑ Greenberg, A. J.; Ayres, D. S.; Cormack, A. M.; Kenney, R. W.; Caldwell, D. O.; Elings, V. B.; Hesse, W. P.; Morrison, R. J. (1969). "Charged-Pion Lifetime and a Limit on a Fundamental Length". Physical Review Letters 23 (21): 1267–1270. doi:10.1103/PhysRevLett.23.1267. Bibcode: 1969PhRvL..23.1267G. http://www.escholarship.org/uc/item/99m3048v. 
  15. ↑ Ayres, D. S.; Cormack, A. M.; Greenberg, A. J.; Kenney, R. W.; Caldwell, D. O.; Elings, V. B.; Hesse, W. P.; Morrison, R. J. (1971). "Measurements of the Lifetimes of Positive and Negative Pions". Physical Review D 3 (5): 1051–1063. doi:10.1103/PhysRevD.3.1051. Bibcode: 1971PhRvD...3.1051A. https://escholarship.org/uc/item/8ct8s1sp. 
  16. ↑ Burrowes, H. C.; Caldwell, D. O.; Frisch, D. H.; Hill, D. A.; Ritson, D. M.; Schluter, R. A. (1959). "K-Meson-Nucleon Total Cross Sections from 0.6 to 2.0 Bev". Physical Review Letters 2 (3): 117–119. doi:10.1103/PhysRevLett.2.117. Bibcode: 1959PhRvL...2..117B. 
  17. ↑ Nordin, Paul (1961). "S- and P-Wave Interactions of K- Mesons in Hydrogen". Physical Review 123 (6): 2168–2176. doi:10.1103/PhysRev.123.2168. Bibcode: 1961PhRv..123.2168N. 
  18. ↑ Boyarski, A. M.; Loh, E. C.; Niemela, L. Q.; Ritson, D. M.; Weinstein, R.; Ozaki, S. (1962). "Study of the K+ Decay". Physical Review 128 (5): 2398–2402. doi:10.1103/PhysRev.128.2398. Bibcode: 1962PhRv..128.2398B. 
  19. ↑ Lobkowicz, F.; Melissinos, A. C.; Nagashima, Y.; Tewksbury, S.; von Briesen, H.; Fox, J. D. (1969). "Precise Measurement of the K+K- Lifetime Ratio". Physical Review 185 (5): 1676–1686. doi:10.1103/PhysRev.185.1676. Bibcode: 1969PhRv..185.1676L. 
  20. ↑ Ott, R. J.; Pritchard, T. W. (1971). "Precise Measurement of the K+ Lifetime". Physical Review D 3 (1): 52–56. doi:10.1103/PhysRevD.3.52. Bibcode: 1971PhRvD...3...52O. 
  21. ↑ Skjeggestad, O.; James, F.; Montanet, L.; Paul, E.; Saetre, P.; Sendall, D. M.; Burgun, G.; Lesquoy, E. et al. (1972). "Measurement of the KSO mean life". Nuclear Physics B 48 (2): 343–352. doi:10.1016/0550-3213(72)90174-5. Bibcode: 1972NuPhB..48..343S. 
  22. ↑ Geweniger, C.; Gjesdal, S.; Presser, G.; Steffen, P.; Steinberger, J.; Vannucci, F.; Wahl, H.; Eisele, F. et al. (1974). "A new determination of the Ko --> π+π- decay parameters". Physics Letters B 48 (5): 487–491. doi:10.1016/0370-2693(74)90385-2. Bibcode: 1974PhLB...48..487G. 
  23. ↑ Carithers, W. C.; Modis, T.; Nygren, D. R.; Pun, T. P.; Schwartz, E. L.; Sticker, H.; Christenson, J. H. (1975). "Measurement of the Phase of the CP-Nonconservation Parameter η+- and the KS Total Decay Rate". Physical Review Letters 34 (19): 1244–1246. doi:10.1103/PhysRevLett.34.1244. Bibcode: 1975PhRvL..34.1244C. 
  24. ↑ Lundy, R. A. (1962). "Precision Measurement of the μ+ Lifetime". Physical Review 125 (5): 1686–1696. doi:10.1103/PhysRev.125.1686. Bibcode: 1962PhRv..125.1686L. 
  25. ↑ Meyer, S. L.; Anderson, E. W.; Bleser, E.; Lederman, I. M.; Rosen, J. L.; Rothberg, J.; Wang, I.-T. (1963). "Precision Lifetime Measurements on Positive and Negative Muons". Physical Review 132 (6): 2693–2698. doi:10.1103/PhysRev.132.2693. Bibcode: 1963PhRv..132.2693M. 
  26. ↑ Eckhause, M.; Filippas, T. A.; Sutton, R. B.; Welsh, R. E. (1963). "Measurements of Negative-Muon Lifetimes in Light Isotopes". Physical Review 132 (1): 422–425. doi:10.1103/PhysRev.132.422. Bibcode: 1963PhRv..132..422E. https://digital.library.unt.edu/ark:/67531/metadc1463169/. 
  27. ↑ Balandin, M. P.; Grebenyuk, V. M.; Zinov, V. G.; Konin, A. D.; Ponomarev, A. N. (1974). "Measurement of the lifetime of the positive muon". Soviet Physics JETP 40: 811. Bibcode: 1975JETP...40..811B. 
  28. ↑ 28.0 28.1 Bailey, H.; Borer, K.; Combley F.; Drumm H.; Krienen F.; Lange F.; Picasso E.; Ruden W. von et al. (1977). "Measurements of relativistic time dilatation for positive and negative muons in a circular orbit". Nature 268 (5618): 301–305. doi:10.1038/268301a0. Bibcode: 1977Natur.268..301B. 
  29. ↑ Bailey, J.; Borer, K.; Combley, F.; Drumm, H.; Eck, C.; Farley, F. J. M.; Field, J. H.; Flegel, W. et al. (1979). "Final report on the CERN muon storage ring including the anomalous magnetic moment and the electric dipole moment of the muon, and a direct test of relativistic time dilation". Nuclear Physics B 150: 1–75. doi:10.1016/0550-3213(79)90292-X. Bibcode: 1979NuPhB.150....1B. https://cds.cern.ch/record/133132. 
  30. ↑ Roos, C. E.; Marraffino, J.; Reucroft, S.; Waters, J.; Webster, M. S.; Williams, E. G. H. (1980). "σ+/- lifetimes and longitudinal acceleration". Nature 286 (5770): 244–245. doi:10.1038/286244a0. Bibcode: 1980Natur.286..244R. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Experimental_testing_of_time_dilation&oldid=3276924"