Physics:History of field theory
In the history of physics, the concept of fields had its origins in the 18th century in a mathematical formulation of Newton's law of universal gravitation, but it was seen as deficient as it implied action at a distance. In 1852, Michael Faraday treated the magnetic field as a physical object, reasoning about lines of force. James Clerk Maxwell used Faraday's conceptualisation to help formulate his unification of electricity and magnetism in his theory of electromagnetism.
With Albert Einstein's special relativity and the Michelson–Morley experiment, it became clear that electromagnetic waves could travel in vacuum without the need of a medium or luminiferous aether. Einstein also developed general relativity, in which spacetime was treated as a field and its curvature was the origin of the gravitational interactions, putting an end to action at a distance.
In quantum field theory, fields become the fundamental objects of study, and particles are excitations of these fields.
Inverse square laws
The formal definition of gravitational force was introduced by Newton's law of universal gravitation. The success of Newtonian physics since the publication of Isaac Newton's Principia in 1687 provided a framework with which to investigate the motion and forces associated with electricity and magnetism. Charles-Augustin de Coulomb showed in 1785 that the repulsive force between two electrically charged spheres obeys the same (up to a sign) force law as Newton's law of universal gravitation: the force between two bodies is directed along the line separating the bodies and its magnitude is proportional to the product of their charges (for gravitation, their masses) divided by the square of their distance apart. André-Marie Ampère showed in 1823 that the force between infinitesimal lengths of current-carrying wires similarly obeys an inverse-square law such that the force is directed along the line of separation between the wire elements.[1]
Despite the success of these theories in making accurate numerical predictions of a wide range of phenomena, these laws were generally seen as deficient as natural philosophies of mechanics, since they were all essentially action-at-a-distance mechanisms. In the context of the development of field theory, the fact that a function could be written to give the force per unit mass, charge, or current for each point in space was just a mathematical construct. It was seen as untenable on metaphysical grounds[2][3] that a force be exerted across empty space, and hence these force laws were assumed to be merely descriptive and not explanatory.
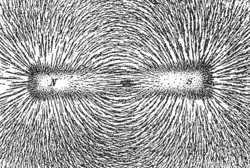
Introduction of fields in electricity and magnetism

Michael Faraday coined the term "magnetic field" in his Researches when postulating, after discovering that all the constituent materials of a human are diamagnetic, that if a human were set in a sufficiently strong magnetic field then they too would align with the field. Faraday did not conceive of this field as a mere mathematical construct for calculating the forces between particles—having only rudimentary mathematical training, he had no use for abstracting reality to make quantitative predictions.[1] Instead he conjectured that there was force filling the space where electromagnetic fields were generated and reasoned qualitatively about these forces with force lines:
"Important to the definition of these lines is that they represent a determinate and unchanging amount of force. Though, therefore, their forms, as they exist between two or more centers or sources of power, may vary greatly, and also the space through which they may be traced, yet the sum of power contained in any one section of a given portion of the lines is exactly equal to the sum of power in any other section of the same lines, however altered in form or however convergent or divergent they may be at the second place."[4]
Faraday's insights into the behavior of magnetic fields would prove invaluable for the development of electromagnetism, in terms of the relations between magnetic and electric fields. In 1865, James Clerk Maxwell compiled all known equations of electromagnetism. Maxwell's equations together led to a wave equation that propagated at the speed of light. Thus explaining electromagnetic radiation in terms of the same electric and magnetic fields. In order to explain this wave phenomena, Maxwell considered a luminiferous aether, a medium tha permeated all space that allowed light to propagate. He wrote
"Another theory of electricity which I prefer denies action at a distance and attributes electric action to tensions and pressures in an all-pervading medium, these stresses being the same in kind with those familiar to engineers, and the medium being identical with that in which light is supposed to be propagated."[5]
Relativity
The Michelson–Morley experiment attempted to prove that electromagnetic radiation were oscillations of a luminiferous aether, however the result was negative, indicating that radiation could travel in vacuum. To explain this phenomenon, Albert Einstein developed his theory of special relativity (1905) which resolved the conflicts between classical mechanics and electromagnetism.
Einstein also developed general relativity in 1915, consistent with special relativity and that could explain gravitation in terms of a field theory of spacetime.
Quantum fields
Fields become the fundamental object of study in quantum field theory. Mathematically, quantum fields are formalized as operator-valued distributions.[6] Although there is no direct method of measuring the fields themselves, the framework asserts that all particles are "excitations" of these fields. For example: whereas Maxwell's theory of classical electromagnetism describes light as a self-propagating wave in the electromagnetic field, in quantum electrodynamics light is the massless gauge boson particle called the photon. Furthermore, the number of particles in an isolated system need not be conserved; an example of a process for which this is the case is bremsstrahlung. More detailed understanding of the framework is obtained by studying the Lagrangian density of a field theory which encodes the information of its allowed particle interactions.[7]
References
- ↑ 1.0 1.1 Forbes, Nancy (2014). Faraday, Maxwell, and the Electromagnetic Field: How Two Men Revolutionized Physics. Amherst, NY: Prometheus Press. ISBN 978-1616149420.
- ↑ McMullin, Ernan. "The Origins of the Field Concept in Physics."
- ↑ Williams, Leslie Pearce (1966). The Origins of Field Theory. New York, NY: Random House. https://archive.org/details/originsoffieldth0000unse.
- ↑ Faraday, Michael. "Experimental Researches in Electricity.--Twenty-Eighth Series." Philosophical Transactions of the Royal Society of London 142 (1852): 25-56. JSTOR 108532.
- ↑ Dyson, Freeman. "Why is Maxwell's Theory so hard to understand?". http://www.damtp.cam.ac.uk/user/tong/em/dyson.pdf.
- ↑ Wald, Robert M. (2006-08-03). "The History and Present Status of Quantum Field Theory in Curved Spacetime". arXiv:gr-qc/0608018.
- ↑ V., Schroeder, Daniel (1995). An introduction to quantum field theory. Addison-Wesley. ISBN 9780201503975. OCLC 20393204. https://archive.org/details/introductiontoqu0000pesk.
 |