Physics:Newton's law of universal gravitation
| Part of a series on |
| Classical mechanics |
|---|
Newton's law of universal gravitation says that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. Separated objects attract and are attracted as if all their mass were concentrated at their centers. The publication of the law has become known as the "first great unification", as it marked the unification of the previously described phenomena of gravity on Earth with known astronomical behaviors.[1][2][3]
This is a general physical law derived from empirical observations by what Isaac Newton called inductive reasoning.[4] It is a part of classical mechanics and was formulated in Newton's work Philosophiæ Naturalis Principia Mathematica ("the Principia"), first published on 5 July 1687.
The equation for universal gravitation thus takes the form:
where F is the gravitational force acting between two objects, m1 and m2 are the masses of the objects, r is the distance between the centers of their masses, and G is the gravitational constant.
The first test of Newton's law of gravitation between masses in the laboratory was the Cavendish experiment conducted by the United Kingdom scientist Henry Cavendish in 1798.[5] It took place 111 years after the publication of Newton's Principia and approximately 71 years after his death.
Newton's law of gravitation resembles Coulomb's law of electrical forces, which is used to calculate the magnitude of the electrical force arising between two charged bodies. Both are inverse-square laws, where force is inversely proportional to the square of the distance between the bodies. Coulomb's law has charge in place of mass and a different constant.
Newton's law has later been superseded by Albert Einstein's theory of general relativity, but the universality of the gravitational constant is intact and the law still continues to be used as an excellent approximation of the effects of gravity in most applications. Relativity is required only when there is a need for extreme accuracy, or when dealing with very strong gravitational fields, such as those found near extremely massive and dense objects, or at small distances (such as Mercury's orbit around the Sun).
History
Around 1600, the scientific method began to take root. René Descartes started over with a more fundamental view, developing ideas of matter and action independent of theology. Galileo Galilei wrote about experimental measurements of falling and rolling objects. Johannes Kepler's laws of planetary motion summarized Tycho Brahe's astronomical observations.[6]:132
Around 1666 Isaac Newton developed the idea that Kepler's laws must also apply to the orbit of the Moon around the Earth and then to all objects on Earth. The analysis required assuming that the gravitation force acted as if all of the mass of the Earth were concentrated at its center, an unproven conjecture at that time. His calculations of the Moon orbit time was within 16% of the known value. By 1680, new values for the diameter of the Earth improved his orbit time to within 1.6%, but more importantly Newton had found a proof of his earlier conjecture.[7]:201
In 1687 Newton published his Principia which combined his laws of motion with new mathematical analysis to explain Kepler's empirical results.[6]:134 His explanation was in the form of a law of universal gravitation: any two bodies are attracted by a force proportional to their mass and inversely proportional to their separation squared.[8]:28 Newton's original formula was:
where the symbol means "is proportional to". To make this into an equal-sided formula or equation, there needed to be a multiplying factor or constant that would give the correct force of gravity no matter the value of the masses or distance between them (the gravitational constant). Newton would need an accurate measure of this constant to prove his inverse-square law. (When Newton presented Book 1 of the unpublished text in April 1686 to the Royal Society, Robert Hooke made a claim that Newton had obtained the inverse square law from him, ultimately a frivolous accusation[7]:204)
Newton's "causes hitherto unknown"
While Newton was able to formulate his law of gravity in his monumental work, he was deeply uncomfortable with the notion of "action at a distance" that his equations implied. In 1692, in his third letter to Bentley, he wrote: "That one body may act upon another at a distance through a vacuum without the mediation of anything else, by and through which their action and force may be conveyed from one another, is to me so great an absurdity that, I believe, no man who has in philosophic matters a competent faculty of thinking could ever fall into it."
He never, in his words, "assigned the cause of this power". In all other cases, he used the phenomenon of motion to explain the origin of various forces acting on bodies, but in the case of gravity, he was unable to experimentally identify the motion that produces the force of gravity (although he invented two mechanical hypotheses in 1675 and 1717). Moreover, he refused to even offer a hypothesis as to the cause of this force on grounds that to do so was contrary to sound science. He lamented that "philosophers have hitherto attempted the search of nature in vain" for the source of the gravitational force, as he was convinced "by many reasons" that there were "causes hitherto unknown" that were fundamental to all the "phenomena of nature". These fundamental phenomena are still under investigation and, though hypotheses abound, the definitive answer has yet to be found. And in Newton's 1713 General Scholium in the second edition of Principia: "I have not yet been able to discover the cause of these properties of gravity from phenomena and I feign no hypotheses.... It is enough that gravity does really exist and acts according to the laws I have explained, and that it abundantly serves to account for all the motions of celestial bodies."[9]
Modern form
In modern language, the law states the following:
| Every point mass attracts every single other point mass by a force acting along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them:[10] | 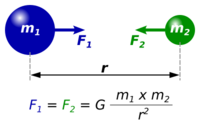 |
|
where
|

Assuming SI units, F is measured in newtons (N), m1 and m2 in kilograms (kg), r in meters (m), and the constant G is 6.67430(15)×10−11 m3⋅kg−1⋅s−2.[11] The value of the constant G was first accurately determined from the results of the Cavendish experiment conducted by the United Kingdom scientist Henry Cavendish in 1798, although Cavendish did not himself calculate a numerical value for G.[5] This experiment was also the first test of Newton's theory of gravitation between masses in the laboratory. It took place 111 years after the publication of Newton's Principia and 71 years after Newton's death, so none of Newton's calculations could use the value of G; instead he could only calculate a force relative to another force.
Bodies with spatial extent

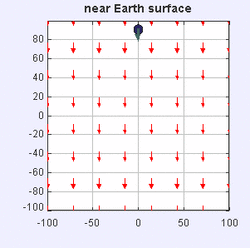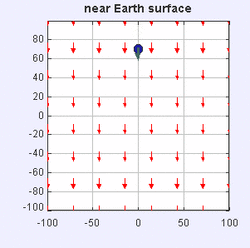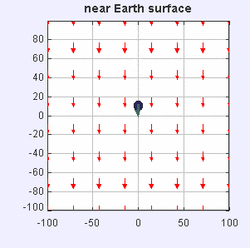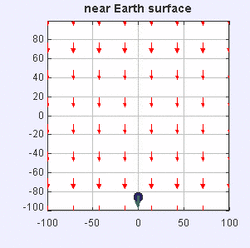
If the bodies in question have spatial extent (as opposed to being point masses), then the gravitational force between them is calculated by summing the contributions of the notional point masses that constitute the bodies. In the limit, as the component point masses become "infinitely small", this entails integrating the force (in vector form, see below) over the extents of the two bodies.
In this way, it can be shown that an object with a spherically symmetric distribution of mass exerts the same gravitational attraction on external bodies as if all the object's mass were concentrated at a point at its center.[10] (This is not generally true for non-spherically symmetrical bodies.)
For points inside a spherically symmetric distribution of matter, Newton's shell theorem can be used to find the gravitational force. The theorem tells us how different parts of the mass distribution affect the gravitational force measured at a point located a distance r0 from the center of the mass distribution:[12]
- The portion of the mass that is located at radii r < r0 causes the same force at the radius r0 as if all of the mass enclosed within a sphere of radius r0 was concentrated at the center of the mass distribution (as noted above).
- The portion of the mass that is located at radii r > r0 exerts no net gravitational force at the radius r0 from the center. That is, the individual gravitational forces exerted on a point at radius r0 by the elements of the mass outside the radius r0 cancel each other.
As a consequence, for example, within a shell of uniform thickness and density there is no net gravitational acceleration anywhere within the hollow sphere.
Vector form

Newton's law of universal gravitation can be written as a vector equation to account for the direction of the gravitational force as well as its magnitude. In this formula, quantities in bold represent vectors.
where
- F21 is the force applied on body 2 exerted by body 1,
- G is the gravitational constant,
- m1 and m2 are respectively the masses of bodies 1 and 2,
- r21 = r2 − r1 is the displacement vector between bodies 1 and 2, and
- is the unit vector from body 1 to body 2.[13]
It can be seen that the vector form of the equation is the same as the scalar form given earlier, except that F is now a vector quantity, and the right hand side is multiplied by the appropriate unit vector. Also, it can be seen that F12 = −F21.
Gravity field
The gravitational field is a vector field that describes the gravitational force that would be applied on an object in any given point in space, per unit mass. It is actually equal to the gravitational acceleration at that point.
It is a generalisation of the vector form, which becomes particularly useful if more than two objects are involved (such as a rocket between the Earth and the Moon). For two objects (e.g. object 2 is a rocket, object 1 the Earth), we simply write r instead of r12 and m instead of m2 and define the gravitational field g(r) as:
so that we can write:
This formulation is dependent on the objects causing the field. The field has units of acceleration; in SI, this is m/s2.
Gravitational fields are also conservative; that is, the work done by gravity from one position to another is path-independent. This has the consequence that there exists a gravitational potential field V(r) such that
If m1 is a point mass or the mass of a sphere with homogeneous mass distribution, the force field g(r) outside the sphere is isotropic, i.e., depends only on the distance r from the center of the sphere. In that case
the gravitational field is on, inside and outside of symmetric masses.
As per Gauss's law, field in a symmetric body can be found by the mathematical equation:
where is a closed surface and is the mass enclosed by the surface.
Hence, for a hollow sphere of radius and total mass ,
For a uniform solid sphere of radius and total mass ,
Limitations
Newton's description of gravity is sufficiently accurate for many practical purposes and is therefore widely used. Deviations from it are small when the dimensionless quantities and are both much less than one, where is the gravitational potential, is the velocity of the objects being studied, and is the speed of light in vacuum.[14] For example, Newtonian gravity provides an accurate description of the Earth/Sun system, since
where is the radius of the Earth's orbit around the Sun.
In situations where either dimensionless parameter is large, then general relativity must be used to describe the system. General relativity reduces to Newtonian gravity in the limit of small potential and low velocities, so Newton's law of gravitation is often said to be the low-gravity limit of general relativity.
Observations conflicting with Newton's formula
- Newton's theory does not fully explain the precession of the perihelion of the orbits of the planets, especially that of Mercury, which was detected long after the life of Newton.[15] There is a 43 arcsecond per century discrepancy between the Newtonian calculation, which arises only from the gravitational attractions from the other planets, and the observed precession, made with advanced telescopes during the 19th century.
- The predicted angular deflection of light rays by gravity (treated as particles travelling at the expected speed) that is calculated by using Newton's theory is only one-half of the deflection that is observed by astronomers.[citation needed] Calculations using general relativity are in much closer agreement with the astronomical observations.
- In spiral galaxies, the orbiting of stars around their centers seems to strongly disobey both Newton's law of universal gravitation and general relativity. Astrophysicists, however, explain this marked phenomenon by assuming the presence of large amounts of dark matter.
Einstein's solution
| Part of a series on |
| Spacetime |
|---|
 |
|
Special relativity General relativity |
The first two conflicts with observations above were explained by Einstein's theory of general relativity, in which gravitation is a manifestation of curved spacetime instead of being due to a force propagated between bodies. In Einstein's theory, energy and momentum distort spacetime in their vicinity, and other particles move in trajectories determined by the geometry of spacetime. This allowed a description of the motions of light and mass that was consistent with all available observations. In general relativity, the gravitational force is a fictitious force resulting from the curvature of spacetime, because the gravitational acceleration of a body in free fall is due to its world line being a geodesic of spacetime.
Extensions
In recent years, quests for non-inverse square terms in the law of gravity have been carried out by neutron interferometry.[16]
Solutions of Newton's law of universal gravitation
The n-body problem is an ancient, classical problem[17] of predicting the individual motions of a group of celestial objects interacting with each other gravitationally. Solving this problem — from the time of the Greeks and on — has been motivated by the desire to understand the motions of the Sun, planets and the visible stars. In the 20th century, understanding the dynamics of globular cluster star systems became an important n-body problem too.[18] The n-body problem in general relativity is considerably more difficult to solve.
The classical physical problem can be informally stated as: given the quasi-steady orbital properties (instantaneous position, velocity and time)[19] of a group of celestial bodies, predict their interactive forces; and consequently, predict their true orbital motions for all future times.[20]
The two-body problem has been completely solved, as has the restricted three-body problem.[21]
See also
- Bentley's paradox
- Gauss's law for gravity
- Jordan and Einstein frames
- Kepler orbit
- Newton's cannonball
- Newton's laws of motion
- Social gravity
- Static forces and virtual-particle exchange
Notes
References
- ↑ Fritz Rohrlich (25 August 1989). From Paradox to Reality: Our Basic Concepts of the Physical World. Cambridge University Press. pp. 28–. ISBN 978-0-521-37605-1. https://books.google.com/books?id=3TqA1394OVcC&pg=PA28.
- ↑ Klaus Mainzer (2 December 2013). Symmetries of Nature: A Handbook for Philosophy of Nature and Science. Walter de Gruyter. pp. 8–. ISBN 978-3-11-088693-1. https://books.google.com/books?id=QekhAAAAQBAJ&pg=PA8.
- ↑ "Physics: Fundamental Forces and the Synthesis of Theory | Encyclopedia.com". https://www.encyclopedia.com/science/science-magazines/physics-fundamental-forces-and-synthesis-theory.
- ↑ Isaac Newton: "In [experimental] philosophy particular propositions are inferred from the phenomena and afterwards rendered general by induction": "Principia", Book 3, General Scholium, at p.392 in Volume 2 of Andrew Motte's English translation published 1729.
- ↑ 5.0 5.1 The Michell–Cavendish Experiment, Laurent Hodges
- ↑ 6.0 6.1 Hesse, Mary B. (2005). Forces and fields: the concept of action at a distance in the history of physics (Dover ed.). Mineola, N.Y: Dover Publications. ISBN 978-0-486-44240-2.
- ↑ 7.0 7.1 Feather, Norman (1959). An Introduction to the Physics of Mass Length and Time. Edinburgh University Press.
- ↑ Whittaker, Edmund T. (1989). A history of the theories of aether & electricity. 1: The classical theories (Repr ed.). New York: Dover Publ. ISBN 978-0-486-26126-3.
- ↑ The Construction of Modern Science: Mechanisms and Mechanics, by Richard S. Westfall. Cambridge University Press. 1978
- ↑ 10.0 10.1 Proposition 75, Theorem 35: p. 956 – I.Bernard Cohen and Anne Whitman, translators: Isaac Newton, The Principia: Mathematical Principles of Natural Philosophy. Preceded by A Guide to Newton's Principia, by I.Bernard Cohen. University of California Press 1999 ISBN:0-520-08816-6 ISBN:0-520-08817-4
- ↑ "2018 CODATA Value: Newtonian constant of gravitation". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. http://physics.nist.gov/cgi-bin/cuu/Value?bg. Retrieved 2019-05-20.
- ↑ "Rotational Flattening". http://farside.ph.utexas.edu/teaching/336k/lectures/node109.html.
- ↑ The vector difference r2 − r1 points from object 1 to object 2. See Fig. 11–6. of The Feynman Lectures on Physics, Volume I, equation (9.19) of The Feynman Lectures on Physics, Volume I and Euclidean vector
- ↑ Misner, Charles W. (1973). Gravitation. New York: W. H.Freeman and Company. ISBN 978-0-7167-0344-0. Page 1049.
- ↑ Max Born (1924), Einstein's Theory of Relativity (The 1962 Dover edition, page 348 lists a table documenting the observed and calculated values for the precession of the perihelion of Mercury, Venus, and the Earth.)
- ↑ Greene, Geoffrey L.; Gudkov, Vladimir (2007). "Neutron interferometric method to provide improved constraints on non-Newtonian gravity at the nanometer scale". Physical Review C 75 (1): 015501. doi:10.1103/PhysRevC.75.015501. Bibcode: 2007PhRvC..75a5501G.
- ↑ Leimanis and Minorsky: Our interest is with Leimanis, who first discusses some history about the n-body problem, especially Ms. Kovalevskaya's ~1868–1888, twenty-year complex-variables approach, failure; Section 1: The Dynamics of Rigid Bodies and Mathematical Exterior Ballistics (Chapter 1, the motion of a rigid body about a fixed point (Euler and Poisson equations); Chapter 2, Mathematical Exterior Ballistics), good precursor background to the n-body problem; Section 2: Celestial Mechanics (Chapter 1, The Uniformization of the Three-body Problem (Restricted Three-body Problem); Chapter 2, Capture in the Three-Body Problem; Chapter 3, Generalized n-body Problem).
- ↑ See References sited for Heggie and Hut. This Wikipedia page has made their approach obsolete.
- ↑ Quasi-steady loads refers to the instantaneous inertial loads generated by instantaneous angular velocities and accelerations, as well as translational accelerations (9 variables). It is as though one took a photograph, which also recorded the instantaneous position and properties of motion. In contrast, a steady-state condition refers to a system's state being invariant to time; otherwise, the first derivatives and all higher derivatives are zero.
- ↑ R. M. Rosenberg states the n-body problem similarly (see References): Each particle in a system of a finite number of particles is subjected to a Newtonian gravitational attraction from all the other particles, and to no other forces. If the initial state of the system is given, how will the particles move? Rosenberg failed to realize, like everyone else, that it is necessary to determine the forces first before the motions can be determined.
- ↑ A general, classical solution in terms of first integrals is known to be impossible. An exact theoretical solution for arbitrary n can be approximated via Taylor series, but in practice such an infinite series must be truncated, giving at best only an approximate solution; and an approach now obsolete. In addition, the n-body problem may be solved using numerical integration, but these, too, are approximate solutions; and again obsolete. See Sverre J. Aarseth's book Gravitational N-body Simulations listed in the References.
External links
 |

