Physics:Quadrupole ion trap

Short description: Type of apparatus for isolating charged particles

Scheme of a quadrupole ion trap of classical setup with a particle of positive charge (dark red), surrounded by a cloud of similarly charged particles (light red). The electric field E (blue) is generated by a quadrupole of endcaps (a, positive) and a ring electrode (b). Picture 1 and 2 show two states during an AC cycle.

In experimental physics, a quadrupole ion trap or paul trap is a type of ion trap that uses dynamic electric fields to trap charged particles. They are also called radio frequency (RF) traps or Paul traps in honor of Wolfgang Paul, who invented the device and shared the Nobel Prize in Physics in 1989 for this work. It is used as a component of a mass spectrometer or a trapped ion quantum computer.

Overview

Charged flour grains caught in a quadrupole ion trap

A charged particle, such as an atomic or molecular ion, feels a force from an electric field. It is not possible to create a static configuration of electric fields that traps the charged particle in all three directions (this restriction is known as Earnshaw's theorem). It is possible, however, to create an average confining force in all three directions by use of electric fields that change in time. To do so, the confining and anti-confining directions are switched at a rate faster than it takes the particle to escape the trap. The traps are also called "radio frequency" traps because the switching rate is often at a radio frequency.

The quadrupole is the simplest electric field geometry used in such traps, though more complicated geometries are possible for specialized devices. The electric fields are generated from electric potentials on metal electrodes. A pure quadrupole is created from hyperbolic electrodes, though cylindrical electrodes are often used for ease of fabrication. Microfabricated ion traps exist where the electrodes lie in a plane with the trapping region above the plane. There are two main classes of traps, depending on whether the oscillating field provides confinement in three or two dimensions. In the two-dimension case (a so-called "linear RF trap"), confinement in the third direction is provided by static electric fields.

Theory

thumb| The 3D trap itself generally consists of two hyperbolic metal electrodes with their foci facing each other and a hyperbolic ring electrode halfway between the other two electrodes. The ions are trapped in the space between these three electrodes by AC (oscillating) and DC (static) electric fields. The AC radio frequency voltage oscillates between the two hyperbolic metal end cap electrodes if ion excitation is desired; the driving AC voltage is applied to the ring electrode. The ions are first pulled up and down axially while being pushed in radially. The ions are then pulled out radially and pushed in axially (from the top and bottom). In this way the ions move in a complex motion that generally involves the cloud of ions being long and narrow and then short and wide, back and forth, oscillating between the two states. Since the mid-1980s most 3D traps (Paul traps) have used ~1 mTorr of helium. The use of damping gas and the mass-selective instability mode developed by Stafford et al. led to the first commercial 3D ion traps.

Linear Ion Trap at the University of Calgary

The quadrupole ion trap has two main configurations: the three-dimensional form described above and the linear form made of 4 parallel electrodes. A simplified rectilinear configuration is also used. The advantage of the linear design is its greater storage capacity (in particular of Doppler-cooled ions) and its simplicity, but this leaves a particular constraint on its modeling. The Paul trap is designed to create a saddle-shaped field to trap a charged ion, but with a quadrupole, this saddle-shaped electric field cannot be rotated about an ion in the centre. It can only 'flap' the field up and down. For this reason, the motions of a single ion in the trap are described by Mathieu equations, which can only be solved numerically by computer simulations.

The intuitive explanation and lowest order approximation is the same as strong focusing in accelerator physics. Since the field affects the acceleration, the position lags behind (to lowest order by half a period). So the particles are at defocused positions when the field is focusing and vice versa. Being farther from center, they experience a stronger field when the field is focusing than when it is defocusing.

Equations of motion

Ions in a quadrupole field experience restoring forces that drive them back toward the center of the trap. The motion of the ions in the field is described by solutions to the Mathieu equation. When written for ion motion in a trap, the equation is

[math]\displaystyle{ \frac{d^2u}{d\xi^2}+[a_u-2q_u\cos (2\xi) ]u = 0 }[/math]

(1)

where [math]\displaystyle{ u }[/math] represents the x, y and z coordinates, [math]\displaystyle{ \xi }[/math] is a dimensionless variable given by [math]\displaystyle{ \xi = \Omega t / 2 }[/math], and [math]\displaystyle{ a_u\, }[/math] and [math]\displaystyle{ q_u }[/math] are dimensionless trapping parameters. The parameter [math]\displaystyle{ \Omega }[/math] is the radial frequency of the potential applied to the ring electrode. By using the chain rule, it can be shown that

[math]\displaystyle{ \frac{d^2u}{dt^2} = \frac{\Omega^2}{4} \frac{d^2u}{d\xi^2} }[/math]

(2)

Substituting Equation 2 into the Mathieu Equation 1 yields

[math]\displaystyle{ \frac{4}{\Omega^2}\frac{d^2u}{dt^2} + \left[a_u - 2q_u\cos (\Omega t) \right]u = 0 . }[/math]

(3)

Multiplying by m and rearranging terms shows us that

[math]\displaystyle{ m \frac{d^2u}{dt^2} + m \frac{\Omega^2}{4}\left[a_u - 2q_u\cos (\Omega t) \right]u = 0 . }[/math]

(4)

By Newton's laws of motion, the above equation represents the force on the ion. This equation can be exactly solved using the Floquet theorem or the standard techniques of multiple scale analysis. The particle dynamics and time averaged density of charged particles in a Paul trap can also be obtained by the concept of ponderomotive force.

The forces in each dimension are not coupled, thus the force acting on an ion in, for example, the x dimension is

[math]\displaystyle{ F_x = ma = m\frac{d^2x}{dt^2} = -e \frac{\partial \phi}{\partial x} }[/math]

(5)

Here, [math]\displaystyle{ \phi }[/math] is the quadrupolar potential, given by

[math]\displaystyle{ \phi = \frac{\phi_0}{r_0^2} \bigl( \lambda x^2 + \sigma y^2 + \gamma z^2 \bigr) }[/math]

(6)

where [math]\displaystyle{ \phi _0 }[/math] is the applied electric potential and [math]\displaystyle{ \lambda }[/math], [math]\displaystyle{ \sigma }[/math], and [math]\displaystyle{ \gamma }[/math] are weighting factors, and [math]\displaystyle{ r_0 }[/math] is a size parameter constant. In order to satisfy Laplace's equation, [math]\displaystyle{ \nabla^2\phi_0 = 0 }[/math], it can be shown that

[math]\displaystyle{ \lambda + \sigma + \gamma = 0 \, . }[/math]

For an ion trap, [math]\displaystyle{ \lambda = \sigma = 1 }[/math] and [math]\displaystyle{ \gamma = -2 }[/math] and for a quadrupole mass filter, [math]\displaystyle{ \lambda = -\sigma = 1 }[/math] and [math]\displaystyle{ \gamma = 0 }[/math].

Transforming Equation 6 into a cylindrical coordinate system with [math]\displaystyle{ x = r \cos\theta }[/math], [math]\displaystyle{ y = r \sin\theta }[/math], and [math]\displaystyle{ z = z }[/math] and applying the Pythagorean trigonometric identity [math]\displaystyle{ \sin^2 \theta + \cos^2 \theta = 1 }[/math] gives

Diagram of the stability regions of a quadrupole ion trap according to the voltage and frequency applied to the ion trap elements.

[math]\displaystyle{ \phi_{r,z} = \frac{\phi_0}{r_0^2} \big( r^2 - 2z^2 \big) . }[/math]

(7)

The applied electric potential is a combination of RF and DC given by

[math]\displaystyle{ \phi_0 = U + V\cos \Omega t . }[/math]

(8)

where [math]\displaystyle{ \Omega = 2\pi \nu }[/math] and [math]\displaystyle{ \nu }[/math] is the applied frequency in hertz.

Substituting Equation 8 into Equation 6 with [math]\displaystyle{ \lambda = 1 }[/math] gives

[math]\displaystyle{ \frac{\partial \phi}{\partial x} = \frac {2x}{r_0^2} \big( U + V\cos \Omega t \big) . }[/math]

(9)

Substituting Equation 9 into Equation 5 leads to

[math]\displaystyle{ m\frac {d^2x}{dt^2} = - \frac {2e}{r_0^2} \big( U + V\cos \Omega t \big) x . }[/math]

(10)

Comparing terms on the right hand side of Equation 1 and Equation 10 leads to

[math]\displaystyle{ a_x = \frac {8eU} {m r_0^2 \Omega^2} }[/math]

(11)

and

[math]\displaystyle{ q_x = - \frac {4eV} {m r_0^2 \Omega^2} . }[/math]

(12)

Further [math]\displaystyle{ q_x = q_y\, }[/math],

[math]\displaystyle{ a_z = -\frac {16eU} {m r_0^2 \Omega^2} }[/math]

(13)

and

[math]\displaystyle{ q_z = \frac {8eV} {m r_0^2 \Omega^2} . }[/math]

(14)

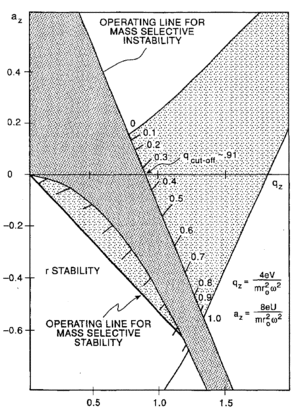
The trapping of ions can be understood in terms of stability regions in [math]\displaystyle{ q_u }[/math] and [math]\displaystyle{ a_u }[/math] space. The boundaries of the shaded regions in the figure are the boundaries of stability in the two directions (also known as boundaries of bands). The domain of overlap of the two regions is the trapping domain. For calculation of these boundaries and similar diagrams as above see Müller-Kirsten.

Linear ion trap

Classical motion of a trapped ion in a radiofrequency (rf) quadrupole (Paul) trap. A quadrupole electric field is displayed for reference. The blue line represents the ion path in the transversal (or radial) direction of a linear trap. The orange line is the secular motion. A linear or a circular secular motion can be generated depending on the initial conditions. Micromotion is the fast oscillation around the secular motion, which is enhanced when a stray dc electric field pushes the ion away from the center of the trap, located at the intersection of the axes. Note how the micromotion is always along the direction of the local rf field

LTQ (Linear trap quadrupole)

The linear ion trap uses a set of quadrupole rods to confine ions radially and a static electrical potential on-end electrodes to confine the ions axially. The linear form of the trap can be used as a selective mass filter, or as an actual trap by creating a potential well for the ions along the axis of the electrodes. Advantages of the linear trap design are increased ion storage capacity, faster scan times, and simplicity of construction (although quadrupole rod alignment is critical, adding a quality control constraint to their production. This constraint is additionally present in the machining requirements of the 3D trap).

Cylindrical ion trap

Ion traps with a cylindrical rather than a hyperbolic ring electrode have been developed and microfabricated in arrays to develop miniature mass spectrometers for chemical detection in medical diagnosis and other fields.

Planar ion trap

Quadrupole traps can also be "unfolded" to create the same effect using a set of planar electrodes. This trap geometry can be made using standard micro-fabrication techniques, including the top metal layer in a standard CMOS microelectronics process, and is a key technology for scaling trapped ion quantum computers to useful numbers of qubits.

Combined radio frequency trap

A combined radio frequency trap is a combination of a Paul ion trap and a Penning trap. One of the main bottlenecks of a quadrupole ion trap is that it can confine only single-charged species or multiple species with similar masses. But in certain applications like antihydrogen production it is important to confine two species of charged particles of widely varying masses. To achieve this objective, a uniform magnetic field is added in the axial direction of the quadrupole ion trap.

Digital ion trap

The digital ion trap (DIT) is a quadrupole ion trap (linear or 3D) that differs from conventional traps by the driving waveform. A DIT is driven by digital signals, typically rectangular waveforms that are generated by switching rapidly between discrete voltage levels. Major advantages of the DIT are its versatility and virtually unlimited mass range. The digital ion trap has been developed mainly as a mass analyzer.

See also

• Quadrupole magnet

Bibliography

• W. Paul Electromagnetic Traps for Charged and Neutral Particles Taken from Proceedings of the International School of Physics <<Enrico Fermi>> Course CXVIII “Laser Manipulation of Atoms and Ions”, (North Holland, New York, 1992) p. 497-517
• R.I. Thompson, T.J. Harmon, and M.G. Ball, The rotating-saddle trap: a mechanical analogy to RF-electric-quadrupole ion trapping? (Canadian Journal of Physics, 2002: 80 12) p. 1433–1448
• M. Welling, H.A. Schuessler, R.I. Thompson, H. Walther Ion/Molecule Reactions, Mass Spectrometry and Optical Spectroscopy in a Linear Ion Trap (International Journal of Mass Spectrometry and Ion Processes, 1998: 172) p. 95-114.
• G. Werth (2005). Charged Particle Traps: Physics and Techniques of Charged Particle Field Confinement (Springer Series on Atomic, Optical, and Plasma Physics). Berlin: Springer. ISBN 3-540-22043-7. OCLC 231588573. 
• John Gillaspy (2001). Trapping Highly Charged Ions: Fundamentals and Applications. Commack, N.Y: Nova Science Publishers. ISBN 1-56072-725-X. OCLC 42009394. 
• Todd, John F. J.; March, Raymond E. (2005). Quadrupole Ion Trap Mass Spectrometry , 2nd Edition. New York: Wiley-Interscience. ISBN 0-471-48888-7. OCLC 56413336. 
• Todd, John F. J.; March, Raymond E. (1995). Practical aspects of ion trap mass spectrometry - Volume I: Fundamentals of Ion Trap Mass Spectrometry. Boca Raton: CRC Press. ISBN 0-8493-4452-2. OCLC 32346425. 
• Todd, John F. J.; March, Raymond E. (1995). Practical aspects of ion trap mass spectrometry: Ion Trap Instrumentation, Vol. 2. Boca Raton: CRC Press. ISBN 0-8493-8253-X. OCLC 32346425. 
• Todd, John F. J.; March, Raymond E. (1995). Practical aspects of ion trap mass spectrometry, Vol. 3. Boca Raton: CRC Press. ISBN 0-8493-8251-3. OCLC 32346425. 
• Hughes, Richard M.; March, Raymond E.; Todd, John F. J. (1989). Quadrupole storage mass spectrometry. New York: Wiley. ISBN 0-471-85794-7. OCLC 18290778. 
• K. Shah and H. Ramachandran, Analytic, nonlinearly exact solutions for an rf confined plasma, Phys. Plasmas 15, 062303 (2008), [1]
• Pradip K. Ghosh, Ion Traps, International Series of Monographs in Physics, Oxford University Press (1995), https://web.archive.org/web/20111102190045/http://www.oup.com/us/catalog/general/subject/Physics/AtomicMolecularOpticalphysics/?view=usa

Patents

• DE patent 944900 "Verfahren zur Trennung bzw. zum getrennten Nachweis von Ionen verschiedener spezifischer Ladung", W. Paul and H. Steinwedel, filed on December 24, 1953
• GB patent 773689 "Improved arrangements for separating or separately detecting charged particles of different specific charges", W. Paul, claims priority of the above German application filed on December 24, 1953
• US patent 2939952 "Apparatus for separating charged particles of different specific charges", W. Paul and H. Steinwedel, claims priority of the above German application filed on December 24, 1953

External links

• Nobel Prize in Physics 1989