Physics:Mass (mass spectrometry)
The mass recorded by a mass spectrometer can refer to different physical quantities depending on the characteristics of the instrument and the manner in which the mass spectrum is displayed.
Units
The dalton (symbol: Da) is the standard unit that is used for indicating mass on an atomic or molecular scale (atomic mass).[1] The unified atomic mass unit (symbol: u) is equivalent to the dalton. One dalton is approximately the mass of one a single proton or neutron.[2] The unified atomic mass unit has a value of 1.660538921(73)×10−27 kg.[3] The amu without the "unified" prefix is an obsolete unit based on oxygen, which was replaced in 1961.
Molecular mass

The molecular mass (abbreviated Mr) of a substance, formerly also called molecular weight and abbreviated as MW, is the mass of one molecule of that substance, relative to the unified atomic mass unit u (equal to 1/12 the mass of one atom of 12C). Due to this relativity, the molecular mass of a substance is commonly referred to as the relative molecular mass, and abbreviated to Mr.
Average mass
The average mass of a molecule is obtained by summing the average atomic masses of the constituent elements. For example, the average mass of natural water with formula H2O is 1.00794 + 1.00794 + 15.9994 = 18.01528 Da.
Mass number
The mass number, also called the nucleon number, is the number of protons and neutrons in an atomic nucleus. The mass number is unique for each isotope of an element and is written either after the element name or as a superscript to the left of an element's symbol. For example, carbon-12 (12C) has 6 protons and 6 neutrons.
Nominal mass
The nominal mass for an element is the mass number of its most abundant naturally occurring stable isotope, and for an ion or molecule, the nominal mass is the sum of the nominal masses of the constituent atoms.[4][5] Isotope abundances are tabulated by IUPAC:[6] for example carbon has two stable isotopes 12C at 98.9% natural abundance and 13C at 1.1% natural abundance, thus the nominal mass of carbon is 12. The nominal mass is not always the lowest mass number, for example iron has isotopes 54Fe, 56Fe, 57Fe, and 58Fe with abundances 6%, 92%, 2%, and 0.3%, respectively, and a nominal mass of 56 Da. For a molecule, the nominal mass is obtained by summing the nominal masses of the constituent elements, for example water has two hydrogen atoms with nominal mass 1 Da and one oxygen atom with nominal mass 16 Da, therefore the nominal mass of H2O is 18 Da.
In mass spectrometry, the difference between the nominal mass and the monoisotopic mass is the mass defect.[7] This differs from the definition of mass defect used in physics which is the difference between the mass of a composite particle and the sum of the masses of its constituent parts.[8]
Accurate mass
The accurate mass (more appropriately, the measured accurate mass[9]) is an experimentally determined mass that allows the elemental composition to be determined.[10] For molecules with mass below 200 Da, 5 ppm accuracy is often sufficient to uniquely determine the elemental composition.[11]
Exact mass
The exact mass of an isotopic species (more appropriately, the calculated exact mass[9]) is obtained by summing the masses of the individual isotopes of the molecule. For example, the exact mass of water containing two hydrogen-1 (1H) and one oxygen-16 (16O) is 1.0078 + 1.0078 + 15.9949 = 18.0105 Da. The exact mass of heavy water, containing two hydrogen-2 (deuterium or 2H) and one oxygen-16 (16O) is 2.0141 + 2.0141 + 15.9949 = 20.0229 Da.
When an exact mass value is given without specifying an isotopic species, it normally refers to the most abundant isotopic species.
Monoisotopic mass
The monoisotopic mass is the sum of the masses of the atoms in a molecule using the unbound, ground-state, rest mass of the principal (most abundant) isotope for each element.[12][5] The monoisotopic mass of a molecule or ion is the exact mass obtained using the principal isotopes. Monoisotopic mass is typically expressed in daltons.
For typical organic compounds, where the monoisotopic mass is most commonly used, this also results in the lightest isotope being selected. For some heavier atoms such as iron and argon the principal isotope is not the lightest isotope. The mass spectrum peak corresponding to the monoisotopic mass is often not observed for large molecules, but can be determined from the isotopic distribution.[13]
Most abundant mass
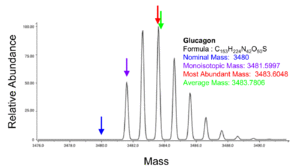
This refers to the mass of the molecule with the most highly represented isotope distribution, based on the natural abundance of the isotopes.[14]
Isotopomer and isotopologue
Isotopomers (isotopic isomers) are isomers having the same number of each isotopic atom, but differing in the positions of the isotopic atoms.[15] For example, CH3CHDCH3 and CH3CH2CH2D are a pair of structural isotopomers.
Isotopomers should not be confused with isotopologues, which are chemical species that differ in the isotopic composition of their molecules or ions. For example, three isotopologues of the water molecule with different isotopic composition of hydrogen are: HOH, HOD and DOD, where D stands for deuterium (2H).
Kendrick mass
The Kendrick mass is a mass obtained by multiplying the measured mass by a numeric factor. The Kendrick mass is used to aid in the identification of molecules of similar chemical structure from peaks in mass spectra.[16][17] The method of stating mass was suggested in 1963 by the chemist Edward Kendrick.
According to the procedure outlined by Kendrick, the mass of CH2 is defined as 14.000 Da, instead of 14.01565 Da.[18][19]
The Kendrick mass for a family of compounds is given by[20]
For hydrocarbon analysis, = CH2.
Mass defect (mass spectrometry)
The mass defect used in nuclear physics is different from its use in mass spectrometry. In nuclear physics, the mass defect is the difference in the mass of a composite particle and the sum of the masses of its component parts. In mass spectrometry the mass defect is defined as the difference between the exact mass and the nearest integer mass.[21][22]
The Kendrick mass defect is the exact Kendrick mass subtracted from the nearest integer Kendrick mass.[23]
Mass defect filtering can be used to selectively detect compounds with a mass spectrometer based on their chemical composition.[7]
Packing fraction (mass spectrometry)

The term packing fraction was defined by Aston as the difference of the measured mass M and the nearest integer mass I (based on the oxygen-16 mass scale) divided by the quantity comprising the mass number multiplied by ten thousand:[26]
- .
Aston's early model of nuclear structure (prior to the discovery of the neutron) postulated that the electromagnetic fields of closely packed protons and electrons in the nucleus would interfere and a fraction of the mass would be destroyed.[27] A low packing fraction is indicative of a stable nucleus.[28]
Nitrogen rule
The nitrogen rule states that organic compounds containing exclusively hydrogen, carbon, nitrogen, oxygen, silicon, phosphorus, sulfur, and the halogens either have an odd nominal mass that indicates an odd number of nitrogen atoms are present or an even nominal mass that indicates an even number of nitrogen atoms are present in the molecular ion.[29][30]
Prout's hypothesis and the whole number rule
The whole number rule states that the masses of the isotopes are integer multiples of the mass of the hydrogen atom.[31] The rule is a modified version of Prout's hypothesis proposed in 1815, to the effect that atomic weights are multiples of the weight of the hydrogen atom.[32]
See also
- List of elements by atomic mass
- Dalton (unit)
References
- ↑ Bureau International des Poids et Mesures (2019): The International System of Units (SI), 9th edition, English version, page 134. Available at the BIPM website.
- ↑ Stryer, Jeremy M. Berg; John L. Tymoczko; Lubert (2007). "2". Biochemistry (3rd print, 6th ed.). New York: Freeman. p. 35. ISBN 978-0-7167-8724-2.
- ↑ Fundamental Physical Constants from NIST
- ↑ Jürgen H Gross (14 February 2011). Mass Spectrometry: A Textbook. Springer Science & Business Media. pp. 71–. ISBN 978-3-642-10709-2. https://books.google.com/books?id=xHOQiaquq24C&pg=PA71.
- ↑ 5.0 5.1 J. Throck Watson; O. David Sparkman (9 July 2013). Introduction to Mass Spectrometry: Instrumentation, Applications, and Strategies for Data Interpretation. John Wiley & Sons. pp. 385–. ISBN 978-1-118-68158-9. https://books.google.com/books?id=mUsSAAAAQBAJ&pg=PT385.
- ↑ Berglund, Michael; Wieser, Michael E. (2011). "Isotopic compositions of the elements 2009 (IUPAC Technical Report)". Pure and Applied Chemistry 83 (2): 397–410. doi:10.1351/PAC-REP-10-06-02. ISSN 1365-3075.
- ↑ 7.0 7.1 Sleno, Lekha (2012). "The use of mass defect in modern mass spectrometry". Journal of Mass Spectrometry 47 (2): 226–236. doi:10.1002/jms.2953. ISSN 1076-5174. PMID 22359333. Bibcode: 2012JMSp...47..226S.
- ↑ Imma Ferrer; E. M. Thurman (6 May 2009). Liquid Chromatography Time-of-Flight Mass Spectrometry. John Wiley & Sons. pp. 18–22. ISBN 978-0-470-42995-2. https://books.google.com/books?id=nhU0dZ9sklwC&pg=PA19.
- ↑ 9.0 9.1 O. David Sparkman (2006). Mass Spec Desk Reference (2nd. ed.). p. 60. ISBN 0-9660813-9-0.
- ↑ Grange AH; Winnik W; Ferguson PL; Sovocool GW (2005), "Using a triple-quadrupole mass spectrometer in accurate mass mode and an ion correlation program to identify compounds", Rapid Commun. Mass Spectrom. 19 (18): 2699–715, doi:10.1002/rcm.2112, PMID 16124033, Bibcode: 2005RCMS...19.2699G, https://zenodo.org/record/1229344.
- ↑ Gross, M. L. (1994), "Accurate Masses for Structure Confirmation", J. Am. Soc. Mass Spectrom. 5 (2): 57, doi:10.1016/1044-0305(94)85036-4, PMID 24222515.
- ↑ "Monoisotopic mass spectrum". 2009. doi:10.1351/goldbook.M04014. ISBN 978-0-9678550-9-7.
- ↑ Senko, Michael W.; Beu, Steven C.; McLaffertycor, Fred W. (1995). "Determination of monoisotopic masses and ion populations for large biomolecules from resolved isotopic distributions". Journal of the American Society for Mass Spectrometry 6 (4): 229–233. doi:10.1016/1044-0305(95)00017-8. ISSN 1044-0305. PMID 24214167.
- ↑ Goraczko AJ (2005), "Molecular mass and location of the most abundant peak of the molecular ion isotopomeric cluster", Journal of Molecular Modeling 11 (4–5): 271–7, doi:10.1007/s00894-005-0245-x, PMID 15928922.
- ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "isotopomer". doi:10.1351/goldbook.I03352
- ↑ Kendrick, Edward (1963), "A mass scale based on CH2 = 14.0000 for high resolution mass spectrometry of organic compounds", Anal. Chem. 35 (13): 2146–2154, doi:10.1021/ac60206a048.
- ↑ Marshall AG; Rodgers RP (January 2004), "Petroleomics: the next grand challenge for chemical analysis", Acc. Chem. Res. 37 (1): 53–9, doi:10.1021/ar020177t, PMID 14730994.
- ↑ Mopper, Kenneth; Stubbins, Aron; Ritchie, Jason D.; Bialk, Heidi M.; Hatcher, Patrick G. (2007), "Advanced Instrumental Approaches for Characterization of Marine Dissolved Organic Matter: Extraction Techniques, Mass Spectrometry, and Nuclear Magnetic Resonance Spectroscopy", Chemical Reviews 107 (2): 419–42, doi:10.1021/cr050359b, PMID 17300139
- ↑ Meija, Juris (2006), "Mathematical tools in analytical mass spectrometry", Analytical and Bioanalytical Chemistry 385 (3): 486–99, doi:10.1007/s00216-006-0298-4, PMID 16514517
- ↑ Kim, Sunghwan; Kramer, Robert W.; Hatcher, Patrick G. (2003), "Graphical Method for Analysis of Ultrahigh-Resolution Broadband Mass Spectra of Natural Organic Matter, the Van Krevelen Diagram", Analytical Chemistry 75 (20): 5336–44, doi:10.1021/ac034415p, PMID 14710810
- ↑ J. Throck Watson; O. David Sparkman (4 December 2007). Introduction to Mass Spectrometry: Instrumentation, Applications, and Strategies for Data Interpretation. John Wiley & Sons. pp. 274–. ISBN 978-0-470-51634-8. https://books.google.com/books?id=ox1bWqYqZT4C&pg=PA274.
- ↑ Jürgen H Gross (22 June 2017). Mass Spectrometry: A Textbook. Springer. pp. 143–. ISBN 978-3-319-54398-7. https://books.google.com/books?id=PdMnDwAAQBAJ&pg=PA143.
- ↑ Hughey, Christine A.; Hendrickson, Christopher L.; Rodgers, Ryan P.; Marshall, Alan G.; Qian, Kuangnan (2001). "Kendrick Mass Defect Spectrum: A Compact Visual Analysis for Ultrahigh-Resolution Broadband Mass Spectra". Analytical Chemistry 73 (19): 4676–4681. doi:10.1021/ac010560w. ISSN 0003-2700. PMID 11605846.
- ↑ "The Nobel Prize in Chemistry 1922". Nobel Foundation. http://nobelprize.org/nobel_prizes/chemistry/laureates/1922/.
- ↑ Squires, Gordon (1998). "Francis Aston and the mass spectrograph". Dalton Transactions (23): 3893–3900. doi:10.1039/a804629h.
- ↑ Aston, F. W. (1927). "Atoms and their Packing Fractions1". Nature 120 (3035): 956–959. doi:10.1038/120956a0. ISSN 0028-0836. Bibcode: 1927Natur.120..956A.
- ↑ Budzikiewicz, Herbert; Grigsby, Ronald D. (2006). "Mass spectrometry and isotopes: A century of research and discussion". Mass Spectrometry Reviews 25 (1): 146–157. doi:10.1002/mas.20061. ISSN 0277-7037. PMID 16134128. Bibcode: 2006MSRv...25..146B.
- ↑ Dempster, A. J. (1938). "The Energy Content of the Heavy Nuclei". Physical Review 53 (11): 869–874. doi:10.1103/PhysRev.53.869. ISSN 0031-899X. Bibcode: 1938PhRv...53..869D.
- ↑ Tureček, František; McLafferty, Fred W. (1993). Interpretation of mass spectra. Sausalito, Calif: University Science Books. pp. 37–38. ISBN 978-0-935702-25-5.
- ↑ David O. Sparkman (2007). Mass Spectrometry Desk Reference. Pittsburgh: Global View Pub. p. 64. ISBN 978-0-9660813-9-8.
- ↑ Budzikiewicz H; Grigsby RD (2006). "Mass spectrometry and isotopes: a century of research and discussion". Mass Spectrometry Reviews 25 (1): 146–57. doi:10.1002/mas.20061. PMID 16134128. Bibcode: 2006MSRv...25..146B.
- ↑ Prout, William (1815). "On the relation between the specific gravities of bodies in their gaseous state and the weights of their atoms.". Annals of Philosophy 6: 321–330. http://web.lemoyne.edu/~giunta/PROUT.HTML. Retrieved 2007-09-08.
External links
 |

