Physics:SAMV (algorithm)
SAMV (iterative sparse asymptotic minimum variance[1][2]) is a parameter-free superresolution algorithm for the linear inverse problem in spectral estimation, direction-of-arrival (DOA) estimation and tomographic reconstruction with applications in signal processing, medical imaging and remote sensing. The name was coined in 2013[1] to emphasize its basis on the asymptotically minimum variance (AMV) criterion. It is a powerful tool for the recovery of both the amplitude and frequency characteristics of multiple highly correlated sources in challenging environments (e.g., limited number of snapshots and low signal-to-noise ratio). Applications include synthetic-aperture radar,[2][3] computed tomography scan, and magnetic resonance imaging (MRI).
Definition
The formulation of the SAMV algorithm is given as an inverse problem in the context of DOA estimation. Suppose an [math]\displaystyle{ M }[/math]-element uniform linear array (ULA) receive [math]\displaystyle{ K }[/math] narrow band signals emitted from sources located at locations [math]\displaystyle{ \mathbf{\theta} = \{\theta_a, \ldots, \theta_K \} }[/math], respectively. The sensors in the ULA accumulates [math]\displaystyle{ N }[/math] snapshots over a specific time. The [math]\displaystyle{ M \times 1 }[/math] dimensional snapshot vectors are
- [math]\displaystyle{ \mathbf{y}(n) = \mathbf{A} \mathbf{x}(n) + \mathbf{e}(n), n = 1, \ldots, N }[/math]
where [math]\displaystyle{ \mathbf{A} = [ \mathbf{a}(\theta_1), \ldots, \mathbf{a}(\theta_K) ] }[/math] is the steering matrix, [math]\displaystyle{ {\bf x}(n)=[{\bf x}_1(n), \ldots, {\bf x}_K(n)]^T }[/math] contains the source waveforms, and [math]\displaystyle{ {\bf e}(n) }[/math] is the noise term. Assume that [math]\displaystyle{ \mathbf{E}\left({\bf e}(n){\bf e}^H(\bar{n})\right)= \sigma{\bf I}_M\delta_{n,\bar{n}} }[/math], where [math]\displaystyle{ \delta_{n,\bar{n}} }[/math] is the Dirac delta and it equals to 1 only if [math]\displaystyle{ n=\bar{n} }[/math] and 0 otherwise. Also assume that [math]\displaystyle{ {\bf e}(n) }[/math] and [math]\displaystyle{ {\bf x}(n) }[/math] are independent, and that [math]\displaystyle{ \mathbf{E}\left({\bf x}(n){\bf x}^H(\bar{n})\right)={\bf P}\delta_{n,\bar{n}} }[/math], where [math]\displaystyle{ {\bf P}= \operatorname{Diag}( {p_1,\ldots,p_K}) }[/math]. Let [math]\displaystyle{ {\bf p} }[/math] be a vector containing the unknown signal powers and noise variance, [math]\displaystyle{ {\bf p} = [p_1,\ldots,p_K, \sigma]^T }[/math].
The covariance matrix of [math]\displaystyle{ {\bf y}(n) }[/math] that contains all information about [math]\displaystyle{ \boldsymbol{\bf p} }[/math] is
- [math]\displaystyle{ {\bf R} = {\bf A}{\bf P}{\bf A}^H+\sigma{\bf I}. }[/math]
This covariance matrix can be traditionally estimated by the sample covariance matrix [math]\displaystyle{ {\bf R}_{N} = {\bf Y}{\bf Y}^H/N }[/math] where [math]\displaystyle{ {\bf Y} =[{\bf y}(1), \ldots,{\bf y}(N)] }[/math]. After applying the vectorization operator to the matrix [math]\displaystyle{ {\bf R} }[/math], the obtained vector [math]\displaystyle{ {\bf r}(\boldsymbol{\bf p}) = \operatorname{vec}({\bf R}) }[/math] is linearly related to the unknown parameter [math]\displaystyle{ \boldsymbol{\bf p} }[/math] as
[math]\displaystyle{ {\bf r}(\boldsymbol{\bf p}) = \operatorname{vec}({\bf R})={\bf S}\boldsymbol{\bf p} }[/math],
where [math]\displaystyle{ {\bf S}= [{\bf S}_1,\bar{\bf a}_{K+1}] }[/math], [math]\displaystyle{ {\bf S}_1 =[\bar{\bf a}_1,\ldots,\bar{\bf a}_K] }[/math], [math]\displaystyle{ \bar{\bf a}_k = {\bf a}^{*}_k \otimes{\bf a}_k }[/math], [math]\displaystyle{ k=1,\ldots, K }[/math], and let [math]\displaystyle{ \bar{\bf a}_{K+1} = \operatorname{vec}({\bf I}) }[/math] where [math]\displaystyle{ \otimes }[/math] is the Kronecker product.
SAMV algorithm
To estimate the parameter [math]\displaystyle{ \boldsymbol{\bf p} }[/math] from the statistic [math]\displaystyle{ {\bf r}_N }[/math], we develop a series of iterative SAMV approaches based on the asymptotically minimum variance criterion. From,[1] the covariance matrix [math]\displaystyle{ \operatorname{Cov}^\operatorname{Alg}_{\boldsymbol{p}} }[/math] of an arbitrary consistent estimator of [math]\displaystyle{ \boldsymbol{p} }[/math] based on the second-order statistic [math]\displaystyle{ {\bf r}_N }[/math] is bounded by the real symmetric positive definite matrix
- [math]\displaystyle{ \operatorname{Cov}^\operatorname{Alg}_{\boldsymbol{p}}\geq[{\bf S}^H_d {\bf C}^{-1}_r{\bf S}_d]^{-1}, }[/math]
where [math]\displaystyle{ {\bf S}_d = {\rm d}{\bf r}(\boldsymbol{p})/ {\rm d}\boldsymbol{p} }[/math]. In addition, this lower bound is attained by the covariance matrix of the asymptotic distribution of [math]\displaystyle{ \hat{\bf p} }[/math] obtained by minimizing,
- [math]\displaystyle{ \hat{\boldsymbol{p}} =\arg \min_{\boldsymbol{p}} f(\boldsymbol{p}), }[/math]
where [math]\displaystyle{ f(\boldsymbol{p}) = [{\bf r}_N-{\bf r}(\boldsymbol{p})]^H {\bf C}_r^{-1} [{\bf r}_N-{\bf r}(\boldsymbol{p})]. }[/math]
Therefore, the estimate of [math]\displaystyle{ \boldsymbol{\bf p} }[/math] can be obtained iteratively.
The [math]\displaystyle{ \{\hat{p}_k\}_{k=1}^K }[/math] and [math]\displaystyle{ \hat{\sigma} }[/math] that minimize [math]\displaystyle{ f(\boldsymbol{p}) }[/math] can be computed as follows. Assume [math]\displaystyle{ \hat{p}^{(i)}_k }[/math] and [math]\displaystyle{ \hat{\sigma}^{(i)} }[/math] have been approximated to a certain degree in the [math]\displaystyle{ i }[/math]th iteration, they can be refined at the [math]\displaystyle{ (i+1) }[/math]th iteration by,
- [math]\displaystyle{ \hat{p}^{(i+1)}_k = \frac{{\bf a}^H_k{\bf R}^{-1{(i)}}{\bf R}_N {\bf R}^{-1{(i)}}{\bf a}_k}{ ({\bf a}^H_k{\bf R}^{-1{(i)}}{\bf a}_k)^2}+\hat{p}^{(i)}_k-\frac{1}{{\bf a}^H_k{\bf R}^{-1{(i)}}{\bf a}_k}, \quad k=1, \ldots,K }[/math]
- [math]\displaystyle{ \hat{\sigma}^{(i+1)} = \left(\operatorname{Tr}({\bf R}^{-2^{(i)}}{\bf R}_N) + \hat{\sigma}^{(i)}\operatorname{Tr}({\bf R}^{-2^{(i)}}) -\operatorname{Tr}({\bf R}^{-1^{(i)}})\right)/{\operatorname{Tr}{({\bf R}^{-2^{(i)}})}}, }[/math]
where the estimate of [math]\displaystyle{ {\bf R} }[/math] at the [math]\displaystyle{ i }[/math]th iteration is given by [math]\displaystyle{ {\bf R}^{(i)}={\bf A}{\bf P}^{(i)}{\bf A}^H+\hat{\sigma}^{(i)}{\bf I} }[/math] with [math]\displaystyle{ {\bf P}^{(i)}=\operatorname{Diag}(\hat{p}^{(i)}_1, \ldots, \hat{p}^{(i)}_K) }[/math].
Beyond scanning grid accuracy
The resolution of most compressed sensing based source localization techniques is limited by the fineness of the direction grid that covers the location parameter space.[4] In the sparse signal recovery model, the sparsity of the truth signal [math]\displaystyle{ \mathbf{x}(n) }[/math] is dependent on the distance between the adjacent element in the overcomplete dictionary [math]\displaystyle{ {\bf A} }[/math], therefore, the difficulty of choosing the optimum overcomplete dictionary arises. The computational complexity is directly proportional to the fineness of the direction grid, a highly dense grid is not computational practical. To overcome this resolution limitation imposed by the grid, the grid-free SAMV-SML (iterative Sparse Asymptotic Minimum Variance - Stochastic Maximum Likelihood) is proposed,[1] which refine the location estimates [math]\displaystyle{ \boldsymbol{\bf \theta}=(\theta_1,\ldots,\theta_K)^T }[/math] by iteratively minimizing a stochastic maximum likelihood cost function with respect to a single scalar parameter [math]\displaystyle{ \theta_k }[/math].
Application to range-Doppler imaging
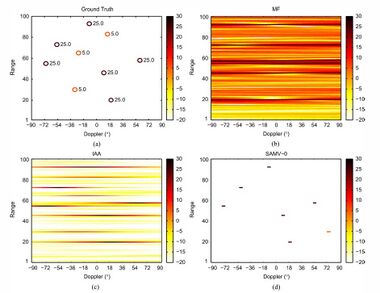
A typical application with the SAMV algorithm in SISO radar/sonar range-Doppler imaging problem. This imaging problem is a single-snapshot application, and algorithms compatible with single-snapshot estimation are included, i.e., matched filter (MF, similar to the periodogram or backprojection, which is often efficiently implemented as fast Fourier transform (FFT)), IAA,[5] and a variant of the SAMV algorithm (SAMV-0). The simulation conditions are identical to:[5] A [math]\displaystyle{ 30 }[/math]-element polyphase pulse compression P3 code is employed as the transmitted pulse, and a total of nine moving targets are simulated. Of all the moving targets, three are of [math]\displaystyle{ 5 }[/math] dB power and the rest six are of [math]\displaystyle{ 25 }[/math] dB power. The received signals are assumed to be contaminated with uniform white Gaussian noise of [math]\displaystyle{ 0 }[/math] dB power.
The matched filter detection result suffers from severe smearing and leakage effects both in the Doppler and range domain, hence it is impossible to distinguish the [math]\displaystyle{ 5 }[/math] dB targets. On contrary, the IAA algorithm offers enhanced imaging results with observable target range estimates and Doppler frequencies. The SAMV-0 approach provides highly sparse result and eliminates the smearing effects completely, but it misses the weak [math]\displaystyle{ 5 }[/math] dB targets.
Open source implementation
An open source MATLAB implementation of SAMV algorithm could be downloaded here.
See also
- Array processing
- Matched filter – Filters used in signal processing that are optimal in some sense.
- Periodogram – Estimate of the spectral density of a signal
- Filtered backprojection – Integral transform (Radon transform)
- MUltiple SIgnal Classification – Algorithm used for frequency estimation and radio direction finding (MUSIC), a popular parametric superresolution method
- Physics:Pulse-Doppler radar – Type of radar system
- Super-resolution imaging – Any technique to improve resolution of an imaging system beyond conventional limits
- Compressed sensing – Signal processing technique
- Inverse problem – Process of calculating the causal factors that produced a set of observations
- Tomographic reconstruction – Estimate object properties from a finite number of projections
References
- ↑ 1.0 1.1 1.2 1.3 1.4 Abeida, Habti; Zhang, Qilin; Li, Jian; Merabtine, Nadjim (2013). "Iterative Sparse Asymptotic Minimum Variance Based Approaches for Array Processing". IEEE Transactions on Signal Processing 61 (4): 933–944. doi:10.1109/tsp.2012.2231676. ISSN 1053-587X. Bibcode: 2013ITSP...61..933A. https://qilin-zhang.github.io/_pages/pdfs/SAMVpaper.pdf.
- ↑ 2.0 2.1 Glentis, George-Othon; Zhao, Kexin; Jakobsson, Andreas; Abeida, Habti; Li, Jian (2014). "SAR imaging via efficient implementations of sparse ML approaches". Signal Processing 95: 15–26. doi:10.1016/j.sigpro.2013.08.003. http://portal.research.lu.se/ws/files/1868394/4076845.pdf.
- ↑ Yang, Xuemin; Li, Guangjun; Zheng, Zhi (2015-02-03). "DOA Estimation of Noncircular Signal Based on Sparse Representation". Wireless Personal Communications 82 (4): 2363–2375. doi:10.1007/s11277-015-2352-z.
- ↑ Malioutov, D.; Cetin, M.; Willsky, A.S. (2005). "A sparse signal reconstruction perspective for source localization with sensor arrays". IEEE Transactions on Signal Processing 53 (8): 3010–3022. doi:10.1109/tsp.2005.850882. Bibcode: 2005ITSP...53.3010M.
- ↑ 5.0 5.1 Yardibi, Tarik; Li, Jian; Stoica, Petre; Xue, Ming; Baggeroer, Arthur B. (2010). "Source Localization and Sensing: A Nonparametric Iterative Adaptive Approach Based on Weighted Least Squares". IEEE Transactions on Aerospace and Electronic Systems 46 (1): 425–443. doi:10.1109/taes.2010.5417172. Bibcode: 2010ITAES..46..425Y.
 |

