Finance:Non-convexity (economics)

From HandWiki
Revision as of 18:39, 5 February 2024 by OrgMain (talk | contribs) (url)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Violations of the convexity assumptions of elementary economics

In economics, non-convexity refers to violations of the convexity assumptions of elementary economics. Basic economics textbooks concentrate on consumers with convex preferences (that do not prefer extremes to in-between values) and convex budget sets and on producers with convex production sets; for convex models, the predicted economic behavior is well understood.[1][2] When convexity assumptions are violated, then many of the good properties of competitive markets need not hold: Thus, non-convexity is associated with market failures,[3][4] where supply and demand differ or where market equilibria can be inefficient.[1][4][5][6][7][8] Non-convex economies are studied with nonsmooth analysis, which is a generalization of convex analysis.[8][9][10][11]

Demand with many consumers

If a preference set is non-convex, then some prices determine a budget-line that supports two separate optimal-baskets. For example, we can imagine that, for zoos, a lion costs as much as an eagle, and further that a zoo's budget suffices for one eagle or one lion. We can suppose also that a zoo-keeper views either animal as equally valuable. In this case, the zoo would purchase either one lion or one eagle. Of course, a contemporary zoo-keeper does not want to purchase half of an eagle and half of a lion. Thus, the zoo-keeper's preferences are non-convex: The zoo-keeper prefers having either animal to having any strictly convex combination of both.

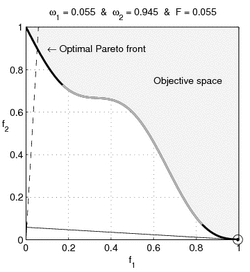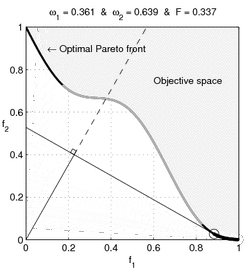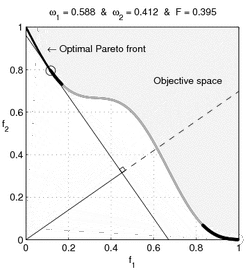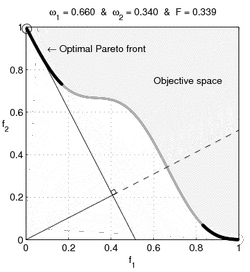
When consumer preferences have concavities, then the linear budgets need not support an equilibrium: Consumers can jump between two separate allocations (of equal utility).

When the consumer's preference set is non-convex, then (for some prices) the consumer's demand is not connected; A disconnected demand implies some discontinuous behavior by the consumer, as discussed by Harold Hotelling:

If indifference curves for purchases be thought of as possessing a wavy character, convex to the origin in some regions and concave in others, we are forced to the conclusion that it is only the portions convex to the origin that can be regarded as possessing any importance, since the others are essentially unobservable. They can be detected only by the discontinuities that may occur in demand with variation in price-ratios, leading to an abrupt jumping of a point of tangency across a chasm when the straight line is rotated. But, while such discontinuities may reveal the existence of chasms, they can never measure their depth. The concave portions of the indifference curves and their many-dimensional generalizations, if they exist, must forever remain in unmeasurable obscurity.[12]

The difficulties of studying non-convex preferences were emphasized by Herman Wold[13] and again by Paul Samuelson, who wrote that non-convexities are "shrouded in eternal darkness ...",[14] according to Diewert.[15]

When convexity assumptions are violated, then many of the good properties of competitive markets need not hold: Thus, non-convexity is associated with market failures, where supply and demand differ or where market equilibria can be inefficient.[1] Non-convex preferences were illuminated from 1959 to 1961 by a sequence of papers in The Journal of Political Economy (JPE). The main contributors were Michael Farrell,[16] Francis Bator,[17] Tjalling Koopmans,[18] and Jerome Rothenberg.[19] In particular, Rothenberg's paper discussed the approximate convexity of sums of non-convex sets.[20] These JPE-papers stimulated a paper by Lloyd Shapley and Martin Shubik, which considered convexified consumer-preferences and introduced the concept of an "approximate equilibrium".[21] The JPE-papers and the Shapley–Shubik paper influenced another notion of "quasi-equilibria", due to Robert Aumann.[22][23]

Non-convex sets have been incorporated in the theories of general economic equilibria.[24] These results are described in graduate-level textbooks in microeconomics,[25] general equilibrium theory,[26] game theory,[27] mathematical economics,[28] and applied mathematics (for economists).[29] The Shapley–Folkman lemma establishes that non-convexities are compatible with approximate equilibria in markets with many consumers; these results also apply to production economies with many small firms.[30]

Supply with few producers

Non-convexity is important under oligopolies and especially monopolies.[8] Concerns with large producers exploiting market power initiated the literature on non-convex sets, when Piero Sraffa wrote about on firms with increasing returns to scale in 1926,[31] after which Harold Hotelling wrote about marginal cost pricing in 1938.[32] Both Sraffa and Hotelling illuminated the market power of producers without competitors, clearly stimulating a literature on the supply-side of the economy.[33]

Contemporary economics

Recent research in economics has recognized non-convexity in new areas of economics. In these areas, non-convexity is associated with market failures, where equilibria need not be efficient or where no competitive equilibrium exists because supply and demand differ.[1][4][5][6][7][8] Non-convex sets arise also with environmental goods (and other externalities),[6][7] and with market failures,[3] and public economics.[5][34] Non-convexities occur also with information economics,[35] and with stock markets[8] (and other incomplete markets).[36][37] Such applications continued to motivate economists to study non-convex sets.[1] In some cases, non-linear pricing or bargaining may overcome the failures of markets with competitive pricing; in other cases, regulation may be justified.

Optimization over time

The previously mentioned applications concern non-convexities in finite-dimensional vector spaces, where points represent commodity bundles. However, economists also consider dynamic problems of optimization over time, using the theories of differential equations, dynamic systems, stochastic processes, and functional analysis: Economists use the following optimization methods:

In these theories, regular problems involve convex functions defined on convex domains, and this convexity allows simplifications of techniques and economic meaningful interpretations of the results.[43][44][45] In economics, dynamic programing was used by Martin Beckmann and Richard F. Muth for work on inventory theory and consumption theory.[46] Robert C. Merton used dynamic programming in his 1973 article on the intertemporal capital asset pricing model.[47] (See also Merton's portfolio problem). In Merton's model, investors chose between income today and future income or capital gains, and their solution is found via dynamic programming. Stokey, Lucas & Prescott use dynamic programming to solve problems in economic theory, problems involving stochastic processes.[48] Dynamic programming has been used in optimal economic growth, resource extraction, principal–agent problems, public finance, business investment, asset pricing, factor supply, and industrial organization. Ljungqvist & Sargent apply dynamic programming to study a variety of theoretical questions in monetary policy, fiscal policy, taxation, economic growth, search theory, and labor economics.[49] Dixit & Pindyck used dynamic programming for capital budgeting.[50] For dynamic problems, non-convexities also are associated with market failures,[51] just as they are for fixed-time problems.[52]

Nonsmooth analysis

Economists have increasingly studied non-convex sets with nonsmooth analysis, which generalizes convex analysis. Convex analysis centers on convex sets and convex functions, for which it provides powerful ideas and clear results, but it is not adequate for the analysis of non-convexities, such as increasing returns to scale.[53] "Non-convexities in [both] production and consumption ... required mathematical tools that went beyond convexity, and further development had to await the invention of non-smooth calculus": For example, Clarke's differential calculus for Lipschitz continuous functions, which uses Rademacher's theorem and which is described by (Rockafellar Wets)[54] and (Mordukhovich 2006),[9] according to (Khan 2008).[10] (Brown 1995) wrote that the "major methodological innovation in the general equilibrium analysis of firms with pricing rules" was "the introduction of the methods of non-smooth analysis, as a [synthesis] of global analysis (differential topology) and [of] convex analysis." According to (Brown 1995), "Non-smooth analysis extends the local approximation of manifolds by tangent planes [and extends] the analogous approximation of convex sets by tangent cones to sets" that can be non-smooth or non-convex.[11][55]

See also

Notes

  1. ↑ 1.0 1.1 1.2 1.3 1.4 Mas-Colell, A. (1987). "Non-convexity". in Eatwell, John; Milgate, Murray; Newman, Peter. The New Palgrave: A Dictionary of Economics (first ed.). Palgrave Macmillan. pp. 653–661. doi:10.1057/9780230226203.3173. ISBN 9780333786765. http://www.econ.upf.edu/~mcolell/research/art_083b.pdf. 
  2. ↑ Green, Jerry; Heller, Walter P. (1981). "1 Mathematical analysis and convexity with applications to economics". in Arrow, Kenneth Joseph; Intriligator, Michael D.. Handbook of mathematical economics, Volume I. Handbooks in economics. 1. Amsterdam: North-Holland Publishing Co.. pp. 15–52. doi:10.1016/S1573-4382(81)01005-9. ISBN 0-444-86126-2. 
  3. ↑ 3.0 3.1 Salanié, Bernard (2000). "7 Nonconvexities". Microeconomics of market failures (English translation of the (1998) French Microéconomie: Les défaillances du marché (Economica, Paris) ed.). Cambridge, MA: MIT Press. pp. 107–125. ISBN 0-262-19443-0. 
  4. ↑ 4.0 4.1 4.2 (Salanié 2000)
  5. ↑ 5.0 5.1 5.2 Laffont, Jean-Jacques (1988). "3 Nonconvexities". Fondements de L'economie Publique. MIT. pp. 63–65. ISBN 0-262-12127-1. https://books.google.com/books?id=O5MnAQAAIAAJ&q=editions:ISBN%200-262-12127-1. 
  6. ↑ 6.0 6.1 6.2 Starrett, David A. (1972). "Fundamental nonconvexities in the theory of externalities". Journal of Economic Theory 4 (2): 180–199. doi:10.1016/0022-0531(72)90148-2. 
  7. ↑ 7.0 7.1 7.2 Pages 106, 110–137, 172, and 248: Baumol, William J.; Oates, Wallace E.; with contributions by V. S. Bawa and David F. Bradford (1988). "8 Detrimental externalities and nonconvexities in the production set". The Theory of environmental policy (Second ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-31112-0. 
  8. ↑ 8.0 8.1 8.2 8.3 8.4 Page 1: Guesnerie, Roger (1975). "Pareto optimality in non-convex economies". Econometrica 43 (1): 1–29. doi:10.2307/1913410.  ("Errata". Econometrica 43 (5–6): p. 1010. 1975. doi:10.2307/1911353. )
  9. ↑ 9.0 9.1 Mordukhovich, Boris S. (2006). "Chapter 8 Applications to economics". Variational analysis and generalized differentiation II: Applications. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. 331. Springer. especially Section 8.5.3 "Enter nonconvexity" (and the remainder of the chapter), particularly page 495. ISBN 978-3-540-25438-6. 
  10. ↑ 10.0 10.1 Khan, M. Ali (2008). "Perfect competition". in Durlauf, Steven N.; Blume, Lawrence E.. The New Palgrave Dictionary of Economics (Second ed.). Palgrave Macmillan. pp. 354–365. doi:10.1057/9780230226203.1267. ISBN 978-0-333-78676-5. http://www.dictionaryofeconomics.com/article?id=pde2008_P000056. 
  11. ↑ 11.0 11.1 Brown, Donald J. (1991). "36 Equilibrium analysis with non-convex technologies". in Hildenbrand, Werner; Sonnenschein, Hugo. Handbook of mathematical economics, Volume IV. Handbooks in Economics. 1. Amsterdam: North-Holland Publishing Co. pp. 1963–1995 [1966]. doi:10.1016/S1573-4382(05)80011-6. ISBN 0-444-87461-5. 
  12. ↑ (Hotelling 1935): Hotelling, Harold (January 1935). "Demand functions with limited budgets". Econometrica 3 (1): 66–78. doi:10.2307/1907346. 
  13. ↑ Pages 231 and 239 (Figure 10 a–b: Illustration of lemma 5 [page 240]): Wold, Herman (1943b). "A synthesis of pure demand analysis II". Skandinavisk Aktuarietidskrift [Scandinavian Actuarial Journal] 26: pp. 220–263. 

    Exercise 45, page 146: Wold, Herman; Juréen, Lars (in association with Wold) (1953). "8 Some further applications of preference fields (pp. 129–148)". Demand analysis: A study in econometrics. Wiley publications in statistics. New York: John Wiley and Sons, Inc. Stockholm: Almqvist and Wiksell. 
  14. ↑ (Samuelson 1950):

    It will be noted that any point where the indifference curves are convex rather than concave cannot be observed in a competitive market. Such points are shrouded in eternal darkness—unless we make our consumer a monopsonist and let him choose between goods lying on a very convex "budget curve" (along which he is affecting the price of what he buys). In this monopsony case, we could still deduce the slope of the man's indifference curve from the slope of the observed constraint at the equilibrium point.

    For the epigraph to their seventh chapter, "Markets with non-convex preferences and production" presenting (Starr 1969), (Arrow Hahn) quote John Milton's description of the (non-convex) Serbonian Bog in Paradise Lost (Book II, lines 592–594):

    A gulf profound as that Serbonian Bog

    Betwixt Damiata and Mount Casius old,

    Where Armies whole have sunk.
  15. ↑ (Diewert 1982).
  16. ↑ Farrell, M. J. (August 1959). "The Convexity assumption in the theory of competitive markets". The Journal of Political Economy 67 (4): 371–391. doi:10.1086/258197.  Farrell, M. J. (October 1961a). "On Convexity, efficiency, and markets: A Reply". Journal of Political Economy 69 (5): 484–489. doi:10.1086/258541.  Farrell, M. J. (October 1961b). "The Convexity assumption in the theory of competitive markets: Rejoinder". Journal of Political Economy 69 (5): 493. doi:10.1086/258544. 
  17. ↑ Bator, Francis M. (October 1961a). "On convexity, efficiency, and markets". The Journal of Political Economy 69 (5): 480–483. doi:10.1086/258540.  Bator, Francis M. (October 1961b). "On convexity, efficiency, and markets: Rejoinder". Journal of Political Economy 69 (5): 489. doi:10.1086/258542. 
  18. ↑ Koopmans, Tjalling C. (October 1961). "Convexity assumptions, allocative efficiency, and competitive equilibrium". The Journal of Political Economy 69 (5): 478–479. doi:10.1086/258539. 

    (Koopmans 1961) and others—for example, (Farrell 1959) and (Farrell 1961a), (Bator 1961a), (Rothenberg 1960), and (Starr 1969)—commented on (Koopmans 1957):

    Koopmans, Tjalling C. (1957). "Allocation of resources and the price system". in Koopmans, Tjalling C. Three essays on the state of economic science. New York: McGraw–Hill Book Company. pp. 1–126. ISBN 0-07-035337-9. 
  19. ↑ (Rothenberg 1960): Rothenberg, Jerome (October 1960). "Non-convexity, aggregation, and Pareto optimality". The Journal of Political Economy 68 (5): 435–468. doi:10.1086/258363.  (Rothenberg, Jerome (October 1961). "Comments on non-convexity". Journal of Political Economy 69 (5): 490–492. doi:10.1086/258543. )
  20. ↑ (Arrow Hahn)
  21. ↑ (Shapley Shubik): Shapley, L. S.; Shubik, M. (October 1966). "Quasi-cores in a monetary economy with nonconvex preferences". Econometrica 34 (4): 805–827. doi:10.2307/1910101. 
  22. ↑ (Aumann 1966): Aumann, Robert J. (January 1966). "Existence of competitive equilibrium in markets with a continuum of traders". Econometrica 34 (1): 1–17. doi:10.2307/1909854.  (Aumann 1966) builds on two papers: Aumann (1964, 1965)

    Aumann, Robert J. (January–April 1964). "Markets with a continuum of traders". Econometrica 32 (1–2): 39–50. doi:10.2307/1913732. 

    Aumann, Robert J. (August 1965). "Integrals of set-valued functions". Journal of Mathematical Analysis and Applications 12 (1): 1–12. doi:10.1016/0022-247X(65)90049-1. 

  23. ↑ Taking the convex hull of non-convex preferences had been discussed earlier by (Wold 1943b) and by (Wold Juréen), according to (Diewert 1982).
  24. ↑ Pages 392–399 and page 188: Arrow, Kenneth J.; Hahn, Frank H. (1971). "Appendix B: Convex and related sets". General competitive analysis. Mathematical economics texts [Advanced textbooks in economics]. San Francisco, CA: Holden-Day, Inc. [North-Holland]. pp. 375–401. ISBN 0-444-85497-5. https://archive.org/details/generalcompetiti0000arro. 

    Pages 52–55 with applications on pages 145–146, 152–153, and 274–275: Mas-Colell, Andreu (1985). "1.L Averages of sets". The Theory of General Economic Equilibrium: A Differentiable Approach. Econometric Society Monographs. Cambridge University Press. ISBN 0-521-26514-2. 

    Theorem C(6) on page 37 and applications on pages 115-116, 122, and 168: Hildenbrand, Werner (1974). Core and equilibria of a large economy. Princeton studies in mathematical economics. Princeton, NJ: Princeton University Press. ISBN 978-0-691-04189-6. 

  25. ↑ Varian, Hal R. (1992). "21.2 Convexity and size". Microeconomic Analysis (3rd ed.). W. W. Norton & Company. pp. 393–394. ISBN 978-0-393-95735-8. https://archive.org/details/microeconomicana00vari_0/page/393. 

    Page 628: Mas–Colell, Andreu; Whinston, Michael D.; Green, Jerry R. (1995). "17.1 Large economies and nonconvexities". Microeconomic theory. Oxford University Press. pp. 627–630. ISBN 978-0-19-507340-9. 
  26. ↑ Page 169 in the first edition: Starr, Ross M. (2011). "8 Convex sets, separation theorems, and non-convex sets in RN". General equilibrium theory: An introduction (Second ed.). Cambridge: Cambridge University Press. doi:10.1017/CBO9781139174749. ISBN 978-0-521-53386-7. [clarification needed]

    (Ellickson 1994), and especially Chapter 7 "Walras meets Nash" (especially section 7.4 "Nonconvexity" pages 306–310 and 312, and also 328–329) and Chapter 8 "What is Competition?" (pages 347 and 352): Ellickson, Bryan (1994). Competitive equilibrium: Theory and applications. Cambridge University Press. ISBN 978-0-521-31988-1. 

  27. ↑ Theorem 1.6.5 on pages 24–25: Ichiishi, Tatsuro (1983). Game theory for economic analysis. Economic theory, econometrics, and mathematical economics. New York: Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers]. ISBN 0-12-370180-5. 
  28. ↑ Cassels, J. W. S. (1981). "Appendix A Convex sets". Economics for mathematicians. London Mathematical Society lecture note series. 62. Cambridge, New York: Cambridge University Press. pp. 33–34 and 127. ISBN 0-521-28614-X. 
  29. ↑ Pages 93–94 (especially example 1.92), 143, 318–319, 375–377, and 416: Carter, Michael (2001). Foundations of mathematical economics. Cambridge, MA: MIT Press. ISBN 0-262-53192-5. 

    Page 309: Moore, James C. (1999). Mathematical methods for economic theory: Volume I. Studies in economic theory. 9. Berlin: Springer-Verlag. doi:10.1007/978-3-662-08544-8. ISBN 3-540-66235-9. 

    Pages 47–48: Florenzano, Monique; Le Van, Cuong (2001). Finite dimensional convexity and optimization. Studies in economic theory. 13. in cooperation with Pascal Gourdel. Berlin: Springer-Verlag. doi:10.1007/978-3-642-56522-9. ISBN 3-540-41516-5. 
  30. ↑ Economists have studied non-convex sets using advanced mathematics, particularly differential geometry and topology, Baire category, measure and integration theory, and ergodic theory: Trockel, Walter (1984). Market demand: An analysis of large economies with nonconvex preferences. Lecture Notes in Economics and Mathematical Systems. 223. Berlin: Springer-Verlag. doi:10.1007/978-3-642-46488-1. ISBN 3-540-12881-6. 
  31. ↑ Sraffa, Piero (1926). "The Laws of returns under competitive conditions". Economic Journal 36 (144): pp. 535–550. 
  32. ↑ Hotelling, Harold (July 1938). "The General welfare in relation to problems of taxation and of railway and utility rates". Econometrica 6 (3): 242–269. doi:10.2307/1907054. 
  33. ↑ Pages 5–7: Quinzii, Martine (1992). Increasing returns and efficiency (Revised translation of (1988) Rendements croissants et efficacité economique. Paris: Editions du Centre National de la Recherche Scientifique ed.). New York: Oxford University Press. ISBN 0-19-506553-0. 
  34. ↑ Starrett discusses non-convexities in his textbook on public economics (pages 33, 43, 48, 56, 70–72, 82, 147, and 234–236): Starrett, David A. (1988). Foundations of public economics. Cambridge economic handbooks. Cambridge: Cambridge University Press. ISBN 9780521348010. https://books.google.com/books?id=R35yljdyyIkC&q=nonconvex+OR+nonconvexities&pg=PR11. 
  35. ↑ Radner, Roy (1968). "Competitive equilibrium under uncertainty". Econometrica 36 (1): 31–53. doi:10.2307/1909602. 
  36. ↑ Page 270: Drèze, Jacques H.. "14 Investment under private ownership: Optimality, equilibrium and stability". in Drèze, J. H.. Essays on economic decisions under uncertainty. Cambridge University Press. doi:10.1017/CBO9780511559464. ISBN 0-521-26484-7.  (Originally published as Drèze, Jacques H. (1974). "Investment under private ownership: Optimality, equilibrium and stability". in Drèze, J. H.. Allocation under Uncertainty: Equilibrium and Optimality. New York: Wiley. pp. 129–165. )
  37. ↑ (Magille Quinzii): Magill, Michael; Quinzii, Martine (1996). "6 Production in a finance economy". The Theory of incomplete markets. Cambridge, Massachusetts: MIT Press. pp. 329–425. 
  38. ↑ Ramsey, F. P. (1928). "A Mathematical Theory of Saving". Economic Journal 38 (152): 543–559. doi:10.2307/2224098. 
  39. ↑ Hotelling, Harold (1931). "The Economics of Exhaustible Resources". Journal of Political Economy 39 (2): 137–175. doi:10.1086/254195. http://www.e-elgar.com/shop/isbn/9781852785802. 
  40. ↑ Adda, Jerome; Cooper, Russell (2003), Dynamic Economics, MIT Press, http://www.eco.utexas.edu/~cooper/dynprog/dynprog1.html, retrieved 2011-03-01 
  41. ↑ Howard, Ronald A. (1960). Dynamic Programming and Markov Processes. The M.I.T. Press. 
  42. ↑ Sethi, S. P.; Thompson, G. L. (2000). Optimal Control Theory: Applications to Management Science and Economics (2nd ed.). Berlin: Springer. ISBN 0-387-28092-8.  Slides are available at http://www.utdallas.edu/~sethi/OPRE7320presentation.html
  43. ↑ Troutman, John L. (1996). With the assistance of William Hrusa. ed. Variational calculus and optimal control: Optimization with elementary convexity. Undergraduate Texts in Mathematics (Second ed.). New York: Springer-Verlag. doi:10.1007/978-1-4612-0737-5. ISBN 0-387-94511-3. 
  44. ↑ Craven, B. D. (1995). Control and optimization. Chapman and Hall Mathematics Series. London: Chapman and Hall, Ltd.. doi:10.1007/978-1-4899-7226-2. ISBN 0-412-55890-4. https://archive.org/details/controloptimizat0000crav. 
  45. ↑ Vinter, Richard (2000). Optimal control. Systems & Control: Foundations & Applications. Boston, MA: Birkhäuser Boston, Inc.. ISBN 0-8176-4075-4. 
  46. ↑ Beckmann, Martin; Muth, Richard F. (1954). "On the solution to the fundamental equation of inventory theory". Cowles Commission Discussion Paper 2116. 
  47. ↑ Merton, Robert C. (1973). "An Intertemporal Capital Asset Pricing Model". Econometrica 41 (5): 867–887. doi:10.2307/1913811. 
  48. ↑ Stokey, Nancy; Lucas, Robert E.; Prescott, Edward (1989). Recursive Methods in Economic Dynamics. Harvard Univ. Press. ISBN 0-674-75096-9. 
  49. ↑ Ljungqvist, Lars; Sargent, Thomas (2004). Recursive Macroeconomic Theory. MIT Press. ISBN 0-262-12274-X. 
  50. ↑ Dixit, Avinash; Pindyck, Robert (1994). Investment Under Uncertainty. Princeton Univ. Press. ISBN 0-691-03410-9. https://archive.org/details/investmentunderu00dixi_0. 
  51. ↑ (Dasgupta Heal)
  52. ↑ (Dasgupta Heal)
  53. ↑ (Heal 1999): Heal, G. M. (1999). "Introduction". The economics of increasing returns. The International Library of Critical Writings in Economics. Edward Elgar. ISBN 978-1-85898-160-4. http://www2.gsb.columbia.edu/faculty/gheal/EconomicTheoryPapers/pw-97-20.pdf. Retrieved 5 March 2011. 
  54. ↑ Rockafellar, R. Tyrrell; Wets, Roger J-B (1998). Variational analysis. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. 317. Berlin: Springer-Verlag. doi:10.1007/978-3-642-02431-3. ISBN 3-540-62772-3. 
  55. ↑ Algebraic topology has also been used to study convex and non-convex sets in economics:Chichilnisky, G. (1993). "Intersecting families of sets and the topology of cones in economics". Bulletin of the American Mathematical Society. New Series 29 (2): 189–207. doi:10.1090/S0273-0979-1993-00439-7. https://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00439-7/S0273-0979-1993-00439-7.pdf. 

References

External links

Heal, G. M. (April 1998). The Economics of Increasing Returns. PaineWebber working paper series in money, economics, and finance. Columbia Business School. PW-97-20. http://www2.gsb.columbia.edu/faculty/gheal/EconomicTheoryPapers/pw-97-20.pdf. Retrieved 5 March 2011. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Finance:Non-convexity_(economics)&oldid=3318281"