Proofs of quadratic reciprocity
In number theory, the law of quadratic reciprocity, like the Pythagorean theorem, has lent itself to an unusually large number of proofs. Several hundred proofs of the law of quadratic reciprocity have been published.
Proof synopsis
Of the elementary combinatorial proofs, there are two which apply types of double counting. One by Gotthold Eisenstein counts lattice points. Another applies Zolotarev's lemma to [math]\displaystyle{ (\mathbb{Z}/pq\mathbb{Z})^{\times} }[/math], expressed by the Chinese remainder theorem as [math]\displaystyle{ (\mathbb{Z} /p \mathbb{Z})^{\times} \times (\mathbb{Z} /q \mathbb{Z})^{\times} }[/math] and calculates the signature of a permutation. The shortest known proof also uses a simplified version of double counting, namely double counting modulo a fixed prime.
Eisenstein's proof
Eisenstein's proof of quadratic reciprocity is a simplification of Gauss's third proof. It is more geometrically intuitive and requires less technical manipulation.
The point of departure is "Eisenstein's lemma", which states that for distinct odd primes p, q,
- [math]\displaystyle{ \left(\frac qp\right) = (-1)^{\sum_u \left \lfloor qu/p \right \rfloor}, }[/math]
where [math]\displaystyle{ \left \lfloor x \right \rfloor }[/math] denotes the floor function (the largest integer less than or equal to x), and where the sum is taken over the even integers u = 2, 4, 6, ..., p−1. For example,
- [math]\displaystyle{ \left(\frac 7{11}\right) = (-1)^{ \left \lfloor 14/11 \right \rfloor + \left \lfloor 28/11 \right \rfloor + \left \lfloor 42/11 \right \rfloor + \left \lfloor 56/11 \right \rfloor + \left \lfloor 70/11 \right \rfloor } = (-1)^{1 + 2 + 3 + 5 + 6} = (-1)^{17} = -1. }[/math]
This result is very similar to Gauss's lemma, and can be proved in a similar fashion (proof given below).
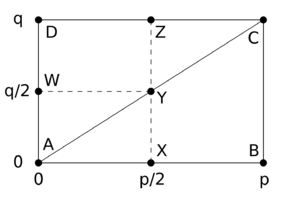
Using this representation of (q/p), the main argument is quite elegant. The sum [math]\displaystyle{ \sum_u \left \lfloor qu/p \right \rfloor }[/math] counts the number of lattice points with even x-coordinate in the interior of the triangle ABC in the following diagram:
Because each column has an even number of points (namely q−1 points), the number of such lattice points in the region BCYX is the same modulo 2 as the number of such points in the region CZY:
Then by flipping the diagram in both axes, we see that the number of points with even x-coordinate inside CZY is the same as the number of points inside AXY having odd x-coordinates. This can be justified mathematically by noting that [math]\displaystyle{ \textstyle q-1-\left\lfloor \frac{2kq}{p}\right\rfloor = \left\lfloor\frac{(p-2k)q}{p}\right\rfloor }[/math].[1]
The conclusion is that
- [math]\displaystyle{ \left(\frac qp\right) = (-1)^\mu, }[/math]
where μ is the total number of lattice points in the interior of AXY.
Switching p and q, the same argument shows that
- [math]\displaystyle{ \left(\frac pq\right) = (-1)^\nu, }[/math]
where ν is the number of lattice points in the interior of WYA. Since there are no lattice points on the line AY itself (because p and q are relatively prime), and since the total number of points in the rectangle WYXA is
- [math]\displaystyle{ \left(\frac{p-1}2\right) \left(\frac{q-1}2\right), }[/math]
we obtain
- [math]\displaystyle{ \left(\frac qp\right) \left(\frac pq\right) = (-1)^{\mu + \nu} = (-1)^{(p-1)(q-1)/4}. }[/math]
Proof of Eisenstein's lemma
For an even integer u in the range 1 ≤ u ≤ p−1, denote by r(u) the least positive residue of qu modulo p. (For example, for p = 11, q = 7, we allow u = 2, 4, 6, 8, 10, and the corresponding values of r(u) are 3, 6, 9, 1, 4.) The numbers (−1)r(u)r(u), again treated as least positive residues modulo p, are all even (in our running example, they are 8, 6, 2, 10, 4.) Furthermore, they are all distinct, because if (−1)r(u)r(u) ≡ (−1)r(t)r(t) (mod p), then we may divide out by q to obtain u ≡ ±t (mod p). This forces u ≡ t (mod p), because both u and t are even, whereas p is odd. Since there exactly (p−1)/2 of them and they are distinct, they must be simply a rearrangement of the even integers 2, 4, ..., p−1. Multiplying them together, we obtain
- [math]\displaystyle{ (-1)^{r(2)}2q \cdot (-1)^{r(4)}4q \cdot \cdots \cdot (-1)^{r(p-1)}(p-1)q \equiv 2 \cdot 4 \cdot \cdots \cdot (p-1)\pmod{p}. }[/math]
Dividing out successively by 2, 4, ..., p−1 on both sides (which is permissible since none of them are divisible by p) and rearranging, we have
- [math]\displaystyle{ q^{(p-1)/2} \equiv (-1)^{r(2) + r(4) + \cdots + r(p-1)}\pmod{p}. }[/math]
On the other hand, by the definition of r(u) and the floor function,
- [math]\displaystyle{ \frac{qu}p = \left \lfloor \frac{qu}p\right \rfloor + \frac{r(u)}p, }[/math]
and since p is odd and u is even,
- [math]\displaystyle{ qu = p\left\lfloor\frac{qu}p\right\rfloor + r(u) }[/math]
implies that [math]\displaystyle{ \left \lfloor qu/p \right \rfloor }[/math] and r(u) are congruent modulo 2.
Finally this shows that
- [math]\displaystyle{ q^{(p-1)/2} \equiv (-1)^{\sum_u \left \lfloor qu/p \right \rfloor} \pmod{p}. }[/math]
We are finished because the left hand side is just an alternative expression for (q/p).
Addendum to the lemma
This lemma essentially states that the number of least residues after doubling that are odd gives the value of (q/p). This follows easily from Gauss' lemma.
Also, [math]\displaystyle{ qu = p\left\lfloor\frac{qu}p\right\rfloor + r(u) }[/math] implies that [math]\displaystyle{ \left \lfloor qu/p \right \rfloor }[/math] and r(u) are either congruent modulo 2, or incongruent, depending solely on the parity of u.
This means that the residues [math]\displaystyle{ 1,2,\dots,\frac{p-1}{2} }[/math] are (in)congruent to [math]\displaystyle{ \left \lfloor qu/p \right \rfloor }[/math], and so
[math]\displaystyle{ (-1)^{\frac{p-1}{2}}\equiv (-1)^{\sum_u \left \lfloor qu/p \right \rfloor}\equiv (-1)^{\sum_u r(u)+u} }[/math]
where [math]\displaystyle{ \textstyle 1\le u\le \frac{p-1}{2} }[/math].
For example, using the previous example of [math]\displaystyle{ p=7, q=11 }[/math], the residues are [math]\displaystyle{ 7,3,10,6,2 }[/math] and the floor function gives [math]\displaystyle{ 0,1,1,2,3 }[/math]. The pattern of congruence is [math]\displaystyle{ 1,0,1,0,1 }[/math].
Proof using quadratic Gauss sums
The proof of Quadratic Reciprocity using Gauss sums is one of the more common and classic proofs. These proofs work by comparing computations of single values in two different ways, one using Euler's Criterion and the other using the Binomial theorem. As an example of how Euler's criterion is used, we can use it to give a quick proof of the first supplemental case of determining [math]\displaystyle{ \left(\frac{-1}{p}\right) }[/math] for an odd prime p: By Euler's criterion [math]\displaystyle{ \left(\frac{-1}{p}\right) \equiv (-1)^{\frac{p-1}{2}} \pmod{p} }[/math] , but since both sides of the equivalence are ±1 and p is odd, we can deduce that [math]\displaystyle{ \left(\frac{-1}{p}\right) = (-1)^{\frac{p-1}{2}} }[/math].
The second supplemental case
Let [math]\displaystyle{ \zeta_8 = e^{2\pi i/8} }[/math], a primitive 8th root of unity and set [math]\displaystyle{ \tau = \zeta_8+\zeta_8^{-1} }[/math]. Since [math]\displaystyle{ \zeta_8^2 = i }[/math] and [math]\displaystyle{ \zeta_8^{-2}=-i }[/math] we see that [math]\displaystyle{ \tau^{2} = 2 }[/math]. Because [math]\displaystyle{ \tau }[/math] is an algebraic integer, if p is an odd prime it makes sense to talk about it modulo p. (Formally we are considering the commutative ring formed by factoring the algebraic integers [math]\displaystyle{ \mathbf A }[/math] with the ideal generated by p. Because [math]\displaystyle{ p^{-1} }[/math] is not an algebraic integer, 1, 2, ..., p are distinct elements of [math]\displaystyle{ {\mathbf A}/p{\mathbf A} }[/math].) Using Euler's criterion, it follows that [math]\displaystyle{ \tau^{p-1} =(\tau^2)^{\frac{p-1}{2}} = 2^{\frac{p-1}{2}} \equiv \left(\frac{2}{p}\right) \pmod{p} }[/math]We can then say that [math]\displaystyle{ \tau^p\equiv \left(\frac{2}{p}\right)\tau\pmod{p} }[/math]But we can also compute [math]\displaystyle{ \tau^p \pmod{p} }[/math] using the binomial theorem. Because the cross terms in the binomial expansion all contain factors of p, we find that [math]\displaystyle{ \tau^p\equiv \zeta_8^p+\zeta_8^{-p} \pmod{p} }[/math]. We can evaluate this more exactly by breaking this up into two cases
- [math]\displaystyle{ p\equiv \pm 1\pmod{8} \Rightarrow \zeta_8^p+\zeta_8^{-p} = \zeta_8+\zeta_8^{-1} }[/math].
- [math]\displaystyle{ p\equiv \pm 3 \pmod{8} \Rightarrow \zeta_8^p+\zeta_8^{-p} = -\zeta_8-\zeta_8^{-1} }[/math].
These are the only options for a prime modulo 8 and both of these cases can be computed using the exponential form [math]\displaystyle{ \zeta_8=e^{\frac{2\pi i}{8}} }[/math]. We can write this succinctly for all odd primes p as [math]\displaystyle{ \tau^p \equiv (-1)^{\frac{p^2-1}{8}}\tau \pmod{p} }[/math]Combining these two expressions for [math]\displaystyle{ \tau^p\pmod{p} }[/math] and multiplying through by [math]\displaystyle{ \tau }[/math] we find that [math]\displaystyle{ 2\cdot \left(\frac{2}{p}\right) \equiv 2\cdot(-1)^{\frac{p^2-1}{8}}\pmod{p} }[/math]. Since both [math]\displaystyle{ \left(\frac{2}{p}\right) }[/math] and [math]\displaystyle{ (-1)^{\frac{p^2-1}{8}} }[/math] are ±1 and 2 is invertible modulo p, we can conclude that [math]\displaystyle{ \left(\frac{2}{p}\right) = (-1)^{\frac{p^2-1}{8}} }[/math]
The general case
The idea for the general proof follows the above supplemental case: Find an algebraic integer that somehow encodes the Legendre symbols for p, then find a relationship between Legendre symbols by computing the qth power of this algebraic integer modulo q in two different ways, one using Euler's criterion the other using the binomial theorem.
Let [math]\displaystyle{ g_p = \sum_{k=1}^{p-1}\left(\frac{k}{p}\right)\zeta_p^k }[/math]where [math]\displaystyle{ \zeta_p=e^{2\pi i/p} }[/math] is a primitive pth root of unity. This is a quadratic Gauss sum. A fundamental property of these Gauss sums is that [math]\displaystyle{ g_p^2 = p^* }[/math]where [math]\displaystyle{ p^*=\left(\frac{-1}{p}\right) p }[/math]. To put this in context of the next proof, the individual elements of the Gauss sum are in the cyclotomic field [math]\displaystyle{ L = \mathbb{Q}(\zeta_p) }[/math] but the above formula shows that the sum itself is a generator of the unique quadratic field contained in L. Again, since the quadratic Gauss sum is an algebraic integer, we can use modular arithmetic with it. Using this fundamental formula and Euler's criterion we find that[math]\displaystyle{ g_p^{q-1} = (g_p^2)^{\frac{q-1}{2}} = (p^*)^{\frac{q-1}{2}} \equiv \left(\frac{p^*}{q}\right)\pmod{q} }[/math]Therefore[math]\displaystyle{ g_p^q \equiv \left(\frac{p^*}{q}\right)g_p\pmod{q} }[/math]Using the binomial theorem, we also find that [math]\displaystyle{ g_p^q\equiv\sum_{k=1}^{p-1}\left(\frac{k}{p}\right)\zeta_p^{qk} \pmod{q} }[/math], If we let a be a multiplicative inverse of [math]\displaystyle{ q\pmod{p} }[/math], then we can rewrite this sum as [math]\displaystyle{ \left(\frac{a}{p}\right)\sum_{t=1}^{p-1}\left(\frac{t}{p}\right)\zeta_p^t }[/math] using the substitution [math]\displaystyle{ t=qk }[/math], which doesn't affect the range of the sum. Since [math]\displaystyle{ \left(\frac{a}{p}\right)=\left(\frac{q}{p}\right) }[/math], we can then write[math]\displaystyle{ g_p^q\equiv\left(\frac{q}{p}\right)g_p\pmod{q} }[/math]Using these two expressions for [math]\displaystyle{ g_p^q \pmod{q} }[/math], and multiplying through by [math]\displaystyle{ g_p }[/math] gives[math]\displaystyle{ \left(\frac{q}{p}\right)p^*\equiv \left(\frac{p^*}{q}\right)p^*\pmod{q} }[/math]Since [math]\displaystyle{ p^* }[/math] is invertible modulo q, and the Legendre symbols are either ±1, we can then conclude that[math]\displaystyle{ \left(\frac{q}{p}\right) = \left(\frac{p^*}{q}\right) }[/math]
Proof using algebraic number theory
The proof presented here is by no means the simplest known; however, it is quite a deep one, in the sense that it motivates some of the ideas of Artin reciprocity.
Cyclotomic field setup
Suppose that p is an odd prime. The action takes place inside the cyclotomic field [math]\displaystyle{ L = \mathbb Q(\zeta_p), }[/math] where ζp is a primitive pth root of unity. The basic theory of cyclotomic fields informs us that there is a canonical isomorphism
- [math]\displaystyle{ G = \operatorname{Gal}(L/\mathbb Q) \cong (\Z/p\Z)^\times }[/math]
which sends the automorphism σa satisfying [math]\displaystyle{ \sigma_a(\zeta_p) = \zeta_p^a }[/math] to the element [math]\displaystyle{ a \in (\Z/p\Z)^\times. }[/math] In particular, this isomorphism is injective because the multiplicative group of a field is a cyclic group: [math]\displaystyle{ F^\times\cong C_{p-1} }[/math].
Now consider the subgroup H of squares of elements of G. Since G is cyclic, H has index 2 in G, so the subfield corresponding to H under the Galois correspondence must be a quadratic extension of Q. (In fact it is the unique quadratic extension of Q contained in L.) The Gaussian period theory determines which one; it turns out to be [math]\displaystyle{ \mathbb Q(\sqrt{p^*}) }[/math], where
- [math]\displaystyle{ p^* = \left\{\begin{array}{rl} p & \text{if } p \equiv 1 \pmod{4}, \\ -p & \text{if } p \equiv 3 \pmod{4}. \end{array}\right. }[/math]
At this point we start to see a hint of quadratic reciprocity emerging from our framework. On one hand, the image of H in [math]\displaystyle{ (\mathbb Z/p\mathbb Z)^\times }[/math] consists precisely of the (nonzero) quadratic residues modulo p. On the other hand, H is related to an attempt to take the square root of p (or possibly of −p). In other words, if now q is a prime (different from p), we have shown that
- [math]\displaystyle{ \left(\frac qp\right) =1 \quad \iff \quad \sigma_q \in H \quad \iff \quad \sigma_q \mbox{ fixes } \mathbb Q(\sqrt{p^*}). }[/math]
The Frobenius automorphism
In the ring of integers [math]\displaystyle{ \mathcal O_L=\mathbb Z[\zeta_p] }[/math], choose any unramified prime ideal β of lying over q, and let [math]\displaystyle{ \phi \in \operatorname{Gal}(L/\mathbb Q) }[/math] be the Frobenius automorphism associated to β; the characteristic property of [math]\displaystyle{ \phi }[/math] is that
- [math]\displaystyle{ \phi(x) \equiv x^q\!\!\! \pmod{\beta}\ \text{ for any } x\in \mathcal O_L. }[/math]
(The existence of such a Frobenius element depends on quite a bit of algebraic number theory machinery.)
The key fact about [math]\displaystyle{ \phi }[/math] that we need is that for any subfield K of L,
- [math]\displaystyle{ \phi\,\mbox{ fixes } K \quad \iff \quad q\,\mbox{ splits completely in } K. }[/math]
Indeed, let δ be any ideal of OK below β (and hence above q). Then, since [math]\displaystyle{ \phi(x) \equiv x^q\!\!\! \pmod{\delta} }[/math] for any [math]\displaystyle{ x\in \mathcal O_K }[/math], we see that [math]\displaystyle{ \phi\vert_K \in \operatorname{Gal}(K/\mathbb Q) }[/math] is a Frobenius for δ. A standard result concerning [math]\displaystyle{ \phi }[/math] is that its order is equal to the corresponding inertial degree; that is,
- [math]\displaystyle{ \operatorname{ord}(\phi\vert_K) = [O_K/\delta O_K : \mathbb Z/q\mathbb Z]. }[/math]
The left hand side is equal to 1 if and only if φ fixes K, and the right hand side is equal to one if and only q splits completely in K, so we are done.
Now, since the pth roots of unity are distinct modulo β (i.e. the polynomial Xp − 1 is separable in characteristic q), we must have
- [math]\displaystyle{ \phi(\zeta_p) = \zeta_p^q; }[/math]
that is, [math]\displaystyle{ \phi }[/math] coincides with the automorphism σq defined earlier. Taking K to be the quadratic field in which we are interested, we obtain the equivalence
- [math]\displaystyle{ \left(\frac qp\right) =1 \quad \iff \quad q\,\mbox{ splits completely in } \mathbb Q(\sqrt{p^*}). }[/math]
Completing the proof
Finally we must show that
- [math]\displaystyle{ q\,\mbox{ splits completely in } \mathbb Q(\sqrt{p^*}) \quad \iff \quad \left(\frac{p^*}q\right) = 1. }[/math]
Once we have done this, the law of quadratic reciprocity falls out immediately since
- [math]\displaystyle{ \left(\frac{p^*}q\right) = \left(\frac pq\right)\ \text{ for } p\equiv 1\!\!\! \pmod 4, }[/math]
and
- [math]\displaystyle{ \left(\frac{p^*}q\right) = \left(\frac{-p}q\right) = \left(\frac{-1}q\right)\left(\frac pq\right) = \begin{cases} +\left(\frac pq \right) & \mbox{if } q \equiv 1 \pmod{4}, \\ -\left(\frac pq\right) & \mbox{if } q \equiv 3 \pmod{4}\end{cases} }[/math]
for [math]\displaystyle{ p\equiv 3\!\!\! \pmod 4 }[/math].
To show the last equivalence, suppose first that [math]\displaystyle{ \left(\frac{p^*}q\right) = 1. }[/math] In this case, there is some integer x (not divisible by q) such that [math]\displaystyle{ x^2 \equiv p^* \pmod{q}, }[/math] say [math]\displaystyle{ x^2 - p^* = cq }[/math] for some integer c. Let [math]\displaystyle{ K = \mathbb Q(\sqrt{p^*}), }[/math] and consider the ideal [math]\displaystyle{ (x-\sqrt{p^*},q) }[/math] of K. It certainly divides the principal ideal (q). It cannot be equal to (q), since [math]\displaystyle{ x-\sqrt{p^*} }[/math] is not divisible by q. It cannot be the unit ideal, because then
- [math]\displaystyle{ (x+\sqrt{p^*}) = (x+\sqrt{p^*})(x-\sqrt{p^*},q) = (cq, q(x+\sqrt{p^*})) }[/math]
is divisible by q, which is again impossible. Therefore (q) must split in K.
Conversely, suppose that (q) splits, and let β be a prime of K above q. Then [math]\displaystyle{ (q) \subsetneq \beta, }[/math] so we may choose some
- [math]\displaystyle{ a+b\sqrt{p^*} \in \beta\setminus(q), \text{ where } a,b\in \mathbb Q. }[/math]
Actually, since [math]\displaystyle{ p^* \equiv 1\!\!\! \pmod{4}, }[/math] elementary theory of quadratic fields implies that the ring of integers of K is precisely [math]\displaystyle{ \mathbb Z\left[\frac{1+\sqrt{p^*}}2\right], }[/math] so the denominators of a and b are at worst equal to 2. Since q ≠ 2, we may safely multiply a and b by 2, and assume that [math]\displaystyle{ a+b\sqrt{p^*} \in \beta\setminus(q), }[/math] where now a and b are in Z. In this case we have
- [math]\displaystyle{ (a+b\sqrt{p^*})(a-b\sqrt{p^*}) = a^2 - b^2p^* \in \beta \cap \mathbb Z = (q), }[/math]
so [math]\displaystyle{ q \mid a^2 - b^2p^*. }[/math] However, q cannot divide b, since then also q divides a, which contradicts our choice of [math]\displaystyle{ a+b\sqrt{p^*}. }[/math] Therefore, we may divide by b modulo q, to obtain [math]\displaystyle{ p^* \equiv (ab^{-1})^2\!\!\! \pmod{q} }[/math] as desired.
References
Every textbook on elementary number theory (and quite a few on algebraic number theory) has a proof of quadratic reciprocity. Two are especially noteworthy:
(Lemmermeyer 2000) has many proofs (some in exercises) of both quadratic and higher-power reciprocity laws and a discussion of their history. Its immense bibliography includes literature citations for 196 different published proofs.
(Ireland Rosen) also has many proofs of quadratic reciprocity (and many exercises), and covers the cubic and biquadratic cases as well. Exercise 13.26 (p 202) says it all
Count the number of proofs to the law of quadratic reciprocity given thus far in this book and devise another one.
- Ireland, Kenneth; Rosen, Michael (1990), A Classical Introduction to Modern Number Theory, Graduate Texts in Mathematics, Vol. 84 (2nd ed.), New York: Springer, ISBN 0-387-97329-X, https://www.springer.com/de/book/9780387973296
- Lemmermeyer, Franz (2000), Reciprocity Laws: from Euler to Eisenstein, Springer Monographs in Mathematics, Berlin: Springer, ISBN 3-540-66957-4, https://www.springer.com/de/book/9783540669579
- Rousseau, G. (1991), "On the Quadratic Reciprocity Law", Journal of the Australian Mathematical Society, Series A (Cambridge University Press) 51: 423–425, ISSN 1446-7887, http://journals.cambridge.org/download.php?file=%2FJAZ%2FJAZ1_51_03%2FS1446788700034583a.pdf&code=7681a6297e9c4a688a9e7b504bdd5319
- Washington, Lawrence C. (2012), Introduction to Cyclotomic Fields, Graduate Texts in Mathematics, 83 (2nd ed.), New York: Springer, ISBN 978-1-4612-7346-2, https://www.springer.com/de/book/9780387947624
External links
- F. Lemmermeyer's chronology and bibliography of proofs of the Quadratic Reciprocity Law (332 proofs)
 |