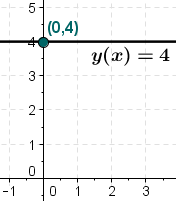Constant function
| Function | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x ↦ f (x) | |||||||||||||||||||||||||||||||||
| Examples by domain and codomain | |||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| Classes/properties | |||||||||||||||||||||||||||||||||
| Constant · Identity · Linear · Polynomial · Rational · Algebraic · Analytic · Smooth · Continuous · Measurable · Injective · Surjective · Bijective | |||||||||||||||||||||||||||||||||
| Constructions | |||||||||||||||||||||||||||||||||
| Restriction · Composition · λ · Inverse | |||||||||||||||||||||||||||||||||
| Generalizations | |||||||||||||||||||||||||||||||||
| Partial · Multivalued · Implicit | |||||||||||||||||||||||||||||||||
In mathematics, a constant function is a function whose (output) value is the same for every input value.[1][2][3] For example, the function y(x) = 4 is a constant function because the value of y(x) is 4 regardless of the input value x (see image).
Basic properties
As a real-valued function of a real-valued argument, a constant function has the general form y(x) = c or just y = c.[4]
- Example: The function y(x) = 2 or just y = 2 is the specific constant function where the output value is c = 2. The domain of this function is the set of all real numbers R. The image of this function is the singleton set {2}. The independent variable x does not appear on the right side of the function expression and so its value is "vacuously substituted". Namely y(0) = 2, y(−2.7) = 2, y(π) = 2, and so on. No matter what value of x is input, the output is 2.
- Real-world example: A store where every item is sold for the price of 1 dollar.
The graph of the constant function y = c is a horizontal line in the plane that passes through the point (0, c).[5]
In the context of a polynomial in one variable x, the non-zero constant function is a polynomial of degree 0 and its general form is f(x) = c where c is nonzero. This function has no intersection point with the x-axis, that is, it has no root (zero). On the other hand, the polynomial f(x) = 0 is the identically zero function. It is the (trivial) constant function and every x is a root. Its graph is the x-axis in the plane.[6]
A constant function is an even function, i.e. the graph of a constant function is symmetric with respect to the y-axis.
In the context where it is defined, the derivative of a function is a measure of the rate of change of function values with respect to change in input values. Because a constant function does not change, its derivative is 0.[7] This is often written: [math]\displaystyle{ (x \mapsto c)' = 0 }[/math]. The converse is also true. Namely, if y′(x) = 0 for all real numbers x, then y is a constant function.[8]
- Example: Given the constant function [math]\displaystyle{ y(x) = -\sqrt{2} }[/math]. The derivative of y is the identically zero function [math]\displaystyle{ y'(x) = \left(x \mapsto -\sqrt{2}\right)' = 0 }[/math].
Other properties
For functions between preordered sets, constant functions are both order-preserving and order-reversing; conversely, if f is both order-preserving and order-reversing, and if the domain of f is a lattice, then f must be constant.
- Every constant function whose domain and codomain are the same set X is a left zero of the full transformation monoid on X, which implies that it is also idempotent.
- It has zero slope or gradient.
- Every constant function between topological spaces is continuous.
- A constant function factors through the one-point set, the terminal object in the category of sets. This observation is instrumental for F. William Lawvere's axiomatization of set theory, the Elementary Theory of the Category of Sets (ETCS).[9]
- For any non-empty X, every set Y is isomorphic to the set of constant functions in [math]\displaystyle{ X \to Y }[/math]. For any X and each element y in Y, there is a unique function [math]\displaystyle{ \tilde{y}: X \to Y }[/math] such that [math]\displaystyle{ \tilde{y}(x) = y }[/math] for all [math]\displaystyle{ x \in X }[/math]. Conversely, if a function [math]\displaystyle{ f: X \to Y }[/math] satisfies [math]\displaystyle{ f(x) = f(x') }[/math] for all [math]\displaystyle{ x, x' \in X }[/math], [math]\displaystyle{ f }[/math] is by definition a constant function.
- As a corollary, the one-point set is a generator in the category of sets.
- Every set [math]\displaystyle{ X }[/math] is canonically isomorphic to the function set [math]\displaystyle{ X^1 }[/math], or hom set [math]\displaystyle{ \operatorname{hom}(1,X) }[/math] in the category of sets, where 1 is the one-point set. Because of this, and the adjunction between Cartesian products and hom in the category of sets (so there is a canonical isomorphism between functions of two variables and functions of one variable valued in functions of another (single) variable, [math]\displaystyle{ \operatorname{hom}(X \times Y, Z) \cong \operatorname{hom}(X(\operatorname{hom}(Y, Z)) }[/math]) the category of sets is a closed monoidal category with the Cartesian product of sets as tensor product and the one-point set as tensor unit. In the isomorphisms [math]\displaystyle{ \lambda: 1 \times X \cong X \cong X \times 1: \rho }[/math] natural in X, the left and right unitors are the projections [math]\displaystyle{ p_1 }[/math] and [math]\displaystyle{ p_2 }[/math] the ordered pairs [math]\displaystyle{ (*, x) }[/math] and [math]\displaystyle{ (x, *) }[/math] respectively to the element [math]\displaystyle{ x }[/math], where [math]\displaystyle{ * }[/math] is the unique point in the one-point set.
A function on a connected set is locally constant if and only if it is constant.
References
- ↑ Tanton, James (2005). Encyclopedia of Mathematics. Facts on File, New York. p. 94. ISBN 0-8160-5124-0.
- ↑ C.Clapham, J.Nicholson (2009). "Oxford Concise Dictionary of Mathematics, Constant Function". Addison-Wesley. p. 175. http://web.cortland.edu/matresearch/OxfordDictionaryMathematics.pdf.
- ↑ Weisstein, Eric (1999). CRC Concise Encyclopedia of Mathematics. CRC Press, London. p. 313. ISBN 0-8493-9640-9.
- ↑ Weisstein, Eric W.. "Constant Function" (in en). https://mathworld.wolfram.com/ConstantFunction.html.
- ↑ Dawkins, Paul (2007). "College Algebra". Lamar University. p. 224. http://tutorial.math.lamar.edu/Classes/Alg/Alg.aspx.
- ↑ Carter, John A.; Cuevas, Gilbert J.; Holliday, Berchie; Marks, Daniel; McClure, Melissa S. (2005). "1". Advanced Mathematical Concepts - Pre-calculus with Applications, Student Edition (1 ed.). Glencoe/McGraw-Hill School Pub Co. p. 22. ISBN 978-0078682278.
- ↑ Dawkins, Paul (2007). "Derivative Proofs". Lamar University. http://tutorial.math.lamar.edu/Classes/CalcI/DerivativeProofs.aspx.
- ↑ "Zero Derivative implies Constant Function". http://www.proofwiki.org/wiki/Zero_Derivative_implies_Constant_Function.
- ↑ Leinster, Tom (27 Jun 2011). "An informal introduction to topos theory". arXiv:1012.5647 [math.CT].
- Herrlich, Horst and Strecker, George E., Category Theory, Heldermann Verlag (2007).
External links
- Weisstein, Eric W.. "Constant Function". http://mathworld.wolfram.com/ConstantFunction.html.
- "Constant function". http://planetmath.org/?op=getobj&from=objects&id={{{id}}}.
 |