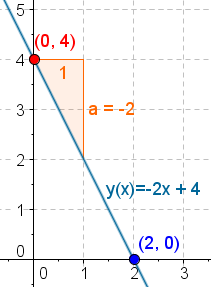Linear function (calculus)
In calculus and related areas of mathematics, a linear function from the real numbers to the real numbers is a function whose graph (in Cartesian coordinates) is a non-vertical line in the plane.[1] The characteristic property of linear functions is that when the input variable is changed, the change in the output is proportional to the change in the input.
Linear functions are related to linear equations.
Properties
A linear function is a polynomial function in which the variable x has degree at most one:[2]
- [math]\displaystyle{ f(x)=ax+b }[/math].
Such a function is called linear because its graph, the set of all points [math]\displaystyle{ (x,f(x)) }[/math] in the Cartesian plane, is a line. The coefficient a is called the slope of the function and of the line (see below).
If the slope is [math]\displaystyle{ a=0 }[/math], this is a constant function [math]\displaystyle{ f(x)=b }[/math] defining a horizontal line, which some authors exclude from the class of linear functions.[3] With this definition, the degree of a linear polynomial would be exactly one, and its graph would be a line that is neither vertical nor horizontal. However, in this article, [math]\displaystyle{ a\neq 0 }[/math] is required, so constant functions will be considered linear.
If [math]\displaystyle{ b=0 }[/math] then the linear function is said to be homogeneous. Such function defines a line that passes through the origin of the coordinate system, that is, the point [math]\displaystyle{ (x,y)=(0,0) }[/math]. In advanced mathematics texts, the term linear function often denotes specifically homogeneous linear functions, while the term affine function is used for the general case, which includes [math]\displaystyle{ b\neq0 }[/math].
The natural domain of a linear function [math]\displaystyle{ f(x) }[/math], the set of allowed input values for x, is the entire set of real numbers, [math]\displaystyle{ x\in \mathbb R. }[/math] One can also consider such functions with x in an arbitrary field, taking the coefficients a, b in that field.
The graph [math]\displaystyle{ y=f(x)=ax+b }[/math] is a non-vertical line having exactly one intersection with the y-axis, its y-intercept point [math]\displaystyle{ (x,y)=(0,b). }[/math] The y-intercept value [math]\displaystyle{ y=f(0)=b }[/math] is also called the initial value of [math]\displaystyle{ f(x). }[/math] If [math]\displaystyle{ a\neq 0, }[/math] the graph is a non-horizontal line having exactly one intersection with the x-axis, the x-intercept point [math]\displaystyle{ (x,y)=(-\tfrac ba,0). }[/math] The x-intercept value [math]\displaystyle{ x=-\tfrac ba, }[/math] the solution of the equation [math]\displaystyle{ f(x)=0, }[/math] is also called the root or zero of [math]\displaystyle{ f(x). }[/math]
Slope
The slope of a nonvertical line is a number that measures how steeply the line is slanted (rise-over-run). If the line is the graph of the linear function [math]\displaystyle{ f(x) = ax + b }[/math], this slope is given by the constant a.
The slope measures the constant rate of change of [math]\displaystyle{ f(x) }[/math] per unit change in x: whenever the input x is increased by one unit, the output changes by a units: [math]\displaystyle{ f(x{+}1)=f(x)+a }[/math], and more generally [math]\displaystyle{ f(x{+}\Delta x)=f(x)+a\Delta x }[/math] for any number [math]\displaystyle{ \Delta x }[/math]. If the slope is positive, [math]\displaystyle{ a \gt 0 }[/math], then the function [math]\displaystyle{ f(x) }[/math] is increasing; if [math]\displaystyle{ a \lt 0 }[/math], then [math]\displaystyle{ f(x) }[/math] is decreasing
In calculus, the derivative of a general function measures its rate of change. A linear function [math]\displaystyle{ f(x)=ax+b }[/math] has a constant rate of change equal to its slope a, so its derivative is the constant function [math]\displaystyle{ f\,'(x)=a }[/math].
The fundamental idea of differential calculus is that any smooth function [math]\displaystyle{ f(x) }[/math] (not necessarily linear) can be closely approximated near a given point [math]\displaystyle{ x=c }[/math] by a unique linear function. The derivative [math]\displaystyle{ f\,'(c) }[/math] is the slope of this linear function, and the approximation is: [math]\displaystyle{ f(x) \approx f\,'(c)(x{-}c)+f(c) }[/math] for [math]\displaystyle{ x\approx c }[/math]. The graph of the linear approximation is the tangent line of the graph [math]\displaystyle{ y=f(x) }[/math] at the point [math]\displaystyle{ (c,f(c)) }[/math]. The derivative slope [math]\displaystyle{ f\,'(c) }[/math] generally varies with the point c. Linear functions can be characterized as the only real functions whose derivative is constant: if [math]\displaystyle{ f\,'(x)=a }[/math] for all x, then [math]\displaystyle{ f(x)=ax+b }[/math] for [math]\displaystyle{ b=f(0) }[/math].
Slope-intercept, point-slope, and two-point forms
A given linear function [math]\displaystyle{ f(x) }[/math] can be written in several standard formulas displaying its various properties. The simplest is the slope-intercept form:
- [math]\displaystyle{ f(x)= ax+b }[/math],
from which one can immediately see the slope a and the initial value [math]\displaystyle{ f(0)=b }[/math], which is the y-intercept of the graph [math]\displaystyle{ y=f(x) }[/math].
Given a slope a and one known value [math]\displaystyle{ f(x_0)=y_0 }[/math], we write the point-slope form:
- [math]\displaystyle{ f(x) = a(x{-}x_0)+y_0 }[/math].
In graphical terms, this gives the line [math]\displaystyle{ y=f(x) }[/math] with slope a passing through the point [math]\displaystyle{ (x_0,y_0) }[/math].
The two-point form starts with two known values [math]\displaystyle{ f(x_0)=y_0 }[/math] and [math]\displaystyle{ f(x_1)=y_1 }[/math]. One computes the slope [math]\displaystyle{ a=\tfrac{y_1-y_0}{x_1-x_0} }[/math] and inserts this into the point-slope form:
- [math]\displaystyle{ f(x) = \tfrac{y_1-y_0}{x_1-x_0}(x{-}x_0\!) + y_0 }[/math].
Its graph [math]\displaystyle{ y=f(x) }[/math] is the unique line passing through the points [math]\displaystyle{ (x_0,y_0\!), (x_1,y_1\!) }[/math]. The equation [math]\displaystyle{ y=f(x) }[/math] may also be written to emphasize the constant slope:
- [math]\displaystyle{ \frac{y-y_0}{x-x_0}=\frac{y_1-y_0}{x_1-x_0} }[/math].
Relationship with linear equations
Linear functions commonly arise from practical problems involving variables [math]\displaystyle{ x,y }[/math] with a linear relationship, that is, obeying a linear equation [math]\displaystyle{ Ax+By=C }[/math]. If [math]\displaystyle{ B\neq 0 }[/math], one can solve this equation for y, obtaining
- [math]\displaystyle{ y = -\tfrac{A}{B}x +\tfrac{C}{B}=ax+b, }[/math]
where we denote [math]\displaystyle{ a=-\tfrac{A}{B} }[/math] and [math]\displaystyle{ b=\tfrac{C}{B} }[/math]. That is, one may consider y as a dependent variable (output) obtained from the independent variable (input) x via a linear function: [math]\displaystyle{ y = f(x) = ax+b }[/math]. In the xy-coordinate plane, the possible values of [math]\displaystyle{ (x,y) }[/math] form a line, the graph of the function [math]\displaystyle{ f(x) }[/math]. If [math]\displaystyle{ B=0 }[/math] in the original equation, the resulting line [math]\displaystyle{ x=\tfrac{C}{A} }[/math] is vertical, and cannot be written as [math]\displaystyle{ y=f(x) }[/math].
The features of the graph [math]\displaystyle{ y = f(x) = ax+b }[/math] can be interpreted in terms of the variables x and y. The y-intercept is the initial value [math]\displaystyle{ y=f(0)=b }[/math] at [math]\displaystyle{ x=0 }[/math]. The slope a measures the rate of change of the output y per unit change in the input x. In the graph, moving one unit to the right (increasing x by 1) moves the y-value up by a: that is, [math]\displaystyle{ f(x{+}1) = f(x) + a }[/math]. Negative slope a indicates a decrease in y for each increase in x.
For example, the linear function [math]\displaystyle{ y = -2x + 4 }[/math] has slope [math]\displaystyle{ a=-2 }[/math], y-intercept point [math]\displaystyle{ (0,b)=(0,4) }[/math], and x-intercept point [math]\displaystyle{ (2,0) }[/math].
Example
Suppose salami and sausage cost €6 and €3 per kilogram, and we wish to buy €12 worth. How much of each can we purchase? If x kilograms of salami and y kilograms of sausage costs a total of €12 then, €6×x + €3×y = €12. Solving for y gives the point-slope form [math]\displaystyle{ y = -2x + 4 }[/math], as above. That is, if we first choose the amount of salami x, the amount of sausage can be computed as a function [math]\displaystyle{ y = f(x) = -2x + 4 }[/math]. Since salami costs twice as much as sausage, adding one kilo of salami decreases the sausage by 2 kilos: [math]\displaystyle{ f(x{+}1) = f(x) - 2 }[/math], and the slope is −2. The y-intercept point [math]\displaystyle{ (x,y)=(0,4) }[/math] corresponds to buying only 4 kg of sausage; while the x-intercept point [math]\displaystyle{ (x,y)=(2,0) }[/math] corresponds to buying only 2 kg of salami.
Note that the graph includes points with negative values of x or y, which have no meaning in terms of the original variables (unless we imagine selling meat to the butcher). Thus we should restrict our function [math]\displaystyle{ f(x) }[/math] to the domain [math]\displaystyle{ 0\le x\le 2 }[/math].
Also, we could choose y as the independent variable, and compute x by the inverse linear function: [math]\displaystyle{ x = g(y) = -\tfrac12 y +2 }[/math] over the domain [math]\displaystyle{ 0\le y \le 4 }[/math].
Relationship with other classes of functions
If the coefficient of the variable is not zero (a ≠ 0), then a linear function is represented by a degree 1 polynomial (also called a linear polynomial), otherwise it is a constant function – also a polynomial function, but of zero degree.
A straight line, when drawn in a different kind of coordinate system may represent other functions.
For example, it may represent an exponential function when its values are expressed in the logarithmic scale. It means that when log(g(x)) is a linear function of x, the function g is exponential. With linear functions, increasing the input by one unit causes the output to increase by a fixed amount, which is the slope of the graph of the function. With exponential functions, increasing the input by one unit causes the output to increase by a fixed multiple, which is known as the base of the exponential function.
If both arguments and values of a function are in the logarithmic scale (i.e., when log(y) is a linear function of log(x)), then the straight line represents a power law:
- [math]\displaystyle{ \log_r y = a \log_r x + b \quad\Rightarrow\quad y = r^b\cdot x^a }[/math]
On the other hand, the graph of a linear function in terms of polar coordinates:
- [math]\displaystyle{ r =f(\theta ) = a\theta + b }[/math]
is an Archimedean spiral if [math]\displaystyle{ a \neq 0 }[/math] and a circle otherwise.
See also
- Affine map, a generalization
- Arithmetic progression, a linear function of integer argument
Notes
- ↑ Stewart 2012, p. 23
- ↑ Stewart 2012, p. 24
- ↑ Swokowski 1983, p. 34
References
- James Stewart (2012), Calculus: Early Transcendentals, edition 7E, Brooks/Cole. ISBN 978-0-538-49790-9
- Swokowski, Earl W. (1983), Calculus with analytic geometry (Alternate ed.), Boston: Prindle, Weber & Schmidt, ISBN 0871503417, https://archive.org/details/calculuswithanal00swok
External links
- https://web.archive.org/web/20130524101825/http://www.math.okstate.edu/~noell/ebsm/linear.html
- https://web.archive.org/web/20180722042342/https://corestandards.org/assets/CCSSI_Math%20Standards.pdf
 |