Left-child right-sibling binary tree
Every multi-way or k-ary tree structure studied in computer science admits a representation as a binary tree, which goes by various names including child-sibling representation,[1] left-child, right-sibling binary tree,[2] doubly chained tree or filial-heir chain.[3]
In a binary tree that represents a multi-way tree T, each node corresponds to a node in T and has two pointers: one to the node's first child, and one to its next sibling in T. The children of a node thus form a singly-linked list. To find a node n's k'th child, one needs to traverse this list:
procedure kth-child(n, k):
child ← n.child
while k ≠ 0 and child ≠ nil:
child ← child.next-sibling
k ← k − 1
return child // may return nil
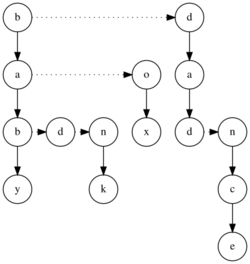
The process of converting from a k-ary tree to an LC-RS binary tree is sometimes called the Knuth transform.[4] To form a binary tree from an arbitrary k-ary tree by this method, the root of the original tree is made the root of the binary tree. Then, starting with the root, each node's leftmost child in the original tree is made its left child in the binary tree, and its nearest sibling to the right in the original tree is made its right child in the binary tree.
Doubly chained trees were described by Edward H. Sussenguth in 1963.[5]
Processing a k-ary tree to LC-RS binary tree, every node is linked and aligned with the left child, and the next nearest is a sibling. For example, we have a ternary tree below:
1
/|\
/ | \
/ | \
2 3 4
/ \ |
5 6 7
/ \
8 9
We can re-write it by putting the left child node to one level below its parents and by putting the sibling next to the child at the same level – it will be linear (same line).
1
/
/
/
2---3---4
/ /
5---6 7
/
8---9
We can transform this tree to a binary tree by turning each sibling 45° clockwise.[6]
1
/
2
/ \
5 3
\ \
6 4
/
7
/
8
\
9
Use cases
The LCRS representation is more space-efficient than a traditional multiway tree, but comes at the cost that looking up a node's children by index becomes slower. Therefore, the LCRS representation is preferable if
- Memory efficiency is a concern, and/or
- Random access of a node's children is not required.
Case (1) applies when large multi-way trees are necessary, especially when the trees contains a large set of data. For example, if storing a phylogenetic tree, the LCRS representation might be suitable.
Case (2) arises in specialized data structures in which the tree structure is being used in very specific ways. For example, many types of heap data structures that use multi-way trees can be space optimized by using the LCRS representation. (Examples include Fibonacci heaps, pairing heaps and weak heaps.) The main reason for this is that in heap data structures, the most common operations tend to be
- Remove the root of a tree and process each of its children, or
- Join two trees together by making one tree a child of the other.
Operation (1) it is very efficient. In LCRS representation, it organizes the tree to have a right child because it does not have a sibling, so it is easy to remove the root.
Operation (2) it is also efficient. It is easy to join two trees together.[7]
References
- ↑ Fredman, Michael L.; Sedgewick, Robert; Sleator, Daniel D.; Tarjan, Robert E. (1986). "The pairing heap: a new form of self-adjusting heap". Algorithmica 1 (1): 111–129. doi:10.1007/BF01840439. https://www.cs.cmu.edu/~sleator/papers/pairing-heaps.pdf.
- ↑ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 214–217. ISBN 0-262-03293-7.
- ↑
This article incorporates public domain material from the NIST document: Black, Paul E.. "Binary tree representation of trees". https://xlinux.nist.gov/dads/HTML/binaryTreeRepofTree.html.
- ↑ Computer Data Structures. John L. Pfaltz.
- ↑ Sussenguth, Edward H. (May 1963). "Use of tree structures for processing files". Communications of the ACM 6 (5): 272–279. doi:10.1145/366552.366600.
- ↑ "binary tree representation of trees". https://xlinux.nist.gov/dads/HTML/binaryTreeRepofTree.html. Retrieved 2015-11-24.
- ↑ "What is the left-child, right-sibling representation of a tree? Why would you use it?". https://stackoverflow.com/questions/14015525/what-is-the-left-child-right-sibling-representation-of-a-tree-why-would-you-u. Retrieved 2016-12-12.
 |  |
