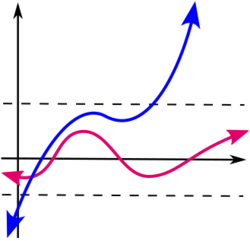
Bounded function
In mathematics, a function [math]\displaystyle{ f }[/math] defined on some set [math]\displaystyle{ X }[/math] with real or complex values is called bounded if the set of its values is bounded. In other words, there exists a real number [math]\displaystyle{ M }[/math] such that
- [math]\displaystyle{ |f(x)|\le M }[/math]
for all [math]\displaystyle{ x }[/math] in [math]\displaystyle{ X }[/math].[1] A function that is not bounded is said to be unbounded.[citation needed]
If [math]\displaystyle{ f }[/math] is real-valued and [math]\displaystyle{ f(x) \leq A }[/math] for all [math]\displaystyle{ x }[/math] in [math]\displaystyle{ X }[/math], then the function is said to be bounded (from) above by [math]\displaystyle{ A }[/math]. If [math]\displaystyle{ f(x) \geq B }[/math] for all [math]\displaystyle{ x }[/math] in [math]\displaystyle{ X }[/math], then the function is said to be bounded (from) below by [math]\displaystyle{ B }[/math]. A real-valued function is bounded if and only if it is bounded from above and below.[1][additional citation(s) needed]
An important special case is a bounded sequence, where [math]\displaystyle{ X }[/math] is taken to be the set [math]\displaystyle{ \mathbb N }[/math] of natural numbers. Thus a sequence [math]\displaystyle{ f = (a_0, a_1, a_2, \ldots) }[/math] is bounded if there exists a real number [math]\displaystyle{ M }[/math] such that
- [math]\displaystyle{ |a_n|\le M }[/math]
for every natural number [math]\displaystyle{ n }[/math]. The set of all bounded sequences forms the sequence space [math]\displaystyle{ l^\infty }[/math].[citation needed]
The definition of boundedness can be generalized to functions [math]\displaystyle{ f: X \rightarrow Y }[/math] taking values in a more general space [math]\displaystyle{ Y }[/math] by requiring that the image [math]\displaystyle{ f(X) }[/math] is a bounded set in [math]\displaystyle{ Y }[/math].[citation needed]
Related notions
Weaker than boundedness is local boundedness. A family of bounded functions may be uniformly bounded.
A bounded operator [math]\displaystyle{ T: X \rightarrow Y }[/math] is not a bounded function in the sense of this page's definition (unless [math]\displaystyle{ T=0 }[/math]), but has the weaker property of preserving boundedness; bounded sets [math]\displaystyle{ M \subseteq X }[/math] are mapped to bounded sets [math]\displaystyle{ T(M) \subseteq Y }[/math]. This definition can be extended to any function [math]\displaystyle{ f: X \rightarrow Y }[/math] if [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] allow for the concept of a bounded set. Boundedness can also be determined by looking at a graph.[citation needed]
Examples
- The sine function [math]\displaystyle{ \sin: \mathbb R \rightarrow \mathbb R }[/math] is bounded since [math]\displaystyle{ |\sin (x)| \le 1 }[/math] for all [math]\displaystyle{ x \in \mathbb{R} }[/math].[1][2]
- The function [math]\displaystyle{ f(x)=(x^2-1)^{-1} }[/math], defined for all real [math]\displaystyle{ x }[/math] except for −1 and 1, is unbounded. As [math]\displaystyle{ x }[/math] approaches −1 or 1, the values of this function get larger in magnitude. This function can be made bounded if one restricts its domain to be, for example, [math]\displaystyle{ [2, \infty) }[/math] or [math]\displaystyle{ (-\infty, -2] }[/math].[citation needed]
- The function [math]\displaystyle{ f(x)= (x^2+1)^{-1} }[/math], defined for all real [math]\displaystyle{ x }[/math], is bounded, since [math]\displaystyle{ |f(x)| \le 1 }[/math] for all [math]\displaystyle{ x }[/math].[citation needed]
- The inverse trigonometric function arctangent defined as: [math]\displaystyle{ y= \arctan (x) }[/math] or [math]\displaystyle{ x = \tan (y) }[/math] is increasing for all real numbers [math]\displaystyle{ x }[/math] and bounded with [math]\displaystyle{ -\frac{\pi}{2} \lt y \lt \frac{\pi}{2} }[/math] radians[3]
- By the boundedness theorem, every continuous function on a closed interval, such as [math]\displaystyle{ f: [0, 1] \rightarrow \mathbb R }[/math], is bounded.[4] More generally, any continuous function from a compact space into a metric space is bounded.[citation needed]
- All complex-valued functions [math]\displaystyle{ f: \mathbb C \rightarrow \mathbb C }[/math] which are entire are either unbounded or constant as a consequence of Liouville's theorem.[5] In particular, the complex [math]\displaystyle{ \sin: \mathbb C \rightarrow \mathbb C }[/math] must be unbounded since it is entire.[citation needed]
- The function [math]\displaystyle{ f }[/math] which takes the value 0 for [math]\displaystyle{ x }[/math] rational number and 1 for [math]\displaystyle{ x }[/math] irrational number (cf. Dirichlet function) is bounded. Thus, a function does not need to be "nice" in order to be bounded. The set of all bounded functions defined on [math]\displaystyle{ [0, 1] }[/math] is much larger than the set of continuous functions on that interval.[citation needed] Moreover, continuous functions need not be bounded; for example, the functions [math]\displaystyle{ g:\mathbb{R}^2\to\mathbb{R} }[/math] and [math]\displaystyle{ h: (0, 1)^2\to\mathbb{R} }[/math] defined by [math]\displaystyle{ g(x, y) := x + y }[/math] and [math]\displaystyle{ h(x, y) := \frac{1}{x+y} }[/math] are both continuous, but neither is bounded.[6] (However, a continuous function must be bounded if its domain is both closed and bounded.[6])
See also
References
- ↑ 1.0 1.1 1.2 Jeffrey, Alan (1996-06-13) (in en). Mathematics for Engineers and Scientists, 5th Edition. CRC Press. ISBN 978-0-412-62150-5. https://books.google.com/books?id=jMUbUCUOaeQC&dq=%22Bounded+function%22&pg=PA66.
- ↑ "The Sine and Cosine Functions". https://math.dartmouth.edu/opencalc2/cole/lecture10.pdf.
- ↑ Polyanin, Andrei D.; Chernoutsan, Alexei (2010-10-18) (in en). A Concise Handbook of Mathematics, Physics, and Engineering Sciences. CRC Press. ISBN 978-1-4398-0640-1. https://books.google.com/books?id=ejzScufwDRUC&dq=arctangent+bounded&pg=PA27.
- ↑ Weisstein, Eric W.. "Extreme Value Theorem" (in en). https://mathworld.wolfram.com/ExtremeValueTheorem.html.
- ↑ "Liouville theorems - Encyclopedia of Mathematics". https://encyclopediaofmath.org/wiki/Liouville_theorems.
- ↑ 6.0 6.1 Ghorpade, Sudhir R.; Limaye, Balmohan V. (2010-03-20) (in en). A Course in Multivariable Calculus and Analysis. Springer Science & Business Media. pp. 56. ISBN 978-1-4419-1621-1. https://books.google.com/books?id=JVFJAAAAQBAJ&q=%22Bounded+function%22.
 |