Sign function
In mathematics, the sign function or signum function (from signum, Latin for "sign") is a function that returns the sign of a real number. In mathematical notation the sign function is often represented as [math]\displaystyle{ \sgn (x) }[/math].[1]
Definition
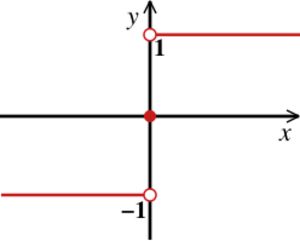
The signum function of a real number [math]\displaystyle{ x }[/math] is a piecewise function which is defined as follows:[1] [math]\displaystyle{ \sgn x :=\begin{cases} -1 & \text{if } x \lt 0, \\ 0 & \text{if } x = 0, \\ 1 & \text{if } x \gt 0. \end{cases} }[/math]
Properties
Any real number can be expressed as the product of its absolute value and its sign function: [math]\displaystyle{ x = |x| \sgn x. }[/math]
It follows that whenever [math]\displaystyle{ x }[/math] is not equal to 0 we have [math]\displaystyle{ \sgn x = \frac{x}{|x|} = \frac{|x|}{x}\,. }[/math]
Similarly, for any real number [math]\displaystyle{ x }[/math], [math]\displaystyle{ |x| = x\sgn x. }[/math] We can also ascertain that: [math]\displaystyle{ \sgn x^n=(\sgn x)^n. }[/math] The signum function is the derivative of the absolute value function, up to (but not including) the indeterminacy at zero. More formally, in integration theory it is a weak derivative, and in convex function theory the subdifferential of the absolute value at 0 is the interval [math]\displaystyle{ [-1,1] }[/math], "filling in" the sign function (the subdifferential of the absolute value is not single-valued at 0). Note, the resultant power of [math]\displaystyle{ x }[/math] is 0, similar to the ordinary derivative of [math]\displaystyle{ x }[/math]. The numbers cancel and all we are left with is the sign of [math]\displaystyle{ x }[/math]. [math]\displaystyle{ \frac{\text{d} |x|}{\text{d}x} = \sgn x \text{ for } x \ne 0\,. }[/math]
The signum function is differentiable with derivative 0 everywhere except at 0. It is not differentiable at 0 in the ordinary sense, but under the generalised notion of differentiation in distribution theory, the derivative of the signum function is two times the Dirac delta function, which can be demonstrated using the identity [2] [math]\displaystyle{ \sgn x = 2 H(x) - 1 \,, }[/math] where [math]\displaystyle{ H(x) }[/math] is the Heaviside step function using the standard [math]\displaystyle{ H(0)=\frac{1}{2} }[/math] formalism. Using this identity, it is easy to derive the distributional derivative:[3] [math]\displaystyle{ \frac{\text{d}\sgn x}{\text{d}x} = 2 \frac{\text{d} H(x)}{\text{d}x} = 2\delta(x) \,. }[/math]
The Fourier transform of the signum function is[4] [math]\displaystyle{ \int_{-\infty}^\infty (\sgn x) e^{-ikx}\text{d}x = PV\frac{2}{ik}, }[/math] where [math]\displaystyle{ PV }[/math] means taking the Cauchy principal value.
The signum can also be written using the Iverson bracket notation: [math]\displaystyle{ \sgn x = -[x \lt 0] + [x \gt 0] \,. }[/math]
The signum can also be written using the floor and the absolute value functions: [math]\displaystyle{ \sgn x = \Biggl\lfloor \frac{x}{|x|+1} \Biggr\rfloor - \Biggl\lfloor \frac{-x}{|x|+1} \Biggr\rfloor \,. }[/math]The signum function has a very simple definition if [math]\displaystyle{ 0^0 }[/math] is accepted to be equal to 1. Then signum can be written for all real numbers as [math]\displaystyle{ \sgn x = 0^ \left ( - x + \left\vert x \right\vert \right ) - 0^ \left ( x + \left\vert x \right\vert \right ) \,. }[/math] The signum function coincides with the limits [math]\displaystyle{ \sgn x=\lim_{n\to\infty}\frac{1-2^{-nx}}{1+2^{-nx}}\,. }[/math] and [math]\displaystyle{ \sgn x = \lim_{n\to\infty}\frac{2}{\pi}{\rm arctan}(nx)\, = \lim_{n\to\infty}\frac{2}{\pi}\tan^{-1}(nx)\,. }[/math]as well as,
[math]\displaystyle{ \sgn x=\lim_{n\to\infty}\tanh(nx)\,. }[/math]Here, [math]\displaystyle{ \tanh(x) }[/math] is the Hyperbolic tangent and the superscript of -1, above it, is shorthand notation for the inverse function of the Trigonometric function, tangent.
For [math]\displaystyle{ k\gt 1 }[/math], a smooth approximation of the sign function is [math]\displaystyle{ \sgn x \approx \tanh kx \,. }[/math] Another approximation is [math]\displaystyle{ \sgn x \approx \frac{x}{\sqrt{x^2 + \varepsilon^2}} \,. }[/math] which gets sharper as [math]\displaystyle{ \varepsilon\to 0 }[/math]; note that this is the derivative of [math]\displaystyle{ \sqrt{x^2+\varepsilon ^2} }[/math]. This is inspired from the fact that the above is exactly equal for all nonzero [math]\displaystyle{ x }[/math] if [math]\displaystyle{ \varepsilon=0 }[/math], and has the advantage of simple generalization to higher-dimensional analogues of the sign function (for example, the partial derivatives of [math]\displaystyle{ \sqrt{x^2+y^2} }[/math]).
See Heaviside step function § Analytic approximations.
Complex signum
The signum function can be generalized to complex numbers as: [math]\displaystyle{ \sgn z = \frac{z}{|z|} }[/math] for any complex number [math]\displaystyle{ z }[/math] except [math]\displaystyle{ z=0 }[/math]. The signum of a given complex number [math]\displaystyle{ z }[/math] is the point on the unit circle of the complex plane that is nearest to [math]\displaystyle{ z }[/math]. Then, for [math]\displaystyle{ z\ne 0 }[/math], [math]\displaystyle{ \sgn z = e^{i\arg z}\,, }[/math] where [math]\displaystyle{ \arg }[/math] is the complex argument function.
For reasons of symmetry, and to keep this a proper generalization of the signum function on the reals, also in the complex domain one usually defines, for [math]\displaystyle{ z=0 }[/math]: [math]\displaystyle{ \sgn(0+0i)=0 }[/math]
Another generalization of the sign function for real and complex expressions is [math]\displaystyle{ \text{csgn} }[/math],[5] which is defined as: [math]\displaystyle{ \operatorname{csgn} z= \begin{cases} 1 & \text{if } \mathrm{Re}(z) \gt 0, \\ -1 & \text{if } \mathrm{Re}(z) \lt 0, \\ \sgn \mathrm{Im}(z) & \text{if } \mathrm{Re}(z) = 0 \end{cases} }[/math] where [math]\displaystyle{ \text{Re}(z) }[/math] is the real part of [math]\displaystyle{ z }[/math] and [math]\displaystyle{ \text{Im}(z) }[/math] is the imaginary part of [math]\displaystyle{ z }[/math].
We then have (for [math]\displaystyle{ z\ne 0 }[/math]): [math]\displaystyle{ \operatorname{csgn} z = \frac{z}{\sqrt{z^2}} = \frac{\sqrt{z^2}}{z}. }[/math]
Generalized signum function
At real values of [math]\displaystyle{ x }[/math], it is possible to define a generalized function–version of the signum function, [math]\displaystyle{ \varepsilon (x) }[/math] such that [math]\displaystyle{ \varepsilon (x)^2=1 }[/math] everywhere, including at the point [math]\displaystyle{ x=0 }[/math], unlike [math]\displaystyle{ \sgn }[/math], for which [math]\displaystyle{ (\sgn 0)^2=0 }[/math]. This generalized signum allows construction of the algebra of generalized functions, but the price of such generalization is the loss of commutativity. In particular, the generalized signum anticommutes with the Dirac delta function[6] [math]\displaystyle{ \varepsilon (x) \delta(x)+\delta(x) \varepsilon(x) = 0 \, ; }[/math] in addition, [math]\displaystyle{ \varepsilon (x) }[/math] cannot be evaluated at [math]\displaystyle{ x=0 }[/math]; and the special name, [math]\displaystyle{ \varepsilon }[/math] is necessary to distinguish it from the function [math]\displaystyle{ \sgn }[/math]. ([math]\displaystyle{ \varepsilon (0) }[/math] is not defined, but [math]\displaystyle{ \sgn 0=0 }[/math].)
Generalization to matrices
Thanks to the Polar decomposition theorem, a matrix [math]\displaystyle{ \boldsymbol A\in\mathbb K^{n\times n} }[/math] ([math]\displaystyle{ n\in\mathbb N }[/math] and [math]\displaystyle{ \mathbb K\in\{\mathbb R,\mathbb C\} }[/math]) can be decomposed as a product [math]\displaystyle{ \boldsymbol Q\boldsymbol P }[/math] where [math]\displaystyle{ \boldsymbol Q }[/math] is a unitary matrix and [math]\displaystyle{ \boldsymbol P }[/math] is a self-adjoint, or Hermitian, positive definite matrix, both in [math]\displaystyle{ \mathbb K^{n\times n} }[/math]. If [math]\displaystyle{ \boldsymbol A }[/math] is invertible then such a decomposition is unique and [math]\displaystyle{ \boldsymbol Q }[/math] plays the role of [math]\displaystyle{ \boldsymbol A }[/math]'s signum. A dual construction is given by the decomposition [math]\displaystyle{ \boldsymbol A=\boldsymbol S\boldsymbol R }[/math] where [math]\displaystyle{ \boldsymbol R }[/math] is unitary, but generally different than [math]\displaystyle{ \boldsymbol Q }[/math]. This leads to each invertible matrix having a unique left-signum [math]\displaystyle{ \boldsymbol Q }[/math] and right-signum [math]\displaystyle{ \boldsymbol R }[/math].
In the special case where [math]\displaystyle{ \mathbb K=\mathbb R,\ n=2, }[/math] and the (invertible) matrix [math]\displaystyle{ \boldsymbol A = \left[\begin{array}{rr}a&-b\\b&a\end{array}\right] }[/math], which identifies with the (nonzero) complex number [math]\displaystyle{ a+\mathrm i b=c }[/math], then the signum matrices satisfy [math]\displaystyle{ \boldsymbol Q=\boldsymbol P=\left[\begin{array}{rr}a&-b\\b&a\end{array}\right]/|c| }[/math] and identify with the complex signum of [math]\displaystyle{ c }[/math], [math]\displaystyle{ \sgn c = c/|c| }[/math]. In this sense, polar decomposition generalizes to matrices the signum-modulus decomposition of complex numbers.
See also
- Absolute value
- Heaviside function
- Negative number
- Rectangular function
- Sigmoid function (Hard sigmoid)
- Step function (Piecewise constant function)
- Three-way comparison
- Zero crossing
- Polar decomposition
Notes
- ↑ 1.0 1.1 "Signum function - Maeckes". http://www.maeckes.nl/Signum%20functie%20GB.html.
- ↑ Weisstein, Eric W.. "Sign". http://mathworld.wolfram.com/Sign.html.
- ↑ Weisstein, Eric W.. "Heaviside Step Function". http://mathworld.wolfram.com/HeavisideStepFunction.html.
- ↑ Burrows, B. L.; Colwell, D. J. (1990). "The Fourier transform of the unit step function". International Journal of Mathematical Education in Science and Technology 21 (4): 629–635. doi:10.1080/0020739900210418.
- ↑ Maple V documentation. May 21, 1998
- ↑ Yu.M.Shirokov (1979). "Algebra of one-dimensional generalized functions". Theoretical and Mathematical Physics 39 (3): 471–477. doi:10.1007/BF01017992. http://springerlink.metapress.com/content/w3010821x8267824/?p=5bb23f98d846495c808e0a2e642b983a&pi=3.
 |