Birthday problem

Short description: Mathematical problem

For yearly variation in mortality rates, see Birthday effect. For the mathematical brain teaser that was asked in the Math Olympiad, see Cheryl's Birthday.

The computed probability of at least two people sharing a birthday versus the number of people

In probability theory, the birthday problem asks for the probability that, in a set of n randomly chosen people, at least two will share a birthday. The birthday paradox refers to the counterintuitive fact that only 23 people are needed for that probability to exceed 50%.

The birthday paradox is a veridical paradox: it seems wrong at first glance but is, in fact, true. While it may seem surprising that only 23 individuals are required to reach a 50% probability of a shared birthday, this result is made more intuitive by considering that the birthday comparisons will be made between every possible pair of individuals. With 23 individuals, there are 23 × 22/2 = 253 pairs to consider, far more than half the number of days in a year.

Real-world applications for the birthday problem include a cryptographic attack called the birthday attack, which uses this probabilistic model to reduce the complexity of finding a collision for a hash function, as well as calculating the approximate risk of a hash collision existing within the hashes of a given size of population.

The problem is generally attributed to Harold Davenport in about 1927, though he did not publish it at the time. Davenport did not claim to be its discoverer "because he could not believe that it had not been stated earlier". The first publication of a version of the birthday problem was by Richard von Mises in 1939.

Calculating the probability

From a permutations perspective, let the event A be the probability of finding a group of 23 people without any repeated birthdays. Where the event B is the probability of finding a group of 23 people with at least two people sharing same birthday, P(B) = 1 − P(A). P(A) is the ratio of the total number of birthdays, [math]\displaystyle{ V_{nr} }[/math], without repetitions and order matters (e.g. for a group of 2 people, mm/dd birthday format, one possible outcome is [math]\displaystyle{ \left \{ \left \{01/02,05/20\right \},\left \{05/20,01/02\right \},\left \{10/02,08/04\right\},...\right \} }[/math]) divided by the total number of birthdays with repetition and order matters, [math]\displaystyle{ V_{t} }[/math], as it is the total space of outcomes from the experiment (e.g. 2 people, one possible outcome is [math]\displaystyle{ \left \{ \left \{01/02,01/02\right \},\left \{10/02,08/04\right \},...\right \} }[/math]). Therefore [math]\displaystyle{ V_{nr} }[/math] and [math]\displaystyle{ V_{t} }[/math] are permutations.

[math]\displaystyle{ \begin{align} V_{nr} &= \frac{n!}{(n-k)!} = \frac{365!}{(365-23)!} \\[8pt] V_t &= n^k = 365^{23} \\[8pt] P(A) &= \frac{V_{nr}}{V_t} \approx 0.492703 \\[8pt] P(B) &= 1 - P(A) \approx 1 - 0.492703 \approx 0.507297 \quad (50.7297\%)\end{align} }[/math]

Another way the birthday problem can be solved is by asking for an approximate probability that in a group of n people at least two have the same birthday. For simplicity, leap years, twins, selection bias, and seasonal and weekly variations in birth rates are generally disregarded, and instead it is assumed that there are 365 possible birthdays, and that each person's birthday is equally likely to be any of these days, independent of the other people in the group. For independent birthdays, the uniform distribution on birthdays is the distribution that minimizes the probability of two people with the same birthday; any unevenness increases this probability. The problem of a non-uniform number of births occurring during each day of the year was first addressed by Murray Klamkin in 1967. As it happens, the real-world distribution yields a critical size of 23 to reach 50%.

The goal is to compute P(B), the probability that at least two people in the room have the same birthday. However, it is simpler to calculate P(A′), the probability that no two people in the room have the same birthday. Then, because B and A′ are the only two possibilities and are also mutually exclusive, P(B) = 1 − P(A′).

Here is the calculation of P(B) for 23 people. Let the 23 people be numbered 1 to 23. The event that all 23 people have different birthdays is the same as the event that person 2 does not have the same birthday as person 1, and that person 3 does not have the same birthday as either person 1 or person 2, and so on, and finally that person 23 does not have the same birthday as any of persons 1 through 22. Let these events be called Event 2, Event 3, and so on. Event 1 is the event of person 1 having a birthday, which occurs with probability 1. This conjunction of events may be computed using conditional probability: the probability of Event 2 is 364/365, as person 2 may have any birthday other than the birthday of person 1. Similarly, the probability of Event 3 given that Event 2 occurred is 363/365, as person 3 may have any of the birthdays not already taken by persons 1 and 2. This continues until finally the probability of Event 23 given that all preceding events occurred is 343/365. Finally, the principle of conditional probability implies that P(A′) is equal to the product of these individual probabilities:

[math]\displaystyle{ P(A')=\frac{365}{365}\times\frac{364}{365}\times\frac{363}{365}\times\frac{362}{365}\times\cdots\times\frac{343}{365} }[/math]

(1)

The terms of equation (1) can be collected to arrive at:

[math]\displaystyle{ P(A')=\left(\frac{1}{365}\right)^{23}\times(365\times364\times363\times\cdots\times343) }[/math]

(2)

Evaluating equation (2) gives P(A′) ≈ 0.492703

Therefore, P(B) ≈ 1 − 0.492703 = 0.507297 (50.7297%).

This process can be generalized to a group of n people, where p(n) is the probability of at least two of the n people sharing a birthday. It is easier to first calculate the probability p(n) that all n birthdays are different. According to the pigeonhole principle, p(n) is zero when n > 365. When n ≤ 365:

[math]\displaystyle{ \begin{align} \bar p(n) &= 1 \times \left(1-\frac{1}{365}\right) \times \left(1-\frac{2}{365}\right) \times \cdots \times \left(1-\frac{n-1}{365}\right) \\[6pt] &= \frac{ 365 \times 364 \times \cdots \times (365-n+1) }{ 365^n } \\[6pt] &= \frac{ 365! }{ 365^n (365-n)!} = \frac{n!\cdot\binom{365}{n}}{365^n} = \frac{_{365}P_n}{365^n}\end{align} }[/math]

where ! is the factorial operator, Template:Pars is the binomial coefficient and _kP_r denotes permutation.

The equation expresses the fact that the first person has no one to share a birthday, the second person cannot have the same birthday as the first Template:Pars, the third cannot have the same birthday as either of the first two Template:Pars, and in general the nth birthday cannot be the same as any of the n − 1 preceding birthdays.

The event of at least two of the n persons having the same birthday is complementary to all n birthdays being different. Therefore, its probability p(n) is

[math]\displaystyle{ p(n) = 1 - \bar p(n). }[/math]

The following table shows the probability for some other values of n (for this table, the existence of leap years is ignored, and each birthday is assumed to be equally likely):

The probability that no two people share a birthday in a group of n people. Note that the vertical scale is logarithmic (each step down is 10²⁰ times less likely).

n	p(n)
1	00.0%
5	02.7%
10	11.7%
20	41.1%
23	50.7%
30	70.6%
40	89.1%
50	97.0%
60	99.4%
70	99.9%
75	99.97%
100	99.99997%
200	99.9999999999999999999999999998%
300	(100 − 6×10−80)%
350	(100 − 3×10−129)%
365	(100 − 1.45×10−155)%
≥ 366	100%

Approximations

Graphs showing the approximate probabilities of at least two people sharing a birthday (red) and its complementary event (blue)

A graph showing the accuracy of the approximation 1 − e^−n2/730 (red)

The Taylor series expansion of the exponential function (the constant e ≈ 2.718281828)

[math]\displaystyle{ e^x = 1 + x + \frac{x^2}{2!}+\cdots }[/math]

provides a first-order approximation for e^x for [math]\displaystyle{ |x| \ll 1 }[/math]:

[math]\displaystyle{ e^x \approx 1 + x. }[/math]

To apply this approximation to the first expression derived for p(n), set x = −a/365. Thus,

[math]\displaystyle{ e^{-a/365} \approx 1 - \frac{a}{365}. }[/math]

Then, replace a with non-negative integers for each term in the formula of p(n) until a = n − 1, for example, when a = 1,

[math]\displaystyle{ e^{-1/365} \approx 1 - \frac{1}{365}. }[/math]

The first expression derived for p(n) can be approximated as

[math]\displaystyle{ \begin{align} \bar p(n) & \approx 1 \cdot e^{-1/365} \cdot e^{-2/365} \cdots e^{-(n-1)/365} \\[6pt] & = e^{-\big(1+2+ \,\cdots\, +(n-1)\big)/365} \\[6pt] & = e^{-\frac{n(n-1)/2}{365}} = e^{-\frac{n(n-1)}{730}}. \end{align} }[/math]

Therefore,

[math]\displaystyle{ p(n) = 1-\bar p(n) \approx 1 - e^{-\frac{n(n-1)}{730}}. }[/math]

An even coarser approximation is given by

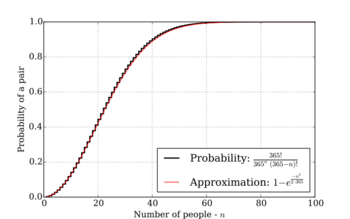
[math]\displaystyle{ p(n)\approx 1-e^{-\frac{n^2}{730}}, }[/math]

which, as the graph illustrates, is still fairly accurate.

According to the approximation, the same approach can be applied to any number of "people" and "days". If rather than 365 days there are d, if there are n persons, and if n ≪ d, then using the same approach as above we achieve the result that if p(n, d) is the probability that at least two out of n people share the same birthday from a set of d available days, then:

[math]\displaystyle{ \begin{align} p(n, d) & \approx 1-e^{-\frac{n(n-1)}{2d}} \\[6pt] & \approx 1-e^{-\frac{n^2}{2d}}. \end{align} }[/math]

Simple exponentiation

The probability of any two people not having the same birthday is 364/365. In a room containing n people, there are Template:Pars = n(n − 1)/2 pairs of people, i.e. Template:Pars events. The probability of no two people sharing the same birthday can be approximated by assuming that these events are independent and hence by multiplying their probability together. Being independent would be equivalent to picking with replacement, any pair of people in the world, not just in a room. In short 364/365 can be multiplied by itself Template:Pars times, which gives us

[math]\displaystyle{ \bar p(n) \approx \left(\frac{364}{365}\right)^\binom{n}{2}. }[/math]

Since this is the probability of no one having the same birthday, then the probability of someone sharing a birthday is

[math]\displaystyle{ p(n) \approx 1 - \left(\frac{364}{365}\right)^\binom{n}{2}. }[/math]

And for the group of 23 people, the probability of sharing is

[math]\displaystyle{ p(23) \approx 1 - \left(\frac{364}{365}\right)^\binom{23}{2} = 1 - \left(\frac{364}{365}\right)^{253} \approx 0.500477 . }[/math]

Poisson approximation

Applying the Poisson approximation for the binomial on the group of 23 people,

[math]\displaystyle{ \operatorname{Poi}\left(\frac{\binom{23}{2}}{365}\right) =\operatorname{Poi}\left(\frac{253}{365}\right) \approx \operatorname{Poi}(0.6932) }[/math]

so

[math]\displaystyle{ \Pr(X\gt 0)=1-\Pr(X=0) \approx 1-e^{-0.6932} \approx 1-0.499998=0.500002. }[/math]

The result is over 50% as previous descriptions. This approximation is the same as the one above based on the Taylor expansion that uses e^x ≈ 1 + x.

Square approximation

A good rule of thumb which can be used for mental calculation is the relation

[math]\displaystyle{ p(n) \approx \frac{n^2}{2m} }[/math]

which can also be written as

[math]\displaystyle{ n \approx \sqrt { 2m \times p(n)} }[/math]

which works well for probabilities less than or equal to 1/2. In these equations, m is the number of days in a year.

For instance, to estimate the number of people required for a 1/2 chance of a shared birthday, we get

[math]\displaystyle{ n \approx \sqrt{ 2 \times 365 \times \tfrac12} = \sqrt{365} \approx 19 }[/math]

Which is not too far from the correct answer of 23.

Approximation of number of people

This can also be approximated using the following formula for the number of people necessary to have at least a 1/2 chance of matching:

[math]\displaystyle{ n \geq \tfrac{1}{2} + \sqrt{\tfrac{1}{4} + 2 \times \ln(2) \times 365} = 22.999943. }[/math]

This is a result of the good approximation that an event with 1/k probability will have a 1/2 chance of occurring at least once if it is repeated k ln 2 times.

Probability table

length of hex string	no. of bits (b)	hash space size (2b)	Number of hashed elements such that probability of at least one hash collision ≥ p
			p = 10−18	p = 10−15	p = 10−12	p = 10−9	p = 10−6	p = 0.001	p = 0.01	p = 0.25	p = 0.50	p = 0.75
8	32	4.3×109	2	2	2	2.9	93	2.9×103	9.3×103	5.0×104	7.7×104	1.1×105
(10)	(40)	(1.1×1012)	2	2	2	47	1.5×103	4.7×104	1.5×105	8.0×105	1.2×106	1.7×106
(12)	(48)	(2.8×1014)	2	2	24	7.5×102	2.4×104	7.5×105	2.4×106	1.3×107	2.0×107	2.8×107
16	64	1.8×1019	6.1	1.9×102	6.1×103	1.9×105	6.1×106	1.9×108	6.1×108	3.3×109	5.1×109	7.2×109
(24)	(96)	(7.9×1028)	4.0×105	1.3×107	4.0×108	1.3×1010	4.0×1011	1.3×1013	4.0×1013	2.1×1014	3.3×1014	4.7×1014
32	128	3.4×1038	2.6×1010	8.2×1011	2.6×1013	8.2×1014	2.6×1016	8.3×1017	2.6×1018	1.4×1019	2.2×1019	3.1×1019
(48)	(192)	(6.3×1057)	1.1×1020	3.5×1021	1.1×1023	3.5×1024	1.1×1026	3.5×1027	1.1×1028	6.0×1028	9.3×1028	1.3×1029
64	256	1.2×1077	4.8×1029	1.5×1031	4.8×1032	1.5×1034	4.8×1035	1.5×1037	4.8×1037	2.6×1038	4.0×1038	5.7×1038
(96)	(384)	(3.9×10115)	8.9×1048	2.8×1050	8.9×1051	2.8×1053	8.9×1054	2.8×1056	8.9×1056	4.8×1057	7.4×1057	1.0×1058
128	512	1.3×10154	1.6×1068	5.2×1069	1.6×1071	5.2×1072	1.6×1074	5.2×1075	1.6×1076	8.8×1076	1.4×1077	1.9×1077

Comparison of the birthday problem (1) and birthday attack (2):Template:Parabreak In (1), collisions are found within one set, in this case, 3 out of 276 pairings of the 24 lunar astronauts.Template:Parabreak In (2), collisions are found between two sets, in this case, 1 out of 256 pairings of only the first bytes of SHA-256 hashes of 16 variants each of benign and harmful contracts.

The lighter fields in this table show the number of hashes needed to achieve the given probability of collision (column) given a hash space of a certain size in bits (row). Using the birthday analogy: the "hash space size" resembles the "available days", the "probability of collision" resembles the "probability of shared birthday", and the "required number of hashed elements" resembles the "required number of people in a group". One could also use this chart to determine the minimum hash size required (given upper bounds on the hashes and probability of error), or the probability of collision (for fixed number of hashes and probability of error).

For comparison, 10⁻¹⁸ to 10⁻¹⁵ is the uncorrectable bit error rate of a typical hard disk. In theory, 128-bit hash functions, such as MD5, should stay within that range until about 8.2×10¹¹ documents, even if its possible outputs are many more.

An upper bound on the probability and a lower bound on the number of people

The argument below is adapted from an argument of Paul Halmos.

As stated above, the probability that no two birthdays coincide is

[math]\displaystyle{ 1-p(n) = \bar p(n) = \prod_{k=1}^{n-1}\left(1-\frac{k}{365}\right) . }[/math]

As in earlier paragraphs, interest lies in the smallest n such that p(n) > 1/2; or equivalently, the smallest n such that p(n) < 1/2.

Using the inequality 1 − x < e^−x in the above expression we replace 1 − k/365 with e^{​−k⁄₃₆₅}. This yields

[math]\displaystyle{ \bar p(n) = \prod_{k=1}^{n-1}\left(1-\frac{k}{365}\right) \lt \prod_{k=1}^{n-1}\left(e^{-\frac{k}{365}}\right) = e^{-\frac{n(n-1)}{730}} . }[/math]

Therefore, the expression above is not only an approximation, but also an upper bound of p(n). The inequality

[math]\displaystyle{ e^{-\frac{n(n-1)}{730}} \lt \frac{1}{2} }[/math]

implies p(n) < 1/2. Solving for n gives

[math]\displaystyle{ n^2-n \gt 730 \ln 2 . }[/math]

Now, 730 ln 2 is approximately 505.997, which is barely below 506, the value of n² − n attained when n = 23. Therefore, 23 people suffice. Incidentally, solving n² − n = 730 ln 2 for n gives the approximate formula of Frank H. Mathis cited above.

This derivation only shows that at most 23 people are needed to ensure a birthday match with even chance; it leaves open the possibility that n is 22 or less could also work.

Generalizations

Arbitrary number of days

Given a year with d days, the generalized birthday problem asks for the minimal number n(d) such that, in a set of n randomly chosen people, the probability of a birthday coincidence is at least 50%. In other words, n(d) is the minimal integer n such that

[math]\displaystyle{ 1-\left(1-\frac{1}{d}\right)\left(1-\frac{2}{d}\right)\cdots\left(1-\frac{n-1}{d}\right)\geq \frac{1}{2}. }[/math]

The classical birthday problem thus corresponds to determining n(365). The first 99 values of n(d) are given here (sequence A033810 in the OEIS):

d	1–2	3–5	6–9	10–16	17–23	24–32	33–42	43–54	55–68	69–82	83–99
n(d)	2	3	4	5	6	7	8	9	10	11	12

A similar calculation shows that n(d) = 23 when d is in the range 341–372.

A number of bounds and formulas for n(d) have been published. For any d ≥ 1, the number n(d) satisfies

[math]\displaystyle{ \frac{3-2\ln2}{6}\lt n(d)-\sqrt{2d\ln2}\leq 9-\sqrt{86\ln2}. }[/math]

These bounds are optimal in the sense that the sequence n(d) − √2d ln 2 gets arbitrarily close to

[math]\displaystyle{ \frac{3-2\ln2}{6} \approx 0.27, }[/math]

while it has

[math]\displaystyle{ 9-\sqrt{86\ln2}\approx 1.28 }[/math]

as its maximum, taken for d = 43.

The bounds are sufficiently tight to give the exact value of n(d) in most of the cases. For example, for d = 365 these bounds imply that 22.7633 < n(365) < 23.7736 and 23 is the only integer in that range. In general, it follows from these bounds that n(d) always equals either

[math]\displaystyle{ \left\lceil\sqrt{2d\ln2}\,\right\rceil \quad\text{or}\quad \left\lceil\sqrt{2d\ln2}\,\right\rceil+1 }[/math]

where ⌈ · ⌉ denotes the ceiling function. The formula

[math]\displaystyle{ n(d) = \left\lceil\sqrt{2d\ln2}\,\right\rceil }[/math]

holds for 73% of all integers d. The formula

[math]\displaystyle{ n(d) = \left\lceil\sqrt{2d\ln2}+\frac{3-2\ln2}{6}\right\rceil }[/math]

holds for almost all d, i.e., for a set of integers d with asymptotic density 1.

The formula

[math]\displaystyle{ n(d)=\left\lceil \sqrt{2d\ln2}+\frac{3-2\ln2}{6}+\frac{9-4(\ln2)^2}{72\sqrt{2d\ln2}}\right\rceil }[/math]

holds for all d ≤ 10¹⁸, but it is conjectured that there are infinitely many counterexamples to this formula.

The formula

[math]\displaystyle{ n(d)=\left\lceil \sqrt{2d\ln2}+\frac{3-2\ln2}{6}+\frac{9-4(\ln2)^2}{72\sqrt{2d\ln2}}-\frac{2(\ln2)^2}{135d}\right\rceil }[/math]

holds for all d ≤ 10¹⁸, and it is conjectured that this formula holds for all d.

More than two people sharing a birthday

It is possible to extend the problem to ask how many people in a group are necessary for there to be a greater than 50% probability that at least 3, 4, 5, etc. of the group share the same birthday.

The first few values are as follows: >50% probability of 3 people sharing a birthday - 88 people; >50% probability of 4 people sharing a birthday - 187 people (sequence A014088 in the OEIS).

Probability of a shared birthday (collision)

The birthday problem can be generalized as follows:

Given n random integers drawn from a discrete uniform distribution with range [1,d], what is the probability p(n; d) that at least two numbers are the same? (d = 365 gives the usual birthday problem.)

The generic results can be derived using the same arguments given above.

[math]\displaystyle{ \begin{align} p(n;d) &= \begin{cases} 1-\displaystyle\prod_{k=1}^{n-1}\left(1-\frac{k}{d}\right) & n\le d \\ 1 & n \gt d \end{cases} \\[8px] & \approx 1 - e^{-\frac{n(n-1)}{2d}} \\ & \approx 1 - \left( \frac{d-1}{d} \right)^\frac{n(n-1)}{2} \end{align} }[/math]

Conversely, if n(p; d) denotes the number of random integers drawn from [1,d] to obtain a probability p that at least two numbers are the same, then

[math]\displaystyle{ n(p;d)\approx \sqrt{2d \cdot \ln\left(\frac{1}{1-p}\right)}. }[/math]

The birthday problem in this more generic sense applies to hash functions: the expected number of N-bit hashes that can be generated before getting a collision is not 2^N, but rather only 2^​N⁄₂. This is exploited by birthday attacks on cryptographic hash functions and is the reason why a small number of collisions in a hash table are, for all practical purposes, inevitable.

The theory behind the birthday problem was used by Zoe Schnabel under the name of capture-recapture statistics to estimate the size of fish population in lakes.

Generalization to multiple types of people

Plot of the probability of at least one shared birthday between at least one man and one woman

The basic problem considers all trials to be of one "type". The birthday problem has been generalized to consider an arbitrary number of types. In the simplest extension there are two types of people, say m men and n women, and the problem becomes characterizing the probability of a shared birthday between at least one man and one woman. (Shared birthdays between two men or two women do not count.) The probability of no shared birthdays here is

[math]\displaystyle{ p_0 =\frac{1}{d^{m+n}} \sum_{i=1}^m \sum_{j=1}^n S_2(m,i) S_2(n,j) \prod_{k=0}^{i+j-1} d - k }[/math]

where d = 365 and S₂ are Stirling numbers of the second kind. Consequently, the desired probability is 1 − p₀.

This variation of the birthday problem is interesting because there is not a unique solution for the total number of people m + n. For example, the usual 50% probability value is realized for both a 32-member group of 16 men and 16 women and a 49-member group of 43 women and 6 men.

Other birthday problems

First match

A related question is, as people enter a room one at a time, which one is most likely to be the first to have the same birthday as someone already in the room? That is, for what n is p(n) − p(n − 1) maximum? The answer is 20—if there is a prize for first match, the best position in line is 20th.

Same birthday as you

Comparing p(n) = probability of a birthday match with q(n) = probability of matching your birthday

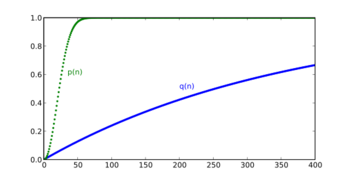
In the birthday problem, neither of the two people is chosen in advance. By contrast, the probability q(n) that someone in a room of n other people has the same birthday as a particular person (for example, you) is given by

[math]\displaystyle{ q(n) = 1 - \left( \frac{365-1}{365} \right)^n }[/math]

and for general d by

[math]\displaystyle{ q(n;d) = 1 - \left( \frac{d-1}{d} \right)^n. }[/math]

In the standard case of d = 365, substituting n = 23 gives about 6.1%, which is less than 1 chance in 16. For a greater than 50% chance that one person in a roomful of n people has the same birthday as you, n would need to be at least 253. This number is significantly higher than 365/2 = 182.5: the reason is that it is likely that there are some birthday matches among the other people in the room.

Number of people with a shared birthday

For any one person in a group of n people the probability that he or she shares his birthday with someone else is [math]\displaystyle{ q(n-1;d) }[/math], as explained above. The expected number of people with a shared (non-unique) birthday can now be calculated easily by multiplying that probability by the number of people (n), so it is:

[math]\displaystyle{ n\left(1 - \left( \frac{d-1}{d} \right)^{n-1}\right) }[/math]

(This multiplication can be done this way because of the linearity of the expected value of indicator variables). This implies that the expected number of people with a non-shared (unique) birthday is:

[math]\displaystyle{ n \left( \frac{d-1}{d} \right)^{n-1} }[/math]

Similar formulas can be derived for the expected number of people who share with three, four, etc. other people.

Number of people until every birthday is achieved

The expected number of people needed until every birthday is achieved is called the Coupon collector's problem. It can be calculated by nH_n, where H_n is the nth harmonic number. For 365 possible dates (the birthday problem), the answer is 2365.

Near matches

Another generalization is to ask for the probability of finding at least one pair in a group of n people with birthdays within k calendar days of each other, if there are d equally likely birthdays.

[math]\displaystyle{ \begin{align} p(n,k,d) &= 1 - \frac{ (d - nk -1)! }{ d^{n-1} \bigl(d - n(k+1)\bigr)!}\end{align} }[/math]

The number of people required so that the probability that some pair will have a birthday separated by k days or fewer will be higher than 50% is given in the following table:

k	n for d = 365
0	23
1	14
2	11
3	9
4	8
5	8
6	7
7	7

Thus in a group of just seven random people, it is more likely than not that two of them will have a birthday within a week of each other.

Number of days with a certain number of birthdays

Number of days with at least one birthday

The expected number of different birthdays, i.e. the number of days that are at least one person's birthday, is:

[math]\displaystyle{ d - d \left (\frac {d-1} {d} \right )^n }[/math]

This follows from the expected number of days that are no one's birthday:

[math]\displaystyle{ d \left (\frac {d-1} {d} \right )^n }[/math]

which follows from the probability that a particular day is no one's birthday, Template:Parsn , easily summed because of the linearity of the expected value.

For instance, with d = 365, you should expect about 21 different birthdays when there are 22 people, or 46 different birthdays when there are 50 people. When there are 1000 people, there will be around 341 different birthdays (24 unclaimed birthdays).

Number of days with at least two birthdays

The above can be generalized from the distribution of the number of people with their birthday on any particular day, which is a Binomial distribution with probability 1/d. Multiplying the relevant probability by d will then give the expected number of days. For example, the expected number of days which are shared; i.e. which are at least two (i.e. not zero and not one) people's birthday is:

[math]\displaystyle{ d - d \left (\frac {d-1} {d} \right )^n - d \cdot \binom{n}{1} \left (\frac {1} {d} \right )^1\left (\frac {d-1} {d} \right )^{n-1} = d - d \left (\frac {d-1} {d} \right )^n - n \left (\frac {d-1} {d} \right )^{n-1} }[/math]

Number of people who repeat a birthday

The probability that the kth integer randomly chosen from [1,d] will repeat at least one previous choice equals q(k − 1; d) above. The expected total number of times a selection will repeat a previous selection as n such integers are chosen equals

[math]\displaystyle{ \sum_{k=1}^n q(k-1;d) = n - d + d \left (\frac {d-1} {d} \right )^n }[/math]

This can be seen to equal the number of people minus the expected number of different birthdays.

Average number of people to get at least one shared birthday

In an alternative formulation of the birthday problem, one asks the average number of people required to find a pair with the same birthday. If we consider the probability function Pr[n people have at least one shared birthday], this average is determining the mean of the distribution, as opposed to the customary formulation, which asks for the median. The problem is relevant to several hashing algorithms analyzed by Donald Knuth in his book The Art of Computer Programming. It may be shown that if one samples uniformly, with replacement, from a population of size M, the number of trials required for the first repeated sampling of some individual has expected value n = 1 + Q(M), where

[math]\displaystyle{ Q(M)=\sum_{k=1}^M \frac{M!}{(M-k)! M^k}. }[/math]

The function

[math]\displaystyle{ Q(M)= 1 + \frac{M-1}{M} + \frac{(M-1)(M-2)}{M^2} + \cdots + \frac{(M-1)(M-2) \cdots 1}{M^{M-1}} }[/math]

has been studied by Srinivasa Ramanujan and has asymptotic expansion:

[math]\displaystyle{ Q(M)\sim\sqrt{\frac{\pi M}{2}}-\frac{1}{3}+\frac{1}{12}\sqrt{\frac{\pi}{2M}}-\frac{4}{135M}+\cdots. }[/math]

With M = 365 days in a year, the average number of people required to find a pair with the same birthday is n = 1 + Q(M) ≈ 24.61659, somewhat more than 23, the number required for a 50% chance. In the best case, two people will suffice; at worst, the maximum possible number of M + 1 = 366 people is needed; but on average, only 25 people are required

An analysis using indicator random variables can provide a simpler but approximate analysis of this problem. For each pair (i, j) for k people in a room, we define the indicator random variable X_ij, for [math]\displaystyle{ 1\leq i \leq j\leq k }[/math], by

[math]\displaystyle{ \begin{alignat}{2} X_{ij} & = I \{ \text{person }i\text{ and person }j\text{ have the same birthday} \} \\[10pt] & = \begin{cases} 1, & \text{if person }i\text{ and person }j\text{ have the same birthday;} \\ 0, & \text{otherwise.} \end{cases} \end{alignat} }[/math]

[math]\displaystyle{ \begin{alignat}{2} E[X_{ij}] & = \Pr \{ \text{person }i\text{ and person }j\text{ have the same birthday} \} = \frac{1}{n}. \end{alignat} }[/math]

Let X be a random variable counting the pairs of individuals with the same birthday.

[math]\displaystyle{ X =\sum_{i=1}^k \sum_{j=i+1}^k X_{ij} }[/math]

[math]\displaystyle{ \begin{alignat}{3} E[X] & = \sum_{i=1}^k \sum_{j=i+1}^k E[X_{ij}]\\[8pt] & = \binom{k}{2} \frac{1}{n}\\[8pt] & = \frac{k(k-1)}{2n} \end{alignat} }[/math]

For n = 365, if k = 28, the expected number of pairs of individuals with the same birthday is 28 × 27/2 × 365 ≈ 1.0356. Therefore, we can expect at least one matching pair with at least 28 people.

An informal demonstration of the problem can be made from the list of prime ministers of Australia, of which there have been 29 (As of 2017), in which Paul Keating, the 24th prime minister, and Edmund Barton, the first prime minister, share the same birthday, 18 January.

In the 2014 FIFA World Cup, each of the 32 squads had 23 players. An analysis of the official squad lists suggested that 16 squads had pairs of players sharing birthdays, and of these 5 squads had two pairs: Argentina, France, Iran, South Korea and Switzerland each had two pairs, and Australia, Bosnia and Herzegovina, Brazil, Cameroon, Colombia, Honduras, Netherlands, Nigeria, Russia, Spain and USA each with one pair.

Voracek, Tran and Formann showed that the majority of people markedly overestimate the number of people that is necessary to achieve a given probability of people having the same birthday, and markedly underestimate the probability of people having the same birthday when a specific sample size is given. Further results showed that psychology students and women did better on the task than casino visitors/personnel or men, but were less confident about their estimates.

Reverse problem

The reverse problem is to find, for a fixed probability p,

Taking the above formula for d = 365, one has

[math]\displaystyle{ n(p;365)\approx \sqrt{730\ln\left(\frac{1}{1-p}\right)}. }[/math]

The following table gives some sample calculations.

p	n	n↓	p(n↓)	n↑	p(n↑)
0.01	0.14178√365 = 2.70864	2	0.00274	3	0.00820
0.05	0.32029√365 = 6.11916	6	0.04046	7	0.05624
0.1	0.45904√365 = 8.77002	8	0.07434	9	0.09462
0.2	0.66805√365 = 12.76302	12	0.16702	13	0.19441
0.3	0.84460√365 = 16.13607	16	0.28360	17	0.31501
0.5	1.17741√365 = 22.49439	22	0.47570	23	0.50730
0.7	1.55176√365 = 29.64625	29	0.68097	30	0.70632
0.8	1.79412√365 = 34.27666	34	0.79532	35	0.81438
0.9	2.14597√365 = 40.99862	40	0.89123	41	0.90315
0.95	2.44775√365 = 46.76414	46	0.94825	47	0.95477
0.99	3.03485√365 = 57.98081	57	0.99012	58	0.99166

Some values falling outside the bounds have been colored to show that the approximation is not always exact.

Partition problem

A related problem is the partition problem, a variant of the knapsack problem from operations research. Some weights are put on a balance scale; each weight is an integer number of grams randomly chosen between one gram and one million grams (one tonne). The question is whether one can usually (that is, with probability close to 1) transfer the weights between the left and right arms to balance the scale. (In case the sum of all the weights is an odd number of grams, a discrepancy of one gram is allowed.) If there are only two or three weights, the answer is very clearly no; although there are some combinations which work, the majority of randomly selected combinations of three weights do not. If there are very many weights, the answer is clearly yes. The question is, how many are just sufficient? That is, what is the number of weights such that it is equally likely for it to be possible to balance them as it is to be impossible?

Often, people's intuition is that the answer is above 100000. Most people's intuition is that it is in the thousands or tens of thousands, while others feel it should at least be in the hundreds. The correct answer is 23.

The reason is that the correct comparison is to the number of partitions of the weights into left and right. There are 2^{N − 1} different partitions for N weights, and the left sum minus the right sum can be thought of as a new random quantity for each partition. The distribution of the sum of weights is approximately Gaussian, with a peak at 500000N and width 1000000√N, so that when 2^{N − 1} is approximately equal to 1000000√N the transition occurs. 2^{23 − 1} is about 4 million, while the width of the distribution is only 5 million.

In fiction

Arthur C. Clarke's 1961 novel A Fall of Moondust contains a section where the main characters, trapped underground for an indefinite amount of time, are celebrating a birthday and find themselves discussing the validity of the birthday problem. As stated by a physicist passenger: "If you have a group of more than twenty-four people, the odds are better than even that two of them have the same birthday." Eventually, out of 22 present, it is revealed that two characters share the same birthday, May 23.

Bibliography

• Abramson, M.; Moser, W. O. J. (1970). "More Birthday Surprises". American Mathematical Monthly 77 (8): 856–858. doi:10.2307/2317022. 
• Bloom, D. (1973). "A Birthday Problem". American Mathematical Monthly 80 (10): 1141–1142. doi:10.2307/2318556. 
• Kemeny, John G.; Snell, J. Laurie; Thompson, Gerald (1957). Introduction to Finite Mathematics (First ed.). 
• Klamkin, M.; Newman, D. (1967). "Extensions of the Birthday Surprise". Journal of Combinatorial Theory 3 (3): 279–282. doi:10.1016/s0021-9800(67)80075-9. 
• McKinney, E. H. (1966). "Generalized Birthday Problem". American Mathematical Monthly 73 (5): 385–387. doi:10.2307/2315408. 
• Mosteller, F. (1962). "Understanding the birthday problem". The Mathematics Teacher. Springer Series in Statistics 55 (5): 322–325. doi:10.1007/978-0-387-44956-2_21. ISBN 978-0-387-20271-6. 
• Schneps, Leila; Colmez, Coralie (2013). "Math error number 5. The case of Diana Sylvester: cold hit analysis". Math on Trial. How Numbers Get Used and Abused in the Courtroom. Basic Books. ISBN 978-0-465-03292-1. 
• Sy M. Blinder (2013). Guide to Essential Math: A Review for Physics, Chemistry and Engineering Students. Elsevier. pp. 5–6. ISBN 978-0-12-407163-6. https://books.google.com/books?id=M7TCNAEACAAJ. 

External links

• The Birthday Paradox accounting for leap year birthdays
• Weisstein, Eric W.. "Birthday Problem". http://mathworld.wolfram.com/BirthdayProblem.html. 
• A humorous article explaining the paradox
• SOCR EduMaterials activities birthday experiment
• Understanding the Birthday Problem (Better Explained)
• Eurobirthdays 2012. A birthday problem. A practical football example of the birthday paradox.
• Grime, James. "23: Birthday Probability". Numberphile. Brady Haran. http://www.numberphile.com/videos/23birthday.html. 
• Computing the probabilities of the Birthday Problem at WolframAlpha