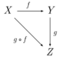Tensor-hom adjunction
In mathematics, the tensor-hom adjunction is that the tensor product [math]\displaystyle{ - \otimes X }[/math] and hom-functor [math]\displaystyle{ \operatorname{Hom}(X,-) }[/math] form an adjoint pair:
- [math]\displaystyle{ \operatorname{Hom}(Y \otimes X, Z) \cong \operatorname{Hom}(Y,\operatorname{Hom}(X,Z)). }[/math]
This is made more precise below. The order of terms in the phrase "tensor-hom adjunction" reflects their relationship: tensor is the left adjoint, while hom is the right adjoint.
General statement
Say R and S are (possibly noncommutative) rings, and consider the right module categories (an analogous statement holds for left modules):
- [math]\displaystyle{ \mathcal{C} = \mathrm{Mod}_S\quad \text{and} \quad \mathcal{D} = \mathrm{Mod}_R . }[/math]
Fix an [math]\displaystyle{ (R,S) }[/math]-bimodule [math]\displaystyle{ X }[/math] and define functors [math]\displaystyle{ F \colon \mathcal D \rightarrow \mathcal C }[/math] and [math]\displaystyle{ G \colon \mathcal C \rightarrow \mathcal D }[/math] as follows:
- [math]\displaystyle{ F(Y) = Y \otimes_R X \quad \text{for } Y \in \mathcal{D} }[/math]
- [math]\displaystyle{ G(Z) = \operatorname{Hom}_S (X, Z) \quad \text{for } Z \in \mathcal{C} }[/math]
Then [math]\displaystyle{ F }[/math] is left adjoint to [math]\displaystyle{ G }[/math]. This means there is a natural isomorphism
- [math]\displaystyle{ \operatorname{Hom}_S (Y \otimes_R X, Z) \cong \operatorname{Hom}_R (Y , \operatorname{Hom}_S (X, Z)). }[/math]
This is actually an isomorphism of abelian groups. More precisely, if [math]\displaystyle{ Y }[/math] is an [math]\displaystyle{ (A,R) }[/math]-bimodule and [math]\displaystyle{ Z }[/math] is a [math]\displaystyle{ (B,S) }[/math]-bimodule, then this is an isomorphism of [math]\displaystyle{ (B,A) }[/math]-bimodules. This is one of the motivating examples of the structure in a closed bicategory.[1]
Counit and unit
Like all adjunctions, the tensor-hom adjunction can be described by its counit and unit natural transformations. Using the notation from the previous section, the counit
- [math]\displaystyle{ \varepsilon : FG \to 1_{\mathcal{C}} }[/math]
has components
- [math]\displaystyle{ \varepsilon_Z : \operatorname{Hom}_S (X, Z) \otimes_R X \to Z }[/math]
given by evaluation: For
- [math]\displaystyle{ \phi \in \operatorname{Hom}_S (X, Z) \quad \text{and} \quad x \in X, }[/math]
- [math]\displaystyle{ \varepsilon(\phi \otimes x) = \phi(x). }[/math]
The components of the unit
- [math]\displaystyle{ \eta : 1_{\mathcal{D}} \to GF }[/math]
- [math]\displaystyle{ \eta_Y : Y \to \operatorname{Hom}_S (X, Y \otimes_R X) }[/math]
are defined as follows: For [math]\displaystyle{ y }[/math] in [math]\displaystyle{ Y }[/math],
- [math]\displaystyle{ \eta_Y(y) \in \operatorname{Hom}_S (X, Y \otimes_R X) }[/math]
is a right [math]\displaystyle{ S }[/math]-module homomorphism given by
- [math]\displaystyle{ \eta_Y(y)(t) = y \otimes t \quad \text{for } t \in X. }[/math]
The counit and unit equations can now be explicitly verified. For [math]\displaystyle{ Y }[/math] in [math]\displaystyle{ \mathcal{D} }[/math],
- [math]\displaystyle{ \varepsilon_{FY}\circ F(\eta_Y) : Y \otimes_R X \to \operatorname{Hom}_S (X , Y \otimes_R X) \otimes_R X \to Y \otimes_R X }[/math]
is given on simple tensors of [math]\displaystyle{ Y \otimes X }[/math] by
- [math]\displaystyle{ \varepsilon_{FY}\circ F(\eta_Y)(y \otimes x) = \eta_Y(y)(x) = y \otimes x. }[/math]
Likewise,
- [math]\displaystyle{ G(\varepsilon_Z)\circ\eta_{GZ} : \operatorname{Hom}_S (X, Z) \to \operatorname{Hom}_S (X, \operatorname{Hom}_S (X , Z) \otimes_R X) \to \operatorname{Hom}_S (X, Z). }[/math]
For [math]\displaystyle{ \phi }[/math] in [math]\displaystyle{ \operatorname{Hom}_S (X, Z) }[/math],
- [math]\displaystyle{ G(\varepsilon_Z)\circ\eta_{GZ}(\phi) }[/math]
is a right [math]\displaystyle{ S }[/math]-module homomorphism defined by
- [math]\displaystyle{ G(\varepsilon_Z)\circ\eta_{GZ}(\phi)(x) = \varepsilon_{Z}(\phi \otimes x) = \phi(x) }[/math]
and therefore
- [math]\displaystyle{ G(\varepsilon_Z)\circ\eta_{GZ}(\phi) = \phi. }[/math]
The Ext and Tor functors
The Hom functor [math]\displaystyle{ \hom(X,-) }[/math] commutes with arbitrary limits, while the tensor product [math]\displaystyle{ -\otimes X }[/math] functor commutes with arbitrary colimits that exist in their domain category. However, in general, [math]\displaystyle{ \hom(X,-) }[/math] fails to commute with colimits, and [math]\displaystyle{ -\otimes X }[/math] fails to commute with limits; this failure occurs even among finite limits or colimits. This failure to preserve short exact sequences motivates the definition of the Ext functor and the Tor functor.
See also
References
- ↑ May, J.P.; Sigurdsson, J. (2006). Parametrized Homotopy Theory. A.M.S.. p. 253. ISBN 0-8218-3922-5.
- Bourbaki, Nicolas (1989), Elements of mathematics, Algebra I, Springer-Verlag, ISBN 3-540-64243-9
 |