Function approximation

Short description: Approximating an arbitrary function with a well-behaved one

Several progressively more accurate approximations of the step function.

An asymmetrical Gaussian function fit to a noisy curve using regression.

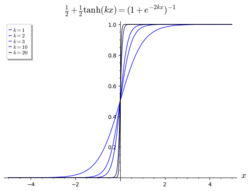
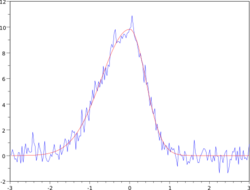
In general, a function approximation problem asks us to select a function among a well-defined class that closely matches ("approximates") a target function in a task-specific way. The need for function approximations arises in many branches of applied mathematics, and computer science in particular, such as predicting the growth of microbes in microbiology. Function approximations are used where theoretical models are unavailable or hard to compute.

One can distinguish two major classes of function approximation problems: First, for known target functions approximation theory is the branch of numerical analysis that investigates how certain known functions (for example, special functions) can be approximated by a specific class of functions (for example, polynomials or rational functions) that often have desirable properties (inexpensive computation, continuity, integral and limit values, etc.).

Second, the target function, call it g, may be unknown; instead of an explicit formula, only a set of points of the form (x, g(x)) is provided. Depending on the structure of the domain and codomain of g, several techniques for approximating g may be applicable. For example, if g is an operation on the real numbers, techniques of interpolation, extrapolation, regression analysis, and curve fitting can be used. If the codomain (range or target set) of g is a finite set, one is dealing with a classification problem instead.

To some extent, the different problems (regression, classification, fitness approximation) have received a unified treatment in statistical learning theory, where they are viewed as supervised learning problems.

See also

• Approximation theory
• Fitness approximation
• Kriging
• Least squares (function approximation)
• Radial basis function network