Implicit function theorem
| Part of a series of articles about |
| Calculus |
|---|
In multivariable calculus, the implicit function theorem[lower-alpha 1] is a tool that allows relations to be converted to functions of several real variables. It does so by representing the relation as the graph of a function. There may not be a single function whose graph can represent the entire relation, but there may be such a function on a restriction of the domain of the relation. The implicit function theorem gives a sufficient condition to ensure that there is such a function.
More precisely, given a system of m equations fi (x1, ..., xn, y1, ..., ym) = 0, i = 1, ..., m (often abbreviated into F(x, y) = 0), the theorem states that, under a mild condition on the partial derivatives (with respect to each yi ) at a point, the m variables yi are differentiable functions of the xj in some neighborhood of the point. As these functions can generally not be expressed in closed form, they are implicitly defined by the equations, and this motivated the name of the theorem.[1]
In other words, under a mild condition on the partial derivatives, the set of zeros of a system of equations is locally the graph of a function.
History
Augustin-Louis Cauchy (1789–1857) is credited with the first rigorous form of the implicit function theorem. Ulisse Dini (1845–1918) generalized the real-variable version of the implicit function theorem to the context of functions of any number of real variables.[2]
First example
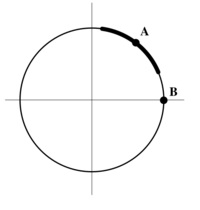
If we define the function f(x, y) = x2 + y2, then the equation f(x, y) = 1 cuts out the unit circle as the level set {(x, y) | f(x, y) = 1}. There is no way to represent the unit circle as the graph of a function of one variable y = g(x) because for each choice of x ∈ (−1, 1), there are two choices of y, namely [math]\displaystyle{ \pm\sqrt{1-x^2} }[/math].
However, it is possible to represent part of the circle as the graph of a function of one variable. If we let [math]\displaystyle{ g_1(x) = \sqrt{1-x^2} }[/math] for −1 ≤ x ≤ 1, then the graph of y = g1(x) provides the upper half of the circle. Similarly, if [math]\displaystyle{ g_2(x) = -\sqrt{1-x^2} }[/math], then the graph of y = g2(x) gives the lower half of the circle.
The purpose of the implicit function theorem is to tell us that functions like g1(x) and g2(x) almost always exist, even in situations where we cannot write down explicit formulas. It guarantees that g1(x) and g2(x) are differentiable, and it even works in situations where we do not have a formula for f(x, y).
Definitions
Let [math]\displaystyle{ f: \R^{n+m} \to \R^m }[/math] be a continuously differentiable function. We think of [math]\displaystyle{ \R^{n+m} }[/math] as the Cartesian product [math]\displaystyle{ \R^n\times\R^m, }[/math] and we write a point of this product as [math]\displaystyle{ (\mathbf{x}, \mathbf{y}) = (x_1,\ldots, x_n, y_1, \ldots y_m). }[/math] Starting from the given function [math]\displaystyle{ f }[/math], our goal is to construct a function [math]\displaystyle{ g: \R^n \to \R^m }[/math] whose graph [math]\displaystyle{ (\textbf{x}, g(\textbf{x})) }[/math] is precisely the set of all [math]\displaystyle{ (\textbf{x}, \textbf{y}) }[/math] such that [math]\displaystyle{ f(\textbf{x}, \textbf{y}) = \textbf{0} }[/math].
As noted above, this may not always be possible. We will therefore fix a point [math]\displaystyle{ (\textbf{a}, \textbf{b}) = (a_1, \dots, a_n, b_1, \dots, b_m) }[/math] which satisfies [math]\displaystyle{ f(\textbf{a}, \textbf{b}) = \textbf{0} }[/math], and we will ask for a [math]\displaystyle{ g }[/math] that works near the point [math]\displaystyle{ (\textbf{a}, \textbf{b}) }[/math]. In other words, we want an open set [math]\displaystyle{ U \subset \R^n }[/math] containing [math]\displaystyle{ \textbf{a} }[/math], an open set [math]\displaystyle{ V \subset \R^m }[/math] containing [math]\displaystyle{ \textbf{b} }[/math], and a function [math]\displaystyle{ g : U \to V }[/math] such that the graph of [math]\displaystyle{ g }[/math] satisfies the relation [math]\displaystyle{ f = \textbf{0} }[/math] on [math]\displaystyle{ U\times V }[/math], and that no other points within [math]\displaystyle{ U \times V }[/math] do so. In symbols,
[math]\displaystyle{ \{ (\mathbf{x}, g(\mathbf{x})) \mid \mathbf x \in U \} = \{ (\mathbf{x}, \mathbf{y})\in U \times V \mid f(\mathbf{x}, \mathbf{y}) = \mathbf{0} \}. }[/math]
To state the implicit function theorem, we need the Jacobian matrix of [math]\displaystyle{ f }[/math], which is the matrix of the partial derivatives of [math]\displaystyle{ f }[/math]. Abbreviating [math]\displaystyle{ (a_1, \dots, a_n, b_1, \dots, b_m) }[/math] to [math]\displaystyle{ (\textbf{a}, \textbf{b}) }[/math], the Jacobian matrix is
[math]\displaystyle{ (Df)(\mathbf{a},\mathbf{b}) = \left[\begin{array}{ccc|ccc} \frac{\partial f_1}{\partial x_1}(\mathbf{a},\mathbf{b}) & \cdots & \frac{\partial f_1}{\partial x_n}(\mathbf{a},\mathbf{b}) & \frac{\partial f_1}{\partial y_1}(\mathbf{a},\mathbf{b}) & \cdots & \frac{\partial f_1}{\partial y_m}(\mathbf{a},\mathbf{b}) \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1}(\mathbf{a},\mathbf{b}) & \cdots & \frac{\partial f_m}{\partial x_n}(\mathbf{a},\mathbf{b}) & \frac{\partial f_m}{\partial y_1}(\mathbf{a},\mathbf{b}) & \cdots & \frac{\partial f_m}{\partial y_m}(\mathbf{a},\mathbf{b}) \end{array}\right] = \left[\begin{array}{c|c} X & Y \end{array}\right] }[/math]
where [math]\displaystyle{ X }[/math] is the matrix of partial derivatives in the variables [math]\displaystyle{ x_i }[/math] and [math]\displaystyle{ Y }[/math] is the matrix of partial derivatives in the variables [math]\displaystyle{ y_j }[/math]. The implicit function theorem says that if [math]\displaystyle{ Y }[/math] is an invertible matrix, then there are [math]\displaystyle{ U }[/math], [math]\displaystyle{ V }[/math], and [math]\displaystyle{ g }[/math] as desired. Writing all the hypotheses together gives the following statement.
Statement of the theorem
Let [math]\displaystyle{ f: \R^{n+m} \to \R^m }[/math] be a continuously differentiable function, and let [math]\displaystyle{ \R^{n+m} }[/math] have coordinates [math]\displaystyle{ (\textbf{x}, \textbf{y}) }[/math]. Fix a point [math]\displaystyle{ (\textbf{a}, \textbf{b}) = (a_1,\dots,a_n, b_1,\dots, b_m) }[/math] with [math]\displaystyle{ f(\textbf{a}, \textbf{b}) = \mathbf{0} }[/math], where [math]\displaystyle{ \mathbf{0} \in \R^m }[/math] is the zero vector. If the Jacobian matrix (this is the right-hand panel of the Jacobian matrix shown in the previous section): [math]\displaystyle{ J_{f, \mathbf{y}} (\mathbf{a}, \mathbf{b}) = \left [ \frac{\partial f_i}{\partial y_j} (\mathbf{a}, \mathbf{b}) \right ] }[/math] is invertible, then there exists an open set [math]\displaystyle{ U \subset \R^n }[/math] containing [math]\displaystyle{ \textbf{a} }[/math] such that there exists a unique continuously differentiable function [math]\displaystyle{ g: U \to \R^m }[/math] such that [math]\displaystyle{ g(\mathbf{a}) = \mathbf{b} }[/math], and [math]\displaystyle{ f(\mathbf{x}, g(\mathbf{x})) = \mathbf{0} ~ \text{for all} ~ \mathbf{x}\in U }[/math]. Moreover, denoting the left-hand panel of the Jacobian matrix shown in the previous section as: [math]\displaystyle{ J_{f, \mathbf{x}} (\mathbf{a}, \mathbf{b}) = \left [ \frac{\partial f_i}{\partial x_j} (\mathbf{a}, \mathbf{b}) \right ], }[/math] the Jacobian matrix of partial derivatives of [math]\displaystyle{ g }[/math] in [math]\displaystyle{ U }[/math] is given by the matrix product:[3] [math]\displaystyle{ \left[\frac{\partial g_i}{\partial x_j} (\mathbf{x})\right]_{m\times n} =- \left [ J_{f, \mathbf{y}}(\mathbf{x}, g(\mathbf{x})) \right ]_{m \times m} ^{-1} \, \left [ J_{f, \mathbf{x}}(\mathbf{x}, g(\mathbf{x})) \right ]_{m \times n} }[/math]
Higher derivatives
If, moreover, [math]\displaystyle{ f }[/math] is analytic or continuously differentiable [math]\displaystyle{ k }[/math] times in a neighborhood of [math]\displaystyle{ (\textbf{a}, \textbf{b}) }[/math], then one may choose [math]\displaystyle{ U }[/math] in order that the same holds true for [math]\displaystyle{ g }[/math] inside [math]\displaystyle{ U }[/math]. [4] In the analytic case, this is called the analytic implicit function theorem.
Proof for 2D case
Suppose [math]\displaystyle{ F:\R^2 \to \R }[/math] is a continuously differentiable function defining a curve [math]\displaystyle{ F(\mathbf{r}) = F(x,y) = 0 }[/math]. Let [math]\displaystyle{ (x_0, y_0) }[/math] be a point on the curve. The statement of the theorem above can be rewritten for this simple case as follows:
Theorem — If [math]\displaystyle{ \left. \frac{\partial F}{ \partial y} \right|_{(x_0, y_0)} \neq 0 }[/math] then in a neighbourhood of the point [math]\displaystyle{ (x_0, y_0) }[/math] we can write [math]\displaystyle{ y = f(x) }[/math], where [math]\displaystyle{ f }[/math] is a real function.
Proof. Since F is differentiable we write the differential of F through partial derivatives: [math]\displaystyle{ \mathrm{d} F = \operatorname{grad} F \cdot \mathrm{d}\mathbf{r} = \frac{\partial F}{\partial x} \mathrm{d} x + \frac{\partial F}{\partial y}\mathrm{d}y. }[/math]
Since we are restricted to movement on the curve [math]\displaystyle{ F = 0 }[/math] and by assumption [math]\displaystyle{ \tfrac{\partial F}{\partial y} \neq 0 }[/math] around the point [math]\displaystyle{ (x_0, y_0) }[/math] (since [math]\displaystyle{ \tfrac{\partial F}{\partial y} }[/math] is continuous at [math]\displaystyle{ (x_0, y_0) }[/math] and [math]\displaystyle{ \left. \tfrac{\partial F}{ \partial y} \right|_{(x_0, y_0)} \neq 0 }[/math]). Therefore we have a first-order ordinary differential equation: [math]\displaystyle{ \partial_x F \mathrm{d} x + \partial_y F \mathrm{d} y = 0, \quad y(x_0) = y_0 }[/math]
Now we are looking for a solution to this ODE in an open interval around the point [math]\displaystyle{ (x_0, y_0) }[/math] for which, at every point in it, [math]\displaystyle{ \partial_y F \neq 0 }[/math]. Since F is continuously differentiable and from the assumption we have [math]\displaystyle{ |\partial_x F| \lt \infty, |\partial_y F| \lt \infty, \partial_y F \neq 0. }[/math]
From this we know that [math]\displaystyle{ \tfrac{\partial_x F}{\partial_y F} }[/math] is continuous and bounded on both ends. From here we know that [math]\displaystyle{ -\tfrac{\partial_x F}{\partial_y F} }[/math] is Lipschitz continuous in both x and y. Therefore, by Cauchy-Lipschitz theorem, there exists unique y(x) that is the solution to the given ODE with the initial conditions. Q.E.D.
The circle example
Let us go back to the example of the unit circle. In this case n = m = 1 and [math]\displaystyle{ f(x,y) = x^2 + y^2 - 1 }[/math]. The matrix of partial derivatives is just a 1 × 2 matrix, given by [math]\displaystyle{ (Df)(a,b) = \begin{bmatrix} \dfrac{\partial f}{\partial x}(a,b) & \dfrac{\partial f}{\partial y}(a,b) \end{bmatrix} = \begin{bmatrix} 2a & 2b \end{bmatrix} }[/math]
Thus, here, the Y in the statement of the theorem is just the number 2b; the linear map defined by it is invertible if and only if b ≠ 0. By the implicit function theorem we see that we can locally write the circle in the form y = g(x) for all points where y ≠ 0. For (±1, 0) we run into trouble, as noted before. The implicit function theorem may still be applied to these two points, by writing x as a function of y, that is, [math]\displaystyle{ x = h(y) }[/math]; now the graph of the function will be [math]\displaystyle{ \left(h(y), y\right) }[/math], since where b = 0 we have a = 1, and the conditions to locally express the function in this form are satisfied.
The implicit derivative of y with respect to x, and that of x with respect to y, can be found by totally differentiating the implicit function [math]\displaystyle{ x^2+y^2-1 }[/math] and equating to 0: [math]\displaystyle{ 2x\, dx+2y\, dy = 0, }[/math] giving [math]\displaystyle{ \frac{dy}{dx}=-\frac{x}{y} }[/math] and [math]\displaystyle{ \frac{dx}{dy} = -\frac{y}{x}. }[/math]
Application: change of coordinates
Suppose we have an m-dimensional space, parametrised by a set of coordinates [math]\displaystyle{ (x_1,\ldots,x_m) }[/math]. We can introduce a new coordinate system [math]\displaystyle{ (x'_1,\ldots,x'_m) }[/math] by supplying m functions [math]\displaystyle{ h_1\ldots h_m }[/math] each being continuously differentiable. These functions allow us to calculate the new coordinates [math]\displaystyle{ (x'_1,\ldots,x'_m) }[/math] of a point, given the point's old coordinates [math]\displaystyle{ (x_1,\ldots,x_m) }[/math] using [math]\displaystyle{ x'_1=h_1(x_1,\ldots,x_m), \ldots, x'_m=h_m(x_1,\ldots,x_m) }[/math]. One might want to verify if the opposite is possible: given coordinates [math]\displaystyle{ (x'_1,\ldots,x'_m) }[/math], can we 'go back' and calculate the same point's original coordinates [math]\displaystyle{ (x_1,\ldots,x_m) }[/math]? The implicit function theorem will provide an answer to this question. The (new and old) coordinates [math]\displaystyle{ (x'_1,\ldots,x'_m, x_1,\ldots,x_m) }[/math] are related by f = 0, with [math]\displaystyle{ f(x'_1,\ldots,x'_m,x_1,\ldots, x_m)=(h_1(x_1,\ldots, x_m)-x'_1,\ldots , h_m(x_1,\ldots, x_m)-x'_m). }[/math] Now the Jacobian matrix of f at a certain point (a, b) [ where [math]\displaystyle{ a=(x'_1,\ldots,x'_m), b=(x_1,\ldots,x_m) }[/math] ] is given by [math]\displaystyle{ (Df)(a,b) = \left [\begin{matrix} -1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & -1 \end{matrix}\left| \begin{matrix} \frac{\partial h_1}{\partial x_1}(b) & \cdots & \frac{\partial h_1}{\partial x_m}(b)\\ \vdots & \ddots & \vdots\\ \frac{\partial h_m}{\partial x_1}(b) & \cdots & \frac{\partial h_m}{\partial x_m}(b)\\ \end{matrix} \right.\right] = [-I_m |J ]. }[/math] where Im denotes the m × m identity matrix, and J is the m × m matrix of partial derivatives, evaluated at (a, b). (In the above, these blocks were denoted by X and Y. As it happens, in this particular application of the theorem, neither matrix depends on a.) The implicit function theorem now states that we can locally express [math]\displaystyle{ (x_1,\ldots,x_m) }[/math] as a function of [math]\displaystyle{ (x'_1,\ldots,x'_m) }[/math] if J is invertible. Demanding J is invertible is equivalent to det J ≠ 0, thus we see that we can go back from the primed to the unprimed coordinates if the determinant of the Jacobian J is non-zero. This statement is also known as the inverse function theorem.
Example: polar coordinates
As a simple application of the above, consider the plane, parametrised by polar coordinates (R, θ). We can go to a new coordinate system (cartesian coordinates) by defining functions x(R, θ) = R cos(θ) and y(R, θ) = R sin(θ). This makes it possible given any point (R, θ) to find corresponding Cartesian coordinates (x, y). When can we go back and convert Cartesian into polar coordinates? By the previous example, it is sufficient to have det J ≠ 0, with [math]\displaystyle{ J =\begin{bmatrix} \frac{\partial x(R,\theta)}{\partial R} & \frac{\partial x(R,\theta)}{\partial \theta} \\ \frac{\partial y(R,\theta)}{\partial R} & \frac{\partial y(R,\theta)}{\partial \theta} \\ \end{bmatrix}= \begin{bmatrix} \cos \theta & -R \sin \theta \\ \sin \theta & R \cos \theta \end{bmatrix}. }[/math] Since det J = R, conversion back to polar coordinates is possible if R ≠ 0. So it remains to check the case R = 0. It is easy to see that in case R = 0, our coordinate transformation is not invertible: at the origin, the value of θ is not well-defined.
Generalizations
Banach space version
Based on the inverse function theorem in Banach spaces, it is possible to extend the implicit function theorem to Banach space valued mappings.[5][6]
Let X, Y, Z be Banach spaces. Let the mapping f : X × Y → Z be continuously Fréchet differentiable. If [math]\displaystyle{ (x_0,y_0)\in X\times Y }[/math], [math]\displaystyle{ f(x_0,y_0)=0 }[/math], and [math]\displaystyle{ y\mapsto Df(x_0,y_0)(0,y) }[/math] is a Banach space isomorphism from Y onto Z, then there exist neighbourhoods U of x0 and V of y0 and a Fréchet differentiable function g : U → V such that f(x, g(x)) = 0 and f(x, y) = 0 if and only if y = g(x), for all [math]\displaystyle{ (x,y)\in U\times V }[/math].
Implicit functions from non-differentiable functions
Various forms of the implicit function theorem exist for the case when the function f is not differentiable. It is standard that local strict monotonicity suffices in one dimension.[7] The following more general form was proven by Kumagai based on an observation by Jittorntrum.[8][9]
Consider a continuous function [math]\displaystyle{ f : \R^n \times \R^m \to \R^n }[/math] such that [math]\displaystyle{ f(x_0, y_0) = 0 }[/math]. If there exist open neighbourhoods [math]\displaystyle{ A \subset \R^n }[/math] and [math]\displaystyle{ B \subset \R^m }[/math] of x0 and y0, respectively, such that, for all y in B, [math]\displaystyle{ f(\cdot, y) : A \to \R^n }[/math] is locally one-to-one then there exist open neighbourhoods [math]\displaystyle{ A_0 \subset \R^n }[/math] and [math]\displaystyle{ B_0 \subset \R^m }[/math] of x0 and y0, such that, for all [math]\displaystyle{ y \in B_0 }[/math], the equation f(x, y) = 0 has a unique solution [math]\displaystyle{ x = g(y) \in A_0, }[/math] where g is a continuous function from B0 into A0.
Collapsing manifolds
Perelman’s collapsing theorem for 3-manifolds, the capstone of his proof of Thurston's geometrization conjecture, can be understood as an extension of the implicit function theorem.[10]
See also
- Inverse function theorem
- Constant rank theorem: Both the implicit function theorem and the inverse function theorem can be seen as special cases of the constant rank theorem.
Notes
- ↑ Also called Dini's theorem by the Pisan school in Italy. In the English-language literature, Dini's theorem is a different theorem in mathematical analysis.
References
- ↑ Chiang, Alpha C. (1984). Fundamental Methods of Mathematical Economics (3rd ed.). McGraw-Hill. pp. 204–206. ISBN 0-07-010813-7. https://archive.org/details/fundamentalmetho0000chia_b4p1/page/204.
- ↑ Krantz, Steven; Parks, Harold (2003). The Implicit Function Theorem. Modern Birkhauser Classics. Birkhauser. ISBN 0-8176-4285-4. https://archive.org/details/implicitfunction0000kran.
- ↑ de Oliveira, Oswaldo (2013). "The Implicit and Inverse Function Theorems: Easy Proofs". Real Anal. Exchange 39 (1): 214–216. doi:10.14321/realanalexch.39.1.0207.
- ↑ Fritzsche, K.; Grauert, H. (2002). From Holomorphic Functions to Complex Manifolds. Springer. p. 34. ISBN 9780387953953. https://books.google.com/books?id=jSeRz36zXIMC&pg=PA34.
- ↑ Lang, Serge (1999). Fundamentals of Differential Geometry. Graduate Texts in Mathematics. New York: Springer. pp. 15–21. ISBN 0-387-98593-X. https://archive.org/details/fundamentalsdiff00lang_678.
- ↑ Edwards, Charles Henry (1994). Advanced Calculus of Several Variables. Mineola, New York: Dover Publications. pp. 417–418. ISBN 0-486-68336-2.
- ↑ Hazewinkel, Michiel, ed. (2001), "Implicit function", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=i/i050310
- ↑ Jittorntrum, K. (1978). "An Implicit Function Theorem". Journal of Optimization Theory and Applications 25 (4): 575–577. doi:10.1007/BF00933522.
- ↑ Kumagai, S. (1980). "An implicit function theorem: Comment". Journal of Optimization Theory and Applications 31 (2): 285–288. doi:10.1007/BF00934117.
- ↑ Cao, Jianguo; Ge, Jian (2011). "A simple proof of Perelman's collapsing theorem for 3-manifolds". J. Geom. Anal. 21 (4): 807–869. doi:10.1007/s12220-010-9169-5.
Further reading
- Allendoerfer, Carl B. (1974). "Theorems about Differentiable Functions". Calculus of Several Variables and Differentiable Manifolds. New York: Macmillan. pp. 54–88. ISBN 0-02-301840-2.
- Binmore, K. G. (1983). "Implicit Functions". Calculus. New York: Cambridge University Press. pp. 198–211. ISBN 0-521-28952-1. https://books.google.com/books?id=K8RfQgAACAAJ&pg=PA198.
- Loomis, Lynn H.; Sternberg, Shlomo (1990). Advanced Calculus (Revised ed.). Boston: Jones and Bartlett. pp. 164–171. ISBN 0-86720-122-3. https://archive.org/details/advancedcalculus0000loom.
- Protter, Murray H.; Morrey, Charles B. Jr. (1985). "Implicit Function Theorems. Jacobians". Intermediate Calculus (2nd ed.). New York: Springer. pp. 390–420. ISBN 0-387-96058-9. https://books.google.com/books?id=3lTmBwAAQBAJ&pg=PA390.
 |

