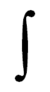Differential (infinitesimal)

Short description: Infinitesimal quantity in calculus

The term differential is used in calculus to refer to an infinitesimal (infinitely small) change in some varying quantity. For example, if x is a variable, then a change in the value of x is often denoted Δx (pronounced delta x). The differential dx represents an infinitely small change in the variable x. The idea of an infinitely small or infinitely slow change is, intuitively, extremely useful, and there are a number of ways to make the notion mathematically precise.

Using calculus, it is possible to relate the infinitely small changes of various variables to each other mathematically using derivatives. If y is a function of x, then the differential dy of y is related to dx by the formula

[math]\displaystyle{ dy = \frac{dy}{dx} \,dx, }[/math]

where [math]\displaystyle{ \frac{dy}{dx} \, }[/math]denotes the derivative of y with respect to x. This formula summarizes the intuitive idea that the derivative of y with respect to x is the limit of the ratio of differences Δy/Δx as Δx becomes infinitesimal.

There are several approaches for making the notion of differentials mathematically precise.

1. Differentials as linear maps. This approach underlies the definition of the derivative and the exterior derivative in differential geometry.
2. Differentials as nilpotent elements of commutative rings. This approach is popular in algebraic geometry.
3. Differentials in smooth models of set theory. This approach is known as synthetic differential geometry or smooth infinitesimal analysis and is closely related to the algebraic geometric approach, except that ideas from topos theory are used to hide the mechanisms by which nilpotent infinitesimals are introduced.
4. Differentials as infinitesimals in hyperreal number systems, which are extensions of the real numbers that contain invertible infinitesimals and infinitely large numbers. This is the approach of nonstandard analysis pioneered by Abraham Robinson.

These approaches are very different from each other, but they have in common the idea of being quantitative, i.e., saying not just that a differential is infinitely small, but how small it is.

History and usage

Infinitesimal quantities played a significant role in the development of calculus. Archimedes used them, even though he didn't believe that arguments involving infinitesimals were rigorous. Isaac Newton referred to them as fluxions. However, it was Gottfried Leibniz who coined the term differentials for infinitesimal quantities and introduced the notation for them which is still used today.

In Leibniz's notation, if x is a variable quantity, then dx denotes an infinitesimal change in the variable x. Thus, if y is a function of x, then the derivative of y with respect to x is often denoted dy/dx, which would otherwise be denoted (in the notation of Newton or Lagrange) ẏ or y′. The use of differentials in this form attracted much criticism, for instance in the famous pamphlet The Analyst by Bishop Berkeley. Nevertheless, the notation has remained popular because it suggests strongly the idea that the derivative of y at x is its instantaneous rate of change (the slope of the graph's tangent line), which may be obtained by taking the limit of the ratio Δy/Δx of the change in y over the change in x, as the change in x becomes arbitrarily small. Differentials are also compatible with dimensional analysis, where a differential such as dx has the same dimensions as the variable x.

Differentials are also used in the notation for integrals because an integral can be regarded as an infinite sum of infinitesimal quantities: the area under a graph is obtained by subdividing the graph into infinitely thin strips and summing their areas. In an expression such as

[math]\displaystyle{ \int f(x) \,dx, }[/math]

the integral sign (which is a modified long s) denotes the infinite sum, f(x) denotes the "height" of a thin strip, and the differential dx denotes its infinitely thin width.

Differentials as linear maps

There is a simple way to make precise sense of differentials by regarding them as linear maps. To illustrate, suppose [math]\displaystyle{ f(x) }[/math] is a real-valued function on [math]\displaystyle{ \mathbb{R} }[/math]. We can reinterpret the variable [math]\displaystyle{ x }[/math] in [math]\displaystyle{ f(x) }[/math] as being a function rather than a number, namely the identity map on the real line, which takes a real number [math]\displaystyle{ p }[/math] to itself: [math]\displaystyle{ x(p)=p }[/math]. Then [math]\displaystyle{ f(x) }[/math] is the composite of [math]\displaystyle{ f }[/math] with [math]\displaystyle{ x }[/math], whose value at [math]\displaystyle{ p }[/math] is [math]\displaystyle{ f(x(p))=f(p) }[/math]. The differential [math]\displaystyle{ \operatorname{d}f }[/math] (which of course depends on [math]\displaystyle{ f }[/math]) is then a function whose value at [math]\displaystyle{ p }[/math] (usually denoted [math]\displaystyle{ df_p }[/math]) is not a number, but a linear map from [math]\displaystyle{ \mathbb{R} }[/math] to [math]\displaystyle{ \mathbb{R} }[/math]. Since a linear map from [math]\displaystyle{ \mathbb{R} }[/math] to [math]\displaystyle{ \mathbb{R} }[/math] is given by a [math]\displaystyle{ 1\times 1 }[/math] matrix, it is essentially the same thing as a number, but the change in the point of view allows us to think of [math]\displaystyle{ df_p }[/math] as an infinitesimal and compare it with the standard infinitesimal [math]\displaystyle{ dx_p }[/math], which is again just the identity map from [math]\displaystyle{ \mathbb{R} }[/math] to [math]\displaystyle{ \mathbb{R} }[/math] (a [math]\displaystyle{ 1\times 1 }[/math] matrix with entry [math]\displaystyle{ 1 }[/math]). The identity map has the property that if [math]\displaystyle{ \varepsilon }[/math] is very small, then [math]\displaystyle{ dx_p(\varepsilon) }[/math] is very small, which enables us to regard it as infinitesimal. The differential [math]\displaystyle{ df_p }[/math] has the same property, because it is just a multiple of [math]\displaystyle{ dx_p }[/math], and this multiple is the derivative [math]\displaystyle{ f'(p) }[/math] by definition. We therefore obtain that [math]\displaystyle{ df_p=f'(p)\,dx_p }[/math], and hence [math]\displaystyle{ df=f'\,dx }[/math]. Thus we recover the idea that [math]\displaystyle{ f' }[/math] is the ratio of the differentials [math]\displaystyle{ df }[/math] and [math]\displaystyle{ dx }[/math].

This would just be a trick were it not for the fact that:

1. it captures the idea of the derivative of [math]\displaystyle{ f }[/math] at [math]\displaystyle{ p }[/math] as the best linear approximation to [math]\displaystyle{ f }[/math] at [math]\displaystyle{ p }[/math];
2. it has many generalizations.

For instance, if [math]\displaystyle{ f }[/math] is a function from [math]\displaystyle{ \mathbb{R}^n }[/math] to [math]\displaystyle{ \mathbb{R} }[/math], then we say that [math]\displaystyle{ f }[/math] is differentiable at [math]\displaystyle{ p\in\mathbb{R}^n }[/math] if there is a linear map [math]\displaystyle{ df_p }[/math] from [math]\displaystyle{ \mathbb{R}^n }[/math] to [math]\displaystyle{ \mathbb{R} }[/math] such that for any [math]\displaystyle{ \varepsilon\gt 0 }[/math], there is a neighbourhood [math]\displaystyle{ N }[/math] of [math]\displaystyle{ p }[/math] such that for [math]\displaystyle{ x\in N }[/math],

[math]\displaystyle{ \left|f(x) - f(p) - df_p(x-p)\right| \lt \varepsilon \left|x-p\right| . }[/math]

We can now use the same trick as in the one-dimensional case and think of the expression [math]\displaystyle{ f(x^1, x^2, \ldots, x^n) }[/math] as the composite of [math]\displaystyle{ f }[/math] with the standard coordinates [math]\displaystyle{ x^1, x^2, \ldots, x^n }[/math] on [math]\displaystyle{ \mathbb{R}^n }[/math] (so that [math]\displaystyle{ x^j(p) }[/math] is the [math]\displaystyle{ j }[/math]-th component of [math]\displaystyle{ p\in\mathbb{R}^n }[/math]). Then the differentials [math]\displaystyle{ \left(dx^1\right)_p, \left(dx^2\right)_p, \ldots, \left(dx^n\right)_p }[/math] at a point [math]\displaystyle{ p }[/math] form a basis for the vector space of linear maps from [math]\displaystyle{ \mathbb{R}^n }[/math] to [math]\displaystyle{ \mathbb{R} }[/math] and therefore, if [math]\displaystyle{ f }[/math] is differentiable at [math]\displaystyle{ p }[/math], we can write [math]\displaystyle{ \operatorname{d}f_p }[/math] as a linear combination of these basis elements:

[math]\displaystyle{ df_p = \sum_{j=1}^n D_j f(p) \,(dx^j)_p. }[/math]

The coefficients [math]\displaystyle{ D_j f(p) }[/math] are (by definition) the partial derivatives of [math]\displaystyle{ f }[/math] at [math]\displaystyle{ p }[/math] with respect to [math]\displaystyle{ x^1, x^2, \ldots, x^n }[/math]. Hence, if [math]\displaystyle{ f }[/math] is differentiable on all of [math]\displaystyle{ \mathbb{R}^n }[/math], we can write, more concisely:

[math]\displaystyle{ \operatorname{d}f = \frac{\partial f}{\partial x^1} \,dx^1 + \frac{\partial f}{\partial x^2} \,dx^2 + \cdots +\frac{\partial f}{\partial x^n} \,dx^n. }[/math]

In the one-dimensional case this becomes

[math]\displaystyle{ df = \frac{df}{dx}dx }[/math]

as before.

This idea generalizes straightforwardly to functions from [math]\displaystyle{ \mathbb{R}^n }[/math] to [math]\displaystyle{ \mathbb{R}^m }[/math]. Furthermore, it has the decisive advantage over other definitions of the derivative that it is invariant under changes of coordinates. This means that the same idea can be used to define the differential of smooth maps between smooth manifolds.

Aside: Note that the existence of all the partial derivatives of [math]\displaystyle{ f(x) }[/math] at [math]\displaystyle{ x }[/math] is a necessary condition for the existence of a differential at [math]\displaystyle{ x }[/math]. However it is not a sufficient condition. For counterexamples, see Gateaux derivative.

Algebraic geometry

In algebraic geometry, differentials and other infinitesimal notions are handled in a very explicit way by accepting that the coordinate ring or structure sheaf of a space may contain nilpotent elements. The simplest example is the ring of dual numbers R[ε], where ε² = 0.

This can be motivated by the algebro-geometric point of view on the derivative of a function f from R to R at a point p. For this, note first that f − f(p) belongs to the ideal I_p of functions on R which vanish at p. If the derivative f vanishes at p, then f − f(p) belongs to the square I_p² of this ideal. Hence the derivative of f at p may be captured by the equivalence class [f − f(p)] in the quotient space I_p/I_p², and the 1-jet of f (which encodes its value and its first derivative) is the equivalence class of f in the space of all functions modulo I_p². Algebraic geometers regard this equivalence class as the restriction of f to a thickened version of the point p whose coordinate ring is not R (which is the quotient space of functions on R modulo I_p) but R[ε] which is the quotient space of functions on R modulo I_p². Such a thickened point is a simple example of a scheme.

Synthetic differential geometry

A third approach to infinitesimals is the method of synthetic differential geometry or smooth infinitesimal analysis. This is closely related to the algebraic-geometric approach, except that the infinitesimals are more implicit and intuitive. The main idea of this approach is to replace the category of sets with another category of smoothly varying sets which is a topos. In this category, one can define the real numbers, smooth functions, and so on, but the real numbers automatically contain nilpotent infinitesimals, so these do not need to be introduced by hand as in the algebraic geometric approach. However the logic in this new category is not identical to the familiar logic of the category of sets: in particular, the law of the excluded middle does not hold. This means that set-theoretic mathematical arguments only extend to smooth infinitesimal analysis if they are constructive (e.g., do not use proof by contradiction). Some regard this disadvantage as a positive thing, since it forces one to find constructive arguments wherever they are available.

Nonstandard analysis

The final approach to infinitesimals again involves extending the real numbers, but in a less drastic way. In the nonstandard analysis approach there are no nilpotent infinitesimals, only invertible ones, which may be viewed as the reciprocals of infinitely large numbers. Such extensions of the real numbers may be constructed explicitly using equivalence classes of sequences of real numbers, so that, for example, the sequence (1, 1/2, 1/3, ..., 1/n, ...) represents an infinitesimal. The first-order logic of this new set of hyperreal numbers is the same as the logic for the usual real numbers, but the completeness axiom (which involves second-order logic) does not hold. Nevertheless, this suffices to develop an elementary and quite intuitive approach to calculus using infinitesimals, see transfer principle.

See also

• Differential equation
• Differential form
• Differential of a function

References

• Apostol, Tom M. (1967), Calculus (2nd ed.), Wiley, ISBN 978-0-471-00005-1, https://archive.org/details/calculus01apos .
• Bell, John L. (1998), Invitation to Smooth Infinitesimal Analysis, http://publish.uwo.ca/~jbell/invitation%20to%20SIA.pdf .
• Boyer, Carl B. (1991), "Archimedes of Syracuse", A History of Mathematics (2nd ed.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8, https://archive.org/details/historyofmathema00boye .
• Darling, R. W. R. (1994), Differential forms and connections, Cambridge, UK: Cambridge University Press, ISBN 978-0-521-46800-8 .
• Eisenbud, David; Harris, Joe (1998), The Geometry of Schemes, Springer-Verlag, ISBN 978-0-387-98637-1 
• Keisler, H. Jerome (1986), Elementary Calculus: An Infinitesimal Approach (2nd ed.), http://www.math.wisc.edu/~keisler/calc.html .
• Kock, Anders (2006), Synthetic Differential Geometry (2nd ed.), Cambridge University Press, http://home.imf.au.dk/kock/sdg99.pdf .
• Lawvere, F.W. (1968), Outline of synthetic differential geometry (published 1998), http://www.acsu.buffalo.edu/~wlawvere/SDG_Outline.pdf .
• Moerdijk, I.; Reyes, G.E. (1991), Models for Smooth Infinitesimal Analysis, Springer-Verlag .
• Robinson, Abraham (1996), Non-standard analysis, Princeton University Press, ISBN 978-0-691-04490-3 .