Taylor's theorem

Short description: Approximation of a function by a truncated power series

The exponential function [math]\displaystyle{ y=e^x }[/math] (red) and the corresponding Taylor polynomial of degree four (dashed green) around the origin.

In calculus, Taylor's theorem gives an approximation of a [math]\displaystyle{ k }[/math]-times differentiable function around a given point by a polynomial of degree [math]\displaystyle{ k }[/math], called the [math]\displaystyle{ k }[/math]-th-order Taylor polynomial. For a smooth function, the Taylor polynomial is the truncation at the order [math]\displaystyle{ k }[/math] of the Taylor series of the function. The first-order Taylor polynomial is the linear approximation of the function, and the second-order Taylor polynomial is often referred to as the quadratic approximation. There are several versions of Taylor's theorem, some giving explicit estimates of the approximation error of the function by its Taylor polynomial.

Taylor's theorem is named after the mathematician Brook Taylor, who stated a version of it in 1715, although an earlier version of the result was already mentioned in 1671 by James Gregory.

Taylor's theorem is taught in introductory-level calculus courses and is one of the central elementary tools in mathematical analysis. It gives simple arithmetic formulas to accurately compute values of many transcendental functions such as the exponential function and trigonometric functions. It is the starting point of the study of analytic functions, and is fundamental in various areas of mathematics, as well as in numerical analysis and mathematical physics. Taylor's theorem also generalizes to multivariate and vector valued functions.

Motivation

Graph of [math]\displaystyle{ f(x)=e^x }[/math] (blue) with its linear approximation [math]\displaystyle{ P_1(x)=1+x }[/math] (red) at [math]\displaystyle{ a=0 }[/math].

If a real-valued function [math]\displaystyle{ f(x) }[/math] is differentiable at the point [math]\displaystyle{ x=a }[/math], then it has a linear approximation near this point. This means that there exists a function h₁(x) such that

[math]\displaystyle{ f(x) = f(a) + f'(a)(x - a) + h_1(x)(x - a), \quad \lim_{x \to a} h_1(x) = 0. }[/math]

Here

[math]\displaystyle{ P_1(x) = f(a) + f'(a)(x - a) }[/math]

is the linear approximation of [math]\displaystyle{ f(x) }[/math] for x near the point a, whose graph [math]\displaystyle{ y=P_1(x) }[/math] is the tangent line to the graph [math]\displaystyle{ y=f(x) }[/math] at x = a. The error in the approximation is: [math]\displaystyle{ R_1(x) = f(x) - P_1(x) = h_1(x)(x - a). }[/math]

As x tends to a, this error goes to zero much faster than [math]\displaystyle{ f'(a)(x{-}a) }[/math], making [math]\displaystyle{ f(x)\approx P_1(x) }[/math] a useful approximation.

Graph of [math]\displaystyle{ f(x)=e^x }[/math] (blue) with its quadratic approximation [math]\displaystyle{ P_2(x) = 1 +x + \dfrac{x^2}{2} }[/math] (red) at [math]\displaystyle{ a=0 }[/math]. Note the improvement in the approximation.

For a better approximation to [math]\displaystyle{ f(x) }[/math], we can fit a quadratic polynomial instead of a linear function:

[math]\displaystyle{ P_2(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2}(x - a)^2. }[/math]

Instead of just matching one derivative of [math]\displaystyle{ f(x) }[/math] at [math]\displaystyle{ x=a }[/math], this polynomial has the same first and second derivatives, as is evident upon differentiation.

Taylor's theorem ensures that the quadratic approximation is, in a sufficiently small neighborhood of [math]\displaystyle{ x=a }[/math], more accurate than the linear approximation. Specifically,

[math]\displaystyle{ f(x) = P_2(x) + h_2(x)(x - a)^2, \quad \lim_{x \to a} h_2(x) = 0. }[/math]

Here the error in the approximation is

[math]\displaystyle{ R_2(x) = f(x) - P_2(x) = h_2(x)(x - a)^2, }[/math]

which, given the limiting behavior of [math]\displaystyle{ h_2 }[/math], goes to zero faster than [math]\displaystyle{ (x - a)^2 }[/math] as x tends to a.

Approximation of [math]\displaystyle{ f(x)= \dfrac{1}{1+x^2} }[/math] (blue) by its Taylor polynomials [math]\displaystyle{ P_k }[/math] of order [math]\displaystyle{ k=1,\ldots,16 }[/math] centered at [math]\displaystyle{ x=0 }[/math] (red) and [math]\displaystyle{ x=1 }[/math] (green). The approximations do not improve at all outside [math]\displaystyle{ (-1,1) }[/math] and [math]\displaystyle{ (1-\sqrt{2}, 1+\sqrt{2}) }[/math], respectively.

Similarly, we might get still better approximations to f if we use polynomials of higher degree, since then we can match even more derivatives with f at the selected base point.

In general, the error in approximating a function by a polynomial of degree k will go to zero much faster than [math]\displaystyle{ (x-a)^k }[/math] as x tends to a. However, there are functions, even infinitely differentiable ones, for which increasing the degree of the approximating polynomial does not increase the accuracy of approximation: we say such a function fails to be analytic at x = a: it is not (locally) determined by its derivatives at this point.

Taylor's theorem is of asymptotic nature: it only tells us that the error [math]\displaystyle{ R_k }[/math] in an approximation by a [math]\displaystyle{ k }[/math]-th order Taylor polynomial P_k tends to zero faster than any nonzero [math]\displaystyle{ k }[/math]-th degree polynomial as [math]\displaystyle{ x \to a }[/math]. It does not tell us how large the error is in any concrete neighborhood of the center of expansion, but for this purpose there are explicit formulas for the remainder term (given below) which are valid under some additional regularity assumptions on f. These enhanced versions of Taylor's theorem typically lead to uniform estimates for the approximation error in a small neighborhood of the center of expansion, but the estimates do not necessarily hold for neighborhoods which are too large, even if the function f is analytic. In that situation one may have to select several Taylor polynomials with different centers of expansion to have reliable Taylor-approximations of the original function (see animation on the right.)

There are several ways we might use the remainder term:

1. Estimate the error for a polynomial P_k(x) of degree k estimating [math]\displaystyle{ f(x) }[/math] on a given interval (a – r, a + r). (Given the interval and degree, we find the error.)
2. Find the smallest degree k for which the polynomial P_k(x) approximates [math]\displaystyle{ f(x) }[/math] to within a given error tolerance on a given interval (a − r, a + r) . (Given the interval and error tolerance, we find the degree.)
3. Find the largest interval (a − r, a + r) on which P_k(x) approximates [math]\displaystyle{ f(x) }[/math] to within a given error tolerance. (Given the degree and error tolerance, we find the interval.)

Taylor's theorem in one real variable

Statement of the theorem

The precise statement of the most basic version of Taylor's theorem is as follows:

Theorem — Let k ≥ 1 be an integer and let the function f : R → R be k times differentiable at the point a ∈ R. Then there exists a function h_k : R → R such that

[math]\displaystyle{ f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(k)}(a)}{k!}(x-a)^k + h_k(x)(x-a)^k, }[/math] and [math]\displaystyle{ \lim_{x\to a} h_k(x) = 0. }[/math] This is called the Peano form of the remainder.

The polynomial appearing in Taylor's theorem is the [math]\displaystyle{ \boldsymbol{k} }[/math]-th order Taylor polynomial

[math]\displaystyle{ P_k(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(k)}(a)}{k!}(x-a)^k }[/math]

of the function f at the point a. The Taylor polynomial is the unique "asymptotic best fit" polynomial in the sense that if there exists a function h_k : R → R and a [math]\displaystyle{ k }[/math]-th order polynomial p such that

[math]\displaystyle{ f(x) = p(x) + h_k(x)(x-a)^k, \quad \lim_{x\to a} h_k(x) = 0 , }[/math]

then p = P_k. Taylor's theorem describes the asymptotic behavior of the remainder term

[math]\displaystyle{ R_k(x) = f(x) - P_k(x), }[/math]

which is the approximation error when approximating f with its Taylor polynomial. Using the little-o notation, the statement in Taylor's theorem reads as

[math]\displaystyle{ R_k(x) = o(|x-a|^{k}), \quad x\to a. }[/math]

Explicit formulas for the remainder

Under stronger regularity assumptions on f there are several precise formulas for the remainder term R_k of the Taylor polynomial, the most common ones being the following.

Mean-value forms of the remainder — Let f : R → R be k + 1 times differentiable on the open interval with f^(k) continuous on the closed interval between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math]. Then

[math]\displaystyle{ R_k(x) = \frac{f^{(k+1)}(\xi_L)}{(k+1)!} (x-a)^{k+1} }[/math]

for some real number [math]\displaystyle{ \xi_L }[/math] between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math]. This is the Lagrange form of the remainder.

Similarly,

[math]\displaystyle{ R_k(x) = \frac{f^{(k+1)}(\xi_C)}{k!}(x-\xi_C)^k(x-a) }[/math]

for some real number [math]\displaystyle{ \xi_C }[/math] between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math]. This is the Cauchy form of the remainder.

Both can be thought of as specific cases of the following result: Consider [math]\displaystyle{ p\gt 0 }[/math]

[math]\displaystyle{ R_k(x) = \frac{f^{(k+1)}(\xi_S)}{k!}(x-\xi_S)^{k+1-p}\frac{(x-a)^p}{p} }[/math] for some real number [math]\displaystyle{ \xi_S }[/math] between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math]. This is the Schlömilch form of the remainder (sometimes called the Schlömilch-Roché). The choice [math]\displaystyle{ p=k+1 }[/math] is the Lagrange form, whilst the choice [math]\displaystyle{ p=1 }[/math] is the Cauchy form.

These refinements of Taylor's theorem are usually proved using the mean value theorem, whence the name. Additionally, notice that this is precisely the mean value theorem when [math]\displaystyle{ k=0 }[/math]. Also other similar expressions can be found. For example, if G(t) is continuous on the closed interval and differentiable with a non-vanishing derivative on the open interval between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math], then

[math]\displaystyle{ R_k(x) = \frac{f^{(k+1)}(\xi)}{k!}(x-\xi)^k \frac{G(x)-G(a)}{G'(\xi)} }[/math]

for some number [math]\displaystyle{ \xi }[/math] between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math]. This version covers the Lagrange and Cauchy forms of the remainder as special cases, and is proved below using Cauchy's mean value theorem. The Lagrange form is obtained by taking [math]\displaystyle{ G(t)=(x-t)^{k+1} }[/math] and the Cauchy form is obtained by taking [math]\displaystyle{ G(t)=t-a }[/math].

The statement for the integral form of the remainder is more advanced than the previous ones, and requires understanding of Lebesgue integration theory for the full generality. However, it holds also in the sense of Riemann integral provided the (k + 1)th derivative of f is continuous on the closed interval [a,x].

Integral form of the remainder — Let [math]\displaystyle{ f^{(k)} }[/math] be absolutely continuous on the closed interval between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math]. Then

[math]\displaystyle{ R_k(x) = \int_a^x \frac{f^{(k+1)} (t)}{k!} (x - t)^k \, dt. }[/math]

Due to absolute continuity of f^(k) on the closed interval between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math], its derivative f^(k+1) exists as an L¹-function, and the result can be proven by a formal calculation using fundamental theorem of calculus and integration by parts.

Estimates for the remainder

It is often useful in practice to be able to estimate the remainder term appearing in the Taylor approximation, rather than having an exact formula for it. Suppose that f is (k + 1)-times continuously differentiable in an interval I containing a. Suppose that there are real constants q and Q such that

[math]\displaystyle{ q\le f^{(k+1)}(x)\le Q }[/math]

throughout I. Then the remainder term satisfies the inequality

[math]\displaystyle{ q\frac{(x-a)^{k+1}}{(k+1)!}\le R_k(x)\le Q\frac{(x-a)^{k+1}}{(k+1)!}, }[/math]

if x > a, and a similar estimate if x < a. This is a simple consequence of the Lagrange form of the remainder. In particular, if

[math]\displaystyle{ |f^{(k+1)}(x)|\le M }[/math]

on an interval I = (a − r,a + r) with some [math]\displaystyle{ r \gt 0 }[/math] , then

[math]\displaystyle{ |R_k(x)|\le M\frac{|x-a|^{k+1}}{(k+1)!}\le M\frac{r^{k+1}}{(k+1)!} }[/math]

for all x∈(a − r,a + r). The second inequality is called a uniform estimate, because it holds uniformly for all x on the interval (a − r,a + r).

Example

Approximation of [math]\displaystyle{ e^x }[/math] (blue) by its Taylor polynomials [math]\displaystyle{ P_k }[/math] of order [math]\displaystyle{ k=1,\ldots,7 }[/math] centered at [math]\displaystyle{ x=0 }[/math] (red).

Suppose that we wish to find the approximate value of the function [math]\displaystyle{ f(x)=e^x }[/math] on the interval [math]\displaystyle{ [-1,1] }[/math] while ensuring that the error in the approximation is no more than 10⁻⁵. In this example we pretend that we only know the following properties of the exponential function:

[math]\displaystyle{ e^0=1, \qquad \frac{d}{dx} e^x = e^x, \qquad e^x\gt 0, \qquad x\in\R. }[/math]

(★)

From these properties it follows that [math]\displaystyle{ f^{(k)}(x)=e^x }[/math] for all [math]\displaystyle{ k }[/math], and in particular, [math]\displaystyle{ f^{(k)}(0)=1 }[/math]. Hence the [math]\displaystyle{ k }[/math]-th order Taylor polynomial of [math]\displaystyle{ f }[/math] at [math]\displaystyle{ 0 }[/math] and its remainder term in the Lagrange form are given by

[math]\displaystyle{ P_k(x) = 1+x+\frac{x^2}{2!}+\cdots+\frac{x^k}{k!}, \qquad R_k(x)=\frac{e^\xi}{(k+1)!}x^{k+1}, }[/math]

where [math]\displaystyle{ \xi }[/math] is some number between 0 and x. Since e^x is increasing by (★), we can simply use [math]\displaystyle{ e^x \leq 1 }[/math] for [math]\displaystyle{ x \in [-1,0] }[/math] to estimate the remainder on the subinterval [math]\displaystyle{ [-1,0] }[/math]. To obtain an upper bound for the remainder on [math]\displaystyle{ [0,1] }[/math], we use the property [math]\displaystyle{ e^\xi \lt e^x }[/math] for [math]\displaystyle{ 0\lt \xi\lt x }[/math] to estimate

[math]\displaystyle{ e^x = 1 + x + \frac{e^\xi}{2}x^2 \lt 1 + x + \frac{e^x}{2}x^2, \qquad 0 \lt x\leq 1 }[/math]

using the second order Taylor expansion. Then we solve for e^x to deduce that

[math]\displaystyle{ e^x \leq \frac{1+x}{1-\frac{x^2}{2}} = 2\frac{1+x}{2-x^2} \leq 4, \qquad 0 \leq x\leq 1 }[/math]

simply by maximizing the numerator and minimizing the denominator. Combining these estimates for e^x we see that

[math]\displaystyle{ |R_k(x)| \leq \frac{4|x|^{k+1}}{(k+1)!} \leq \frac{4}{(k+1)!}, \qquad -1\leq x \leq 1, }[/math]

so the required precision is certainly reached, when

[math]\displaystyle{ \frac{4}{(k+1)!} \lt 10^{-5} \quad \Longleftrightarrow \quad 4\cdot 10^5 \lt (k+1)! \quad \Longleftrightarrow \quad k \geq 9. }[/math]

(See factorial or compute by hand the values [math]\displaystyle{ 9! =362880 }[/math] and [math]\displaystyle{ 10! =3628800 }[/math].) As a conclusion, Taylor's theorem leads to the approximation

[math]\displaystyle{ e^x = 1+x+\frac{x^2}{2!} + \cdots + \frac{x^9}{9!} + R_9(x), \qquad |R_9(x)| \lt 10^{-5}, \qquad -1\leq x \leq 1. }[/math]

For instance, this approximation provides a decimal expression [math]\displaystyle{ e \approx 2.71828 }[/math], correct up to five decimal places.

Relationship to analyticity

Taylor expansions of real analytic functions

Let I ⊂ R be an open interval. By definition, a function f : I → R is real analytic if it is locally defined by a convergent power series. This means that for every a ∈ I there exists some r > 0 and a sequence of coefficients c_k ∈ R such that (a − r, a + r) ⊂ I and

[math]\displaystyle{ f(x) = \sum_{k=0}^\infty c_k(x-a)^k = c_0 + c_1(x-a) + c_2(x-a)^2 + \cdots, \qquad |x-a|\lt r. }[/math]

In general, the radius of convergence of a power series can be computed from the Cauchy–Hadamard formula

[math]\displaystyle{ \frac{1}{R} = \limsup_{k\to\infty}|c_k|^\frac{1}{k}. }[/math]

This result is based on comparison with a geometric series, and the same method shows that if the power series based on a converges for some b ∈ R, it must converge uniformly on the closed interval [math]\displaystyle{ [a-r_b,a+r_b] }[/math], where [math]\displaystyle{ r_b=\left\vert b-a \right\vert }[/math]. Here only the convergence of the power series is considered, and it might well be that (a − R,a + R) extends beyond the domain I of f.

The Taylor polynomials of the real analytic function f at a are simply the finite truncations

[math]\displaystyle{ P_k(x) = \sum_{j=0}^k c_j(x-a)^j, \qquad c_j = \frac{f^{(j)}(a)}{j!} }[/math]

of its locally defining power series, and the corresponding remainder terms are locally given by the analytic functions

[math]\displaystyle{ R_k(x) = \sum_{j=k+1}^\infty c_j(x-a)^j = (x-a)^k h_k(x), \qquad |x-a|\lt r. }[/math]

Here the functions

[math]\displaystyle{ \begin{align} & h_k:(a-r,a+r)\to \R \\[1ex] & h_k(x) = (x-a)\sum_{j=0}^\infty c_{k+1+j} \left(x - a\right)^j \end{align} }[/math]

are also analytic, since their defining power series have the same radius of convergence as the original series. Assuming that [a − r, a + r] ⊂ I and r < R, all these series converge uniformly on (a − r, a + r). Naturally, in the case of analytic functions one can estimate the remainder term [math]\displaystyle{ R_k(x) }[/math] by the tail of the sequence of the derivatives f′(a) at the center of the expansion, but using complex analysis also another possibility arises, which is described below.

Taylor's theorem and convergence of Taylor series

The Taylor series of f will converge in some interval in which all its derivatives are bounded and do not grow too fast as k goes to infinity. (However, even if the Taylor series converges, it might not converge to f, as explained below; f is then said to be non-analytic.)

One might think of the Taylor series

[math]\displaystyle{ f(x) \approx \sum_{k=0}^\infty c_k(x-a)^k = c_0 + c_1(x-a) + c_2(x-a)^2 + \cdots }[/math]

of an infinitely many times differentiable function f : R → R as its "infinite order Taylor polynomial" at a. Now the estimates for the remainder imply that if, for any r, the derivatives of f are known to be bounded over (a − r, a + r), then for any order k and for any r > 0 there exists a constant M_k,r > 0 such that

[math]\displaystyle{ |R_k(x)| \leq M_{k,r} \frac{|x-a|^{k+1}}{(k+1)!} }[/math]

(★★)

for every x ∈ (a − r,a + r). Sometimes the constants M_k,r can be chosen in such way that M_k,r is bounded above, for fixed r and all k. Then the Taylor series of f converges uniformly to some analytic function

[math]\displaystyle{ \begin{align} & T_f:(a-r,a+r)\to\R \\ & T_f(x) = \sum_{k=0}^\infty \frac{f^{(k)}(a)}{k!} \left(x-a\right)^k \end{align} }[/math]

(One also gets convergence even if M_k,r is not bounded above as long as it grows slowly enough.)

The limit function T_f is by definition always analytic, but it is not necessarily equal to the original function f, even if f is infinitely differentiable. In this case, we say f is a non-analytic smooth function, for example a flat function:

[math]\displaystyle{ \begin{align} & f:\R \to \R \\ & f(x) = \begin{cases} e^{-\frac{1}{x^2}} & x\gt 0 \\ 0 & x \leq 0 . \end{cases} \end{align} }[/math]

Using the chain rule repeatedly by mathematical induction, one shows that for any order k,

[math]\displaystyle{ f^{(k)}(x) = \begin{cases} \frac{p_k(x)}{x^{3k}}\cdot e^{-\frac{1}{x^2}} & x\gt 0 \\ 0 & x \leq 0 \end{cases} }[/math]

for some polynomial p_k of degree 2(k − 1). The function [math]\displaystyle{ e^{-\frac{1}{x^2}} }[/math] tends to zero faster than any polynomial as [math]\displaystyle{ x \to 0 }[/math], so f is infinitely many times differentiable and f^(k)(0) = 0 for every positive integer k. The above results all hold in this case:

• The Taylor series of f converges uniformly to the zero function T_f(x) = 0, which is analytic with all coefficients equal to zero.
• The function f is unequal to this Taylor series, and hence non-analytic.
• For any order k ∈ N and radius r > 0 there exists M_k,r > 0 satisfying the remainder bound (★★) above.

However, as k increases for fixed r, the value of M_k,r grows more quickly than r^k, and the error does not go to zero.

Taylor's theorem in complex analysis

Taylor's theorem generalizes to functions f : C → C which are complex differentiable in an open subset U ⊂ C of the complex plane. However, its usefulness is dwarfed by other general theorems in complex analysis. Namely, stronger versions of related results can be deduced for complex differentiable functions f : U → C using Cauchy's integral formula as follows.

Let r > 0 such that the closed disk B(z, r) ∪ S(z, r) is contained in U. Then Cauchy's integral formula with a positive parametrization γ(t) = z + re^it of the circle S(z, r) with [math]\displaystyle{ t \in [0,2 \pi] }[/math] gives

[math]\displaystyle{ f(z) = \frac{1}{2\pi i}\int_\gamma \frac{f(w)}{w-z}\,dw, \quad f'(z) = \frac{1}{2\pi i}\int_\gamma \frac{f(w)}{(w-z)^2} \, dw, \quad \ldots, \quad f^{(k)}(z) = \frac{k!}{2\pi i}\int_\gamma \frac{f(w)}{(w-z)^{k+1}} \, dw. }[/math]

Here all the integrands are continuous on the circle S(z, r), which justifies differentiation under the integral sign. In particular, if f is once complex differentiable on the open set U, then it is actually infinitely many times complex differentiable on U. One also obtains the Cauchy's estimates

[math]\displaystyle{ |f^{(k)}(z)| \leq \frac{k!}{2\pi}\int_\gamma \frac{M_r}{|w-z|^{k+1}} \, dw = \frac{k!M_r}{r^k}, \quad M_r = \max_{|w-c|=r}|f(w)| }[/math]

for any z ∈ U and r > 0 such that B(z, r) ∪ S(c, r) ⊂ U. These estimates imply that the complex Taylor series

[math]\displaystyle{ T_f(z) = \sum_{k=0}^\infty \frac{f^{(k)}(c)}{k!}(z-c)^k }[/math]

of f converges uniformly on any open disk [math]\displaystyle{ B(c,r) \subset U }[/math] with [math]\displaystyle{ S(c,r) \subset U }[/math] into some function T_f. Furthermore, using the contour integral formulas for the derivatives f^(k)(c),

[math]\displaystyle{ \begin{align} T_f(z) &= \sum_{k=0}^\infty \frac{(z-c)^k}{2\pi i}\int_\gamma \frac{f(w)}{(w-c)^{k+1}} \, dw \\ &= \frac{1}{2\pi i} \int_\gamma \frac{f(w)}{w-c} \sum_{k=0}^\infty \left(\frac{z-c}{w-c}\right)^k \, dw \\ &= \frac{1}{2\pi i} \int_\gamma \frac{f(w)}{w-c}\left( \frac{1}{1-\frac{z-c}{w-c}} \right) \, dw \\ &= \frac{1}{2\pi i} \int_\gamma \frac{f(w)}{w-z} \, dw = f(z), \end{align} }[/math]

so any complex differentiable function f in an open set U ⊂ C is in fact complex analytic. All that is said for real analytic functions here holds also for complex analytic functions with the open interval I replaced by an open subset U ∈ C and a-centered intervals (a − r, a + r) replaced by c-centered disks B(c, r). In particular, the Taylor expansion holds in the form

[math]\displaystyle{ f(z) = P_k(z) + R_k(z), \quad P_k(z) = \sum_{j=0}^k \frac{f^{(j)}(c)}{j!}(z-c)^j, }[/math]

where the remainder term R_k is complex analytic. Methods of complex analysis provide some powerful results regarding Taylor expansions. For example, using Cauchy's integral formula for any positively oriented Jordan curve [math]\displaystyle{ \gamma }[/math] which parametrizes the boundary [math]\displaystyle{ \partial W \subset U }[/math] of a region [math]\displaystyle{ W \subset U }[/math], one obtains expressions for the derivatives f^(j)(c) as above, and modifying slightly the computation for T_f(z) = f(z), one arrives at the exact formula

[math]\displaystyle{ R_k(z) = \sum_{j=k+1}^\infty \frac{(z-c)^j}{2\pi i} \int_\gamma \frac{f(w)}{(w-c)^{j+1}} \, dw = \frac{(z-c)^{k+1}}{2\pi i} \int_\gamma \frac{f(w) \, dw}{(w-c)^{k+1}(w-z)} , \qquad z\in W. }[/math]

The important feature here is that the quality of the approximation by a Taylor polynomial on the region [math]\displaystyle{ W \subset U }[/math] is dominated by the values of the function f itself on the boundary [math]\displaystyle{ \partial W \subset U }[/math]. Similarly, applying Cauchy's estimates to the series expression for the remainder, one obtains the uniform estimates

[math]\displaystyle{ |R_k(z)| \leq \sum_{j=k+1}^\infty \frac{M_r |z-c|^j}{r^j} = \frac{M_r}{r^{k+1}} \frac{|z-c|^{k+1}}{1-\frac{|z-c|}{r}} \leq \frac{M_r \beta^{k+1}}{1-\beta}, \qquad \frac{|z-c|}{r} \leq \beta \lt 1. }[/math]

Example

Complex plot of [math]\displaystyle{ f(z)=\frac{1}{1+z^2} }[/math]. Modulus is shown by elevation and argument by coloring: cyan = [math]\displaystyle{ 0 }[/math], blue = [math]\displaystyle{ \frac{\pi}{3} }[/math], violet = [math]\displaystyle{ \frac{2\pi}{3} }[/math], red = [math]\displaystyle{ \pi }[/math], yellow = [math]\displaystyle{ \frac{4\pi}{3} }[/math], green = [math]\displaystyle{ \frac{5\pi}{3} }[/math].

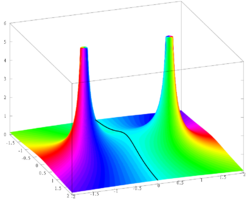
The function

[math]\displaystyle{ \begin{align} & f : \R \to \R \\ & f(x) = \frac{1}{1+x^2} \end{align} }[/math]

is real analytic, that is, locally determined by its Taylor series. This function was plotted above to illustrate the fact that some elementary functions cannot be approximated by Taylor polynomials in neighborhoods of the center of expansion which are too large. This kind of behavior is easily understood in the framework of complex analysis. Namely, the function f extends into a meromorphic function

[math]\displaystyle{ \begin{align} & f:\Complex \cup \{\infty\} \to \Complex \cup \{\infty\} \\ & f(z) = \frac{1}{1+z^2} \end{align} }[/math]

on the compactified complex plane. It has simple poles at [math]\displaystyle{ z=i }[/math] and [math]\displaystyle{ z=-i }[/math], and it is analytic elsewhere. Now its Taylor series centered at z₀ converges on any disc B(z₀, r) with r < |z − z₀|, where the same Taylor series converges at z ∈ C. Therefore, Taylor series of f centered at 0 converges on B(0, 1) and it does not converge for any z ∈ C with |z| > 1 due to the poles at i and −i. For the same reason the Taylor series of f centered at 1 converges on [math]\displaystyle{ B(1, \sqrt{2}) }[/math] and does not converge for any z ∈ C with [math]\displaystyle{ \left\vert z-1 \right\vert\gt \sqrt{2} }[/math].

Generalizations of Taylor's theorem

Higher-order differentiability

A function f: Rⁿ → R is differentiable at a ∈ Rⁿ if and only if there exists a linear functional L : Rⁿ → R and a function h : Rⁿ → R such that

[math]\displaystyle{ f(\boldsymbol{x}) = f(\boldsymbol{a}) + L(\boldsymbol{x}-\boldsymbol{a}) + h(\boldsymbol{x})\lVert\boldsymbol{x}-\boldsymbol{a}\rVert, \qquad \lim_{\boldsymbol{x}\to\boldsymbol{a}} h(\boldsymbol{x})=0. }[/math]

If this is the case, then [math]\displaystyle{ L = df(\boldsymbol{a}) }[/math] is the (uniquely defined) differential of f at the point a. Furthermore, then the partial derivatives of f exist at a and the differential of f at a is given by

[math]\displaystyle{ df( \boldsymbol{a} )( \boldsymbol{v} ) = \frac{\partial f}{\partial x_1}(\boldsymbol{a}) v_1 + \cdots + \frac{\partial f}{\partial x_n}(\boldsymbol{a}) v_n. }[/math]

Introduce the multi-index notation

[math]\displaystyle{ |\alpha| = \alpha_1+\cdots+\alpha_n, \quad \alpha!=\alpha_1!\cdots\alpha_n!, \quad \boldsymbol{x}^\alpha=x_1^{\alpha_1}\cdots x_n^{\alpha_n} }[/math]

for α ∈ Nⁿ and x ∈ Rⁿ. If all the [math]\displaystyle{ k }[/math]-th order partial derivatives of f : Rⁿ → R are continuous at a ∈ Rⁿ, then by Clairaut's theorem, one can change the order of mixed derivatives at a, so the notation

[math]\displaystyle{ D^\alpha f = \frac{\partial^{|\alpha|}f}{\partial x_1^{\alpha_1}\cdots \partial x_n^{\alpha_n}}, \qquad |\alpha|\leq k }[/math]

for the higher order partial derivatives is justified in this situation. The same is true if all the (k − 1)-th order partial derivatives of f exist in some neighborhood of a and are differentiable at a. Then we say that f is k times differentiable at the point a.

Taylor's theorem for multivariate functions

Using notations of the preceding section, one has the following theorem.

Multivariate version of Taylor's theorem — Let f : Rⁿ → R be a k-times continuously differentiable function at the point a ∈ Rⁿ. Then there exist functions h_α : Rⁿ → R, where [math]\displaystyle{ |\alpha|=k, }[/math] such that

[math]\displaystyle{ \begin{align} & f(\boldsymbol{x}) = \sum_{|\alpha|\leq k} \frac{D^\alpha f(\boldsymbol{a})}{\alpha!} (\boldsymbol{x}-\boldsymbol{a})^\alpha + \sum_{|\alpha|=k} h_\alpha(\boldsymbol{x})(\boldsymbol{x}-\boldsymbol{a})^\alpha, \\ & \mbox{and}\quad \lim_{\boldsymbol{x}\to \boldsymbol{a}}h_\alpha(\boldsymbol{x})=0. \end{align} }[/math]

If the function f : Rⁿ → R is k + 1 times continuously differentiable in a closed ball [math]\displaystyle{ B = \{ \mathbf{y} \in \R^n : \left\|\mathbf{a}-\mathbf{y}\right\| \leq r\} }[/math] for some [math]\displaystyle{ r \gt 0 }[/math], then one can derive an exact formula for the remainder in terms of (k+1)-th order partial derivatives of f in this neighborhood. Namely,

[math]\displaystyle{ \begin{align} & f( \boldsymbol{x} ) = \sum_{|\alpha|\leq k} \frac{D^\alpha f(\boldsymbol{a})}{\alpha!} (\boldsymbol{x}-\boldsymbol{a})^\alpha + \sum_{|\beta|=k+1} R_\beta(\boldsymbol{x})(\boldsymbol{x}-\boldsymbol{a})^\beta, \\ & R_\beta( \boldsymbol{x} ) = \frac{|\beta|}{\beta!} \int_0^1 (1-t)^{|\beta|-1}D^\beta f \big(\boldsymbol{a}+t( \boldsymbol{x}-\boldsymbol{a} )\big) \, dt. \end{align} }[/math]

In this case, due to the continuity of (k+1)-th order partial derivatives in the compact set B, one immediately obtains the uniform estimates

[math]\displaystyle{ \left|R_\beta(\boldsymbol{x})\right| \leq \frac{1}{\beta!} \max_{|\alpha|=|\beta|} \max_{\boldsymbol{y}\in B} |D^\alpha f(\boldsymbol{y})|, \qquad \boldsymbol{x}\in B. }[/math]

Example in two dimensions

For example, the third-order Taylor polynomial of a smooth function [math]\displaystyle{ f:\mathbb R^2\to\mathbb R }[/math] is, denoting [math]\displaystyle{ \boldsymbol{x}-\boldsymbol{a}=\boldsymbol{v} }[/math],

[math]\displaystyle{ \begin{align} P_3(\boldsymbol{x}) = f ( \boldsymbol{a} ) + {} &\frac{\partial f}{\partial x_1}( \boldsymbol{a} ) v_1 + \frac{\partial f}{\partial x_2}( \boldsymbol{a} ) v_2 + \frac{\partial^2 f}{\partial x_1^2}( \boldsymbol{a} ) \frac {v_1^2}{2!} + \frac{\partial^2 f}{\partial x_1 \partial x_2}( \boldsymbol{a} ) v_1 v_2 + \frac{\partial^2 f}{\partial x_2^2}( \boldsymbol{a} ) \frac{v_2^2}{2!} \\ & + \frac{\partial^3 f}{\partial x_1^3}( \boldsymbol{a} ) \frac{v_1^3}{3!} + \frac{\partial^3 f}{\partial x_1^2 \partial x_2}( \boldsymbol{a} ) \frac{v_1^2 v_2}{2!} + \frac{\partial^3 f}{\partial x_1 \partial x_2^2}( \boldsymbol{a} ) \frac{v_1 v_2^2}{2!} + \frac{\partial^3 f}{\partial x_2^3}( \boldsymbol{a} ) \frac{v_2^3}{3!} \end{align} }[/math]

Proofs

Proof for Taylor's theorem in one real variable

Let

[math]\displaystyle{ h_k(x) = \begin{cases} \frac{f(x) - P(x)}{(x-a)^k} & x\not=a\\ 0&x=a \end{cases} }[/math]

where, as in the statement of Taylor's theorem,

[math]\displaystyle{ P(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(k)}(a)}{k!}(x-a)^k. }[/math]

It is sufficient to show that

[math]\displaystyle{ \lim_{x\to a} h_k(x) =0. }[/math]

The proof here is based on repeated application of L'Hôpital's rule. Note that, for each [math]\displaystyle{ j=0,1,...,k-1 }[/math], [math]\displaystyle{ f^{(j)}(a)=P^{(j)}(a) }[/math]. Hence each of the first [math]\displaystyle{ k-1 }[/math] derivatives of the numerator in [math]\displaystyle{ h_k(x) }[/math] vanishes at [math]\displaystyle{ x=a }[/math], and the same is true of the denominator. Also, since the condition that the function [math]\displaystyle{ f }[/math] be [math]\displaystyle{ k }[/math] times differentiable at a point requires differentiability up to order [math]\displaystyle{ k-1 }[/math] in a neighborhood of said point (this is true, because differentiability requires a function to be defined in a whole neighborhood of a point), the numerator and its [math]\displaystyle{ k-2 }[/math] derivatives are differentiable in a neighborhood of [math]\displaystyle{ a }[/math]. Clearly, the denominator also satisfies said condition, and additionally, doesn't vanish unless [math]\displaystyle{ x=a }[/math], therefore all conditions necessary for L'Hôpital's rule are fulfilled, and its use is justified. So

[math]\displaystyle{ \begin{align} \lim_{x\to a} \frac{f(x) - P(x)}{(x-a)^k} &= \lim_{x\to a} \frac{\frac{d}{dx}(f(x) - P(x))}{\frac{d}{dx}(x-a)^k} \\[1ex] &= \cdots \\[1ex] &= \lim_{x\to a} \frac{\frac{d^{k-1}}{dx^{k-1}}(f(x) - P(x))}{\frac{d^{k-1}}{dx^{k-1}}(x-a)^k}\\[1ex] &= \frac{1}{k!}\lim_{x\to a} \frac{f^{(k-1)}(x) - P^{(k-1)}(x)}{x-a}\\[1ex] &=\frac{1}{k!}(f^{(k)}(a) - P^{(k)}(a)) = 0 \end{align} }[/math]

where the second-to-last equality follows by the definition of the derivative at [math]\displaystyle{ x=a }[/math].

Alternate proof for Taylor's theorem in one real variable

Let [math]\displaystyle{ f(x) }[/math] be any real-valued continuous function to be approximated by the Taylor polynomial.

Step 1: Let [math]\displaystyle{ F }[/math] and [math]\displaystyle{ G }[/math] be functions. Set [math]\displaystyle{ F }[/math] and [math]\displaystyle{ G }[/math] to be

[math]\displaystyle{ \begin{align} F(x) = f(x) - \sum^{n-1}_{k=0} \frac{f^{(k)}(a)}{k!}(x-a)^{k} \end{align} }[/math]

[math]\displaystyle{ \begin{align} G(x) = (x-a)^{n} \end{align} }[/math]

Step 2: Properties of [math]\displaystyle{ F }[/math] and [math]\displaystyle{ G }[/math]:

[math]\displaystyle{ \begin{align} F(a) & = f(a) - f(a) - f'(a)(a - a) - ... - \frac{f^{(n-1)}(a)(a-a)^{n-1}}{(n-1)!} = 0 \\ G(a) & = (a-a)^n = 0 \end{align} }[/math]

Similarly,

[math]\displaystyle{ \begin{align} F'(a) = f'(a) - f'(a) - \frac{2f''(a)(a-a)}{1!} - ... - \frac{f^{(n-2)}(a)(n-1)(a-a)^{n-2}}{(n-1)!} = 0 \end{align} }[/math]

[math]\displaystyle{ \begin{align} G'(a) &= n(a-a)^{n-1} = 0\\ &\qquad \vdots\\ G^{(n-1)}(a) &= F^{(n-1)}(a) = 0 \end{align} }[/math]

Step 3: Use Cauchy Mean Value Theorem

Let [math]\displaystyle{ f_{1} }[/math] and [math]\displaystyle{ g_{1} }[/math] be continuous functions on [math]\displaystyle{ [a, b] }[/math]. Since [math]\displaystyle{ a \lt x \lt b }[/math] so we can work with the interval [math]\displaystyle{ [a, x] }[/math]. Let [math]\displaystyle{ f_{1} }[/math] and [math]\displaystyle{ g_{1} }[/math] be differentiable on [math]\displaystyle{ (a, x) }[/math]. Assume [math]\displaystyle{ g_{1}'(x) \neq 0 }[/math] for all [math]\displaystyle{ x \in (a, b) }[/math]. Then there exists [math]\displaystyle{ c_{1} \in (a, x) }[/math] such that

[math]\displaystyle{ \begin{align} \frac{f_{1}(x) - f_{1}(a)}{g_{1}(x) - g_{1}(a)} = \frac{f_{1}'(c_{1})}{g_{1}'(c_{1})} \end{align} }[/math]

Note: [math]\displaystyle{ G'(x) \neq 0 }[/math] in [math]\displaystyle{ (a, b) }[/math] and [math]\displaystyle{ F(a), G(a) = 0 }[/math] so

[math]\displaystyle{ \begin{align} \frac{F(x)}{G(x)} = \frac{F(x) - F(a)}{G(x) - G(a)} = \frac{F'(c_{1})}{G'(c_{1})} \end{align} }[/math]

for some [math]\displaystyle{ c_{1} \in (a, x) }[/math].

This can also be performed for [math]\displaystyle{ (a, c_{1}) }[/math]:

[math]\displaystyle{ \begin{align} \frac{F'(c_{1})}{G'(c_{1})} = \frac{F'(c_{1}) - F'(a)}{G'(c_{1}) - G'(a)} = \frac{F''(c_{2})}{G''(c_{2})} \end{align} }[/math]

for some [math]\displaystyle{ c_{2} \in (a, c_{1}) }[/math]. This can be continued to [math]\displaystyle{ c_{n} }[/math].

This gives a partition in [math]\displaystyle{ (a, b) }[/math]:

[math]\displaystyle{ a \lt c_{n} \lt c_{n-1} \lt \dots \lt c_{1} \lt x }[/math]

with

[math]\displaystyle{ \frac{F(x)}{G(x)} = \frac{F'(c_{1})}{G'(c_{1})} = \dots = \frac{F^{(n)}(c_{n})}{G^{(n)}(c_{n})} . }[/math]

Set [math]\displaystyle{ c = c_{n} }[/math]:

[math]\displaystyle{ \frac{F(x)}{G(x)} = \frac{F^{(n)}(c)}{G^{(n)}(c)} }[/math]

Step 4: Substitute back

[math]\displaystyle{ \begin{align} \frac{F(x)}{G(x)} = \frac{f(x) - \sum^{n-1}_{k=0} \frac{f^{(k)}(a)}{k!}(x-a)^{k}}{(x-a)^{n}} = \frac{F^{(n)}(c)}{G^{(n)}(c)} \end{align} }[/math]

By the Power Rule, repeated derivatives of [math]\displaystyle{ (x - a)^{n} }[/math], [math]\displaystyle{ G^{(n)}(c) = n(n-1)...1 }[/math], so:

[math]\displaystyle{ \frac{F^{(n)}(c)}{G^{(n)}(c)} = \frac{f^{(n)}(c)}{n(n-1)\cdots1} = \frac{f^{(n)}(c)}{n!}. }[/math]

This leads to:

[math]\displaystyle{ \begin{align} f(x) - \sum^{n-1}_{k=0} \frac{f^{(k)}(a)}{k!}(x-a)^{k} = \frac{f^{(n)}(c)}{n!}(x-a)^{n} \end{align}. }[/math]

By rearranging, we get:

[math]\displaystyle{ \begin{align} f(x) = \sum^{n-1}_{k=0} \frac{f^{(k)}(a)}{k!}(x-a)^{k} + \frac{f^{(n)}(c)}{n!}(x-a)^{n} \end{align}, }[/math]

or because [math]\displaystyle{ c_{n} = a }[/math] eventually:

[math]\displaystyle{ f(x) = \sum^{n}_{k=0} \frac{f^{(k)}(a)}{k!}(x-a)^{k}. }[/math]

Derivation for the mean value forms of the remainder

Let G be any real-valued function, continuous on the closed interval between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math] and differentiable with a non-vanishing derivative on the open interval between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math], and define

[math]\displaystyle{ F(t) = f(t) + f'(t)(x-t) + \frac{f''(t)}{2!}(x-t)^2 + \cdots + \frac{f^{(k)}(t)}{k!}(x-t)^k. }[/math]

For [math]\displaystyle{ t \in [a,x] }[/math]. Then, by Cauchy's mean value theorem,

[math]\displaystyle{ \frac{F'(\xi)}{G'(\xi)} = \frac{F(x) - F(a)}{G(x) - G(a)} }[/math]

(★★★)

for some [math]\displaystyle{ \xi }[/math] on the open interval between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math]. Note that here the numerator [math]\displaystyle{ F(x)-F(a)=R_k(x) }[/math] is exactly the remainder of the Taylor polynomial for [math]\displaystyle{ y=f(x) }[/math]. Compute

[math]\displaystyle{ \begin{align} F'(t) = {} & f'(t) + \big(f''(t)(x-t) - f'(t)\big) + \left(\frac{f^{(3)}(t)}{2!}(x-t)^2 - \frac{f^{(2)}(t)}{1!}(x-t)\right) + \cdots \\ & \cdots + \left( \frac{f^{(k+1)}(t)}{k!}(x-t)^k - \frac{f^{(k)}(t)}{(k-1)!}(x-t)^{k-1}\right) = \frac{f^{(k+1)}(t)}{k!}(x-t)^k, \end{align} }[/math]

plug it into (★★★) and rearrange terms to find that

[math]\displaystyle{ R_k(x) = \frac{f^{(k+1)}(\xi)}{k!}(x-\xi)^k \frac{G(x)-G(a)}{G'(\xi)}. }[/math]

This is the form of the remainder term mentioned after the actual statement of Taylor's theorem with remainder in the mean value form. The Lagrange form of the remainder is found by choosing [math]\displaystyle{ G(t) = (x-t)^{k+1} }[/math] and the Cauchy form by choosing [math]\displaystyle{ G(t) = t-a }[/math].

Remark. Using this method one can also recover the integral form of the remainder by choosing

[math]\displaystyle{ G(t) = \int_a^t \frac{f^{(k+1)}(s)}{k!} (x-s)^k \, ds, }[/math]

but the requirements for f needed for the use of mean value theorem are too strong, if one aims to prove the claim in the case that f^(k) is only absolutely continuous. However, if one uses Riemann integral instead of Lebesgue integral, the assumptions cannot be weakened.

Derivation for the integral form of the remainder

Due to absolute continuity of [math]\displaystyle{ f^{(k)} }[/math] on the closed interval between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math] its derivative [math]\displaystyle{ f^{(k+1)} }[/math] exists as an [math]\displaystyle{ L^1 }[/math]-function, and we can use fundamental theorem of calculus and integration by parts. This same proof applies for the Riemann integral assuming that [math]\displaystyle{ f^{(k)} }[/math] is continuous on the closed interval and differentiable on the open interval between [math]\displaystyle{ a }[/math] and [math]\displaystyle{ x }[/math], and this leads to the same result than using the mean value theorem.

The fundamental theorem of calculus states that

[math]\displaystyle{ f(x)=f(a)+ \int_a^x \, f'(t) \, dt. }[/math]

Now we can integrate by parts and use the fundamental theorem of calculus again to see that

[math]\displaystyle{ \begin{align} f(x) &= f(a)+\Big(xf'(x)-af'(a)\Big)-\int_a^x tf''(t) \, dt \\ &= f(a) + x\left(f'(a) + \int_a^x f''(t) \,dt \right) -af'(a)-\int_a^x tf''(t) \, dt \\ &= f(a)+(x-a)f'(a)+\int_a^x \, (x-t)f''(t) \, dt, \end{align} }[/math]

which is exactly Taylor's theorem with remainder in the integral form in the case [math]\displaystyle{ k=1 }[/math]. The general statement is proved using induction. Suppose that

[math]\displaystyle{ f(x) = f(a) + \frac{f'(a)}{1!}(x - a) + \cdots + \frac{f^{(k)}(a)}{k!}(x - a)^k + \int_a^x \frac{f^{(k+1)} (t)}{k!} (x - t)^k \, dt. }[/math]

(eq1)

Integrating the remainder term by parts we arrive at

[math]\displaystyle{ \begin{align} \int_a^x \frac{f^{(k+1)} (t)}{k!} (x - t)^k \, dt = & - \left[ \frac{f^{(k+1)} (t)}{(k+1)k!} (x - t)^{k+1} \right]_a^x + \int_a^x \frac{f^{(k+2)} (t)}{(k+1)k!} (x - t)^{k+1} \, dt \\ = & \ \frac{f^{(k+1)} (a)}{(k+1)!} (x - a)^{k+1} + \int_a^x \frac{f^{(k+2)} (t)}{(k+1)!} (x - t)^{k+1} \, dt. \end{align} }[/math]

Substituting this into the formula in (eq1) shows that if it holds for the value [math]\displaystyle{ k }[/math], it must also hold for the value [math]\displaystyle{ k+1 }[/math]. Therefore, since it holds for [math]\displaystyle{ k=1 }[/math], it must hold for every positive integer [math]\displaystyle{ k }[/math].

Derivation for the remainder of multivariate Taylor polynomials

We prove the special case, where [math]\displaystyle{ f:\mathbb R^n\to\mathbb R }[/math] has continuous partial derivatives up to the order [math]\displaystyle{ k+1 }[/math] in some closed ball [math]\displaystyle{ B }[/math] with center [math]\displaystyle{ \boldsymbol{a} }[/math]. The strategy of the proof is to apply the one-variable case of Taylor's theorem to the restriction of [math]\displaystyle{ f }[/math] to the line segment adjoining [math]\displaystyle{ \boldsymbol{x} }[/math] and [math]\displaystyle{ \boldsymbol{a} }[/math]. Parametrize the line segment between [math]\displaystyle{ \boldsymbol{a} }[/math] and [math]\displaystyle{ \boldsymbol{x} }[/math] by [math]\displaystyle{ \boldsymbol{u}(t)=\boldsymbol{a}+t(\boldsymbol{x}-\boldsymbol{a}) }[/math] We apply the one-variable version of Taylor's theorem to the function [math]\displaystyle{ g(t) = f(\boldsymbol{u}(t)) }[/math]:

[math]\displaystyle{ f(\boldsymbol{x})=g(1)=g(0)+\sum_{j=1}^k\frac{1}{j!}g^{(j)}(0)\ +\ \int_0^1 \frac{(1-t)^k }{k!} g^{(k+1)}(t)\, dt. }[/math]

Applying the chain rule for several variables gives

[math]\displaystyle{ \begin{align} g^{(j)}(t)&=\frac{d^j}{dt^j}f(\boldsymbol{u}(t))\\ &= \frac{d^j}{dt^j} f(\boldsymbol{a}+t(\boldsymbol{x}-\boldsymbol{a}))\\ &= \sum_{|\alpha| =j} \left(\begin{matrix} j\\ \alpha\end{matrix} \right) (D^\alpha f) (\boldsymbol{a}+t(\boldsymbol{x}-\boldsymbol{a})) (\boldsymbol{x}-\boldsymbol{a})^\alpha \end{align} }[/math]

where [math]\displaystyle{ \tbinom j \alpha }[/math] is the multinomial coefficient. Since [math]\displaystyle{ \tfrac{1}{j!}\tbinom j \alpha=\tfrac{1}{\alpha!} }[/math], we get:

[math]\displaystyle{ f(\boldsymbol{x})= f(\boldsymbol{a}) + \sum_{1 \leq |\alpha| \leq k}\frac{1}{\alpha!} (D^\alpha f) (\boldsymbol{a})(\boldsymbol{x}-\boldsymbol{a})^\alpha+\sum_{|\alpha|=k+1}\frac{k+1}{\alpha!} (\boldsymbol{x}-\boldsymbol{a})^\alpha \int_0^1 (1-t)^k (D^\alpha f)(\boldsymbol{a}+t(\boldsymbol{x}-\boldsymbol{a}))\,dt. }[/math]

See also

• Hadamard's lemma
• Laurent series – Power series with negative powers
• Padé approximant – 'Best' approximation of a function by a rational function of given order

References

• Apostol, Tom (1967), Calculus, Wiley, ISBN 0-471-00005-1, https://archive.org/details/calculus01apos .
• Apostol, Tom (1974), Mathematical analysis, Addison–Wesley .
• Bartle, Robert G.; Sherbert, Donald R. (2011), Introduction to Real Analysis (4th ed.), Wiley, ISBN 978-0-471-43331-6 .
• Hörmander, L. (1976), Linear Partial Differential Operators, Volume 1, Springer, ISBN 978-3-540-00662-6 .
• Kline, Morris (1972), Mathematical thought from ancient to modern times, Volume 2, Oxford University Press .
• Kline, Morris (1998), Calculus: An Intuitive and Physical Approach, Dover, ISBN 0-486-40453-6 .
• Pedrick, George (1994), A First Course in Analysis, Springer, ISBN 0-387-94108-8, https://archive.org/details/firstcourseinana0000pedr .
• Stromberg, Karl (1981), Introduction to classical real analysis, Wadsworth, ISBN 978-0-534-98012-2 .
• Rudin, Walter (1987), Real and complex analysis (3rd ed.), McGraw-Hill, ISBN 0-07-054234-1 .
• Tao, Terence (2014), Analysis, Volume I (3rd ed.), Hindustan Book Agency, ISBN 978-93-80250-64-9 .
• Proof of Taylor's Theorem, Chinese University of Hong Kong, https://www.math.cuhk.edu.hk/course_builder/1516/math1010c/Taylor.pdf .

External links

• Taylor's theorem at ProofWiki
• Taylor Series Approximation to Cosine at cut-the-knot
• Trigonometric Taylor Expansion interactive demonstrative applet
• Taylor Series Revisited at Holistic Numerical Methods Institute