Shell integration

Short description: Method for calculating the volume of a solid of revolution

A volume is approximated by a collection of hollow cylinders. As the cylinder walls get thinner the approximation gets better. The limit of this approximation is the shell integral.

Shell integration (the shell method in integral calculus) is a method for calculating the volume of a solid of revolution, when integrating along an axis perpendicular to the axis of revolution. This is in contrast to disc integration which integrates along the axis parallel to the axis of revolution.

Definition

The shell method goes as follows: Consider a volume in three dimensions obtained by rotating a cross-section in the xy-plane around the y-axis. Suppose the cross-section is defined by the graph of the positive function f(x) on the interval [a, b]. Then the formula for the volume will be:

$2\pi \underset{a}{\overset{b}{\int }}xf(x)dx$

If the function is of the y coordinate and the axis of rotation is the x-axis then the formula becomes:

$2\pi \underset{a}{\overset{b}{\int }}yf(y)dy$

If the function is rotating around the line x = h then the formula becomes:

$\{\begin{array}{ll}2\pi \underset{a}{\overset{b}{\int }}(x-h)f(x)dx,& \text{if}h\le a<b\\ 2\pi \underset{a}{\overset{b}{\int }}(h-x)f(x)dx,& \text{if}a<b\le h,\end{array}$

and for rotations around y = k it becomes

$\{\begin{array}{ll}2\pi \underset{a}{\overset{b}{\int }}(y-k)f(y)dy,& \text{if}k\le a<b\\ 2\pi \underset{a}{\overset{b}{\int }}(k-y)f(y)dy,& \text{if}a<b\le k.\end{array}$

The formula is derived by computing the double integral in polar coordinates.

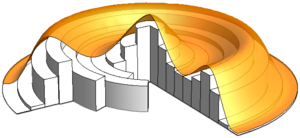
Derivation of the formula

A way to obtain the formula The method's formula can be derived as follows:

Consider the function $f(x)$ which describes our cross-section of the solid, now the integral of the function can be described as a Riemann integral: $\underset{a}{\overset{b}{\int }}f(x)dx=\underset{n\to \mathrm{\infty }}{\lim }\sum _{i=1}^{n}f(a+i\mathrm{\Delta }x)\mathrm{\Delta }x$

Where $\mathrm{\Delta }x=\frac{b-a}{n}$ is a small difference in $x$

The Riemann sum can be thought up as a sum of a number n of rectangles with ever shrinking bases, we might focus on one of them:

$f(a+k\mathrm{\Delta }x)\mathrm{\Delta }x$

Now, when we rotate the function around the axis of revolution, it is equivalent to rotating all of these rectangles around said axis, these rectangles end up becoming a hollow cylinder, composed by the difference of two normal cylinders. For our chosen rectangle, its made by obtaining a cylinder of radius $a+(k+1)\mathrm{\Delta }x$ with height $f(a+k\mathrm{\Delta }x)$ , and substracting it another smaller cylinder of radius $a+k\mathrm{\Delta }x$, with the same height of $f(a+k\mathrm{\Delta }x)$ , this difference of cylinder volumes is:

$\pi (a+(k+1)\mathrm{\Delta }x{)}^{2}f(a+k\mathrm{\Delta }x)-\pi (a+k\mathrm{\Delta }x{)}^{2}f(a+k\mathrm{\Delta }x)$

$=\pi f(a+k\mathrm{\Delta }x)((a+(k+1)\mathrm{\Delta }x{)}^2-(a+k\mathrm{\Delta }x{)}^2)$

By difference of squares , the last factor can be reduced as:

$\pi f(a+k\mathrm{\Delta }x)(2a+2k\mathrm{\Delta }x+\mathrm{\Delta }x)\mathrm{\Delta }x$

The third factor can be factored out by two, ending up as:

$2\pi f(a+k\mathrm{\Delta }x)(a+k\mathrm{\Delta }x+\frac{\mathrm{\Delta }x}{2})\mathrm{\Delta }x$

This same thing happens with all terms, so our total sum becomes:

$\underset{n\to \mathrm{\infty }}{\lim }2\pi \sum _{i=1}^{n}f(a+i\mathrm{\Delta }x)(a+i\mathrm{\Delta }x+\frac{\mathrm{\Delta }x}{2})\mathrm{\Delta }x$

In the limit of $n\to \mathrm{\infty }$, we can clearly identify that:

• $f(a+i\mathrm{\Delta }x)$ as $\mathrm{\Delta }x$ tends to 0 ends up becoming $f(x)$
• $(a+i\mathrm{\Delta }x+\frac{\mathrm{\Delta }x}{2})$ becomes $x$ itself, going from a to b (ignoring the last term which vanishes)
• $\mathrm{\Delta }x$ becomes the infinitesimal $dx$

Thus, at the limit of infinity, the sum becomes the integral:

$2\pi \underset{a}{\overset{b}{\int }}xf(x)dx$

QED $◻$.

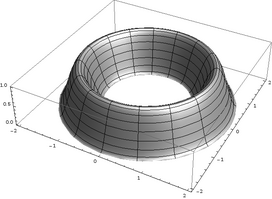
Example

Consider the volume, depicted below, whose cross section on the interval [1, 2] is defined by:

$y=8(x-1{)}^2(x-2{)}^2$

Cross-section

3D volume

With the shell method we simply use the following formula:

$V=16\pi \underset{1}{\overset{2}{\int }}x((x-1{)}^2(x-2{)}^2)dx$

By expanding the polynomial, the integration is easily done giving ⁠8/10⁠$\pi$ cubic units.

Comparison With Disc Integration

Much more work is needed to find the volume if we use disc integration. First, we would need to solve $y=8(x-1{)}^2(x-2{)}^2$ for x. Next, because the volume is hollow in the middle, we would need two functions: one that defined an outer solid and one that defined the inner hollow. After integrating each of these two functions, we would subtract them to yield the desired volume.

See also

• Solid of revolution
• Disc integration

References

• Weisstein, Eric W.. "Method of Shells". http://mathworld.wolfram.com/MethodofShells.html. 
• Frank Ayres, Elliott Mendelson. Schaum's Outlines: Calculus. McGraw-Hill Professional 2008, ISBN 978-0-07-150861-2. pp. 244–248 (online copy, p. 244, at Google Books)