Second Hardy–Littlewood conjecture
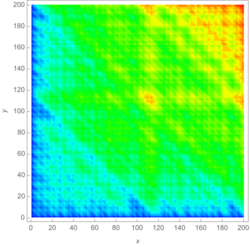 Plot of [math]\displaystyle{ \pi(x) + \pi(y) - \pi(x+y) }[/math] for [math]\displaystyle{ x, y \leq 200 }[/math] | |
| Field | Number theory |
|---|---|
| Conjectured by | G. H. Hardy John Edensor Littlewood |
| Conjectured in | 1923 |
| Open problem | yes |
In number theory, the second Hardy–Littlewood conjecture concerns the number of primes in intervals. Along with the first Hardy–Littlewood conjecture, the second Hardy–Littlewood conjecture was proposed by G. H. Hardy and John Edensor Littlewood in 1923.[1]
Statement
The conjecture states that
[math]\displaystyle{ \pi(x+y) \leq \pi(x) + \pi(y) }[/math]
for integers x, y ≥ 2, where π(z) denotes the prime-counting function, giving the number of prime numbers up to and including z.
Connection to the first Hardy–Littlewood conjecture
The statement of the second Hardy–Littlewood conjecture is equivalent to the statement that the number of primes from x + 1 to x + y is always less than or equal to the number of primes from 1 to y. This was proved to be inconsistent with the first Hardy–Littlewood conjecture on prime k-tuples, and the first violation is expected to likely occur for very large values of x.[2][3] For example, an admissible k-tuple (or prime constellation) of 447 primes can be found in an interval of y = 3159 integers, while π(3159) = 446. If the first Hardy–Littlewood conjecture holds, then the first such k-tuple is expected for x greater than 1.5 × 10174 but less than 2.2 × 101198.[4]
References
- ↑ Hardy, G. H.; Littlewood, J. E. (1923). "Some Problems of 'Partitio Numerorum.' III. On the Expression of a Number as a Sum of Primes.". Acta Math. 44 (44): 1–70. doi:10.1007/BF02403921..
- ↑ Hensley, Douglas; Richards, Ian. "Primes in intervals". Acta Arith. 25 (1973/74): 375–391. doi:10.4064/aa-25-4-375-391.
- ↑ Richards, Ian (1974). "On the Incompatibility of Two Conjectures Concerning Primes". Bull. Amer. Math. Soc. 80: 419–438. doi:10.1090/S0002-9904-1974-13434-8.
- ↑ "447-tuple calculations". http://www.opertech.com/primes/residues.html. Retrieved 2008-08-12.
External links
- Engelsma, Thomas J.. "k-tuple Permissible Patterns". http://www.opertech.com/primes/k-tuples.html. Retrieved 2008-08-12.
- Oliveira e Silva, Tomás. "Admissible prime constellations". https://sweet.ua.pt/tos/apc.html. Retrieved 2023-09-28.
 |

