Half-transitive graph

Graph families defined by their automorphisms
distance-transitive	→	distance-regular	←	strongly regular
↓
symmetric (arc-transitive)	←	t-transitive, t ≥ 2		skew-symmetric
↓
(if connected) vertex- and edge-transitive	→	edge-transitive and regular	→	edge-transitive
↓		↓		↓
vertex-transitive	→	regular	→	(if bipartite) biregular
↑
Cayley graph	←	zero-symmetric		asymmetric

In the mathematical field of graph theory, a half-transitive graph is a graph that is both vertex-transitive and edge-transitive, but not symmetric. In other words, a graph is half-transitive if its automorphism group acts transitively upon both its vertices and its edges, but not on ordered pairs of linked vertices.

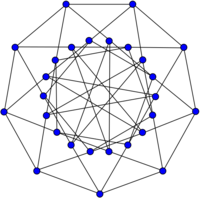
The Holt graph is the smallest half-transitive graph. The lack of reflectional symmetry in this drawing highlights the fact that edges are not equivalent to their inverse.

Every connected symmetric graph must be vertex-transitive and edge-transitive, and the converse is true for graphs of odd degree, so that half-transitive graphs of odd degree do not exist. However, there do exist half-transitive graphs of even degree. The smallest half-transitive graph is the Holt graph, with degree 4 and 27 vertices.