Astronomy:Curved space

Curved space often refers to a spatial geometry which is not "flat", where a flat space has zero curvature, as described by Euclidean geometry. Curved spaces can generally be described by Riemannian geometry, though some simple cases can be described in other ways. Curved spaces play an essential role in general relativity, where gravity is often visualized as curved space. The Friedmann–Lemaître–Robertson–Walker metric is a curved metric which forms the current foundation for the description of the expansion of space and shape of the universe.

Simple two-dimensional example

A very familiar example of a curved space is the surface of a sphere. While to our familiar outlook the sphere looks three-dimensional, if an object is constrained to lie on the surface, it only has two dimensions that it can move in. The surface of a sphere can be completely described by two dimensions, since no matter how rough the surface may appear to be, it is still only a surface, which is the two-dimensional outside border of a volume. Even the surface of the Earth, which is fractal in complexity, is still only a two-dimensional boundary along the outside of a volume.

Embedding

In a flat space, the sum of the squares of the side of a right-angled triangle is equal to the square of the hypotenuse. This relationship does not hold for curved spaces.

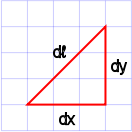
One of the defining characteristics of a curved space is its departure from the Pythagorean theorem. In a curved space

[math]\displaystyle{ dx^2 + dy^2 \neq dl^2 }[/math].

The Pythagorean relationship can often be restored by describing the space with an extra dimension. Suppose we have a three-dimensional non-Euclidean space with coordinates [math]\displaystyle{ \left(x',y',z'\right) }[/math]. Because it is not flat

[math]\displaystyle{ dx'^2 + dy'^2 + dz'^2 \ne dl'^2 \, }[/math].

But if we now describe the three-dimensional space with four dimensions ([math]\displaystyle{ x,y,z,w }[/math]) we can choose coordinates such that

[math]\displaystyle{ dx^2 + dy^2 + dz^2 + dw^2 = dl^2 \, }[/math].

Note that the coordinate [math]\displaystyle{ x }[/math] is not the same as the coordinate [math]\displaystyle{ x' }[/math].

For the choice of the 4D coordinates to be valid descriptors of the original 3D space it must have the same number of degrees of freedom. Since four coordinates have four degrees of freedom it must have a constraint placed on it. We can choose a constraint such that Pythagorean theorem holds in the new 4D space. That is

[math]\displaystyle{ x^2 + y^2 + z^2 +w^2 = \textrm{constant} \, }[/math].

The constant can be positive or negative. For convenience we can choose the constant to be

[math]\displaystyle{ \kappa^{-1}R^2 }[/math] where [math]\displaystyle{ R^2 \, }[/math] now is positive and [math]\displaystyle{ \kappa \equiv \plusmn 1 }[/math].

We can now use this constraint to eliminate the artificial fourth coordinate [math]\displaystyle{ w }[/math]. The differential of the constraining equation is

[math]\displaystyle{ xdx + ydy + zdz + wdw = 0 \, }[/math] leading to [math]\displaystyle{ dw = -w^{-1}(xdx + ydy +zdz) \, }[/math].

Plugging [math]\displaystyle{ dw }[/math] into the original equation gives

[math]\displaystyle{ dl^2 = dx^2 + dy^2 + dz^2 + \frac{(xdx+ydy+zdz)^2}{\kappa^{-1}R^2 - x^2 - y^2 - z^2} }[/math].

This form is usually not particularly appealing and so a coordinate transform is often applied: [math]\displaystyle{ x = r\sin\theta\cos\phi }[/math], [math]\displaystyle{ y = r\sin\theta\sin\phi }[/math], [math]\displaystyle{ z = r\cos\theta }[/math]. With this coordinate transformation

[math]\displaystyle{ dl^2 = \frac{dr^2}{1-\kappa\frac{r^2}{R^2}} + r^2d\theta^2 + r^2\sin^2\theta d\phi^2 }[/math].

Without embedding

The geometry of a n-dimensional space can also be described with Riemannian geometry. An isotropic and homogeneous space can be described by the metric:

[math]\displaystyle{ dl^2 = e^{-\lambda(r)}{dr^2} + r^2d\theta^2 + r^2\sin^2\theta d\phi^2 \, }[/math].

This reduces to Euclidean space when [math]\displaystyle{ \lambda = 0 }[/math]. But a space can be said to be "flat" when the Weyl tensor has all zero components. In three dimensions this condition is met when the Ricci tensor ([math]\displaystyle{ R_{ab} }[/math]) is equal to the metric times the Ricci scalar ([math]\displaystyle{ R }[/math], not to be confused with the R of the previous section). That is [math]\displaystyle{ R_{ab} = g_{ab} R }[/math]. Calculation of these components from the metric gives that

[math]\displaystyle{ \lambda = -\frac{1}{2}\ln \left( 1 - k r^2 \right) }[/math] where [math]\displaystyle{ k \equiv \frac{R}{2} }[/math].

This gives the metric:

[math]\displaystyle{ dl^2 = \frac{dr^2}{1-k{r^2}} + r^2d\theta^2 + r^2\sin^2\theta d\phi^2 }[/math].

where [math]\displaystyle{ k }[/math] can be zero, positive, or negative and is not limited to ±1.

Open, flat, closed

An isotropic and homogeneous space can be described by the metric:

[math]\displaystyle{ dl^2 = \frac{dr^2}{1-\kappa\frac{r^2}{R^2}} + r^2d\theta^2 + r^2\sin^2\theta d\phi^2 }[/math].

In the limit that the constant of curvature ([math]\displaystyle{ R }[/math]) becomes infinitely large, a flat, Euclidean space is returned. It is essentially the same as setting [math]\displaystyle{ \kappa }[/math] to zero. If [math]\displaystyle{ \kappa }[/math] is not zero the space is not Euclidean. When [math]\displaystyle{ \kappa = +1 }[/math] the space is said to be closed or elliptic. When [math]\displaystyle{ \kappa = -1 }[/math] the space is said to be open or hyperbolic.

Triangles which lie on the surface of an open space will have a sum of angles which is less than 180°. Triangles which lie on the surface of a closed space will have a sum of angles which is greater than 180°. The volume, however, is not [math]\displaystyle{ (4/3)\pi r^3 }[/math].

See also

• CAT(k) space
• Non-positive curvature

Further reading

• The Feynman Lectures on Physics Vol. II Ch. 42: Curved Space
• Papastavridis, John G. (1999). "General n-Dimensional (Riemannian) Surfaces". Tensor Calculus and Analytical Dynamics. Boca Raton: CRC Press. pp. 211–218. ISBN 0-8493-8514-8. https://books.google.com/books?id=pgCx01lds9UC&pg=PA211. 

External links

• Curved Spaces, simulator for multi-connected universes developed by Jeffrey Weeks