Beta prime distribution

Short description: Probability distribution

Beta prime

Probability density function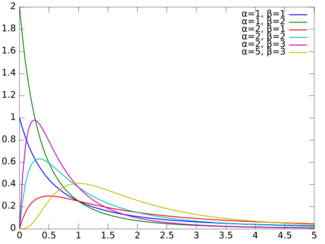
Cumulative distribution function
Parameters	[math]\displaystyle{ \alpha \gt 0 }[/math] shape (real) [math]\displaystyle{ \beta \gt 0 }[/math] shape (real)
Support	[math]\displaystyle{ x \in [0,\infty)\! }[/math]
PDF	[math]\displaystyle{ f(x) = \frac{x^{\alpha-1} (1+x)^{-\alpha -\beta}}{B(\alpha,\beta)}\! }[/math]
CDF	[math]\displaystyle{ I_{\frac{x}{1+x}(\alpha,\beta) } }[/math] where [math]\displaystyle{ I_x(\alpha,\beta) }[/math] is the incomplete beta function
Mean	[math]\displaystyle{ \frac{\alpha}{\beta-1} \text{ if } \beta\gt 1 }[/math]
Mode	[math]\displaystyle{ \frac{\alpha-1}{\beta+1} \text{ if } \alpha\ge 1\text{, 0 otherwise}\! }[/math]
Variance	[math]\displaystyle{ \frac{\alpha(\alpha+\beta-1)}{(\beta-2)(\beta-1)^2} \text{ if } \beta\gt 2 }[/math]
Skewness	[math]\displaystyle{ \frac{2(2\alpha+\beta-1)}{\beta-3}\sqrt{\frac{\beta-2}{\alpha(\alpha+\beta-1)}} \text{ if } \beta\gt 3 }[/math]
MGF	Does not exist
CF	[math]\displaystyle{ \frac{e^{-it}\Gamma(\alpha+\beta)}{\Gamma(\beta)}G_{1,2}^{\,2,0}\!\left(\left.{\begin{matrix}\alpha+\beta\\\beta,0\end{matrix}}\;\right|\,-it\right) }[/math]

In probability theory and statistics, the beta prime distribution (also known as inverted beta distribution or beta distribution of the second kind) is an absolutely continuous probability distribution. If [math]\displaystyle{ p\in[0,1] }[/math] has a beta distribution, then the odds [math]\displaystyle{ \frac{p}{1-p} }[/math] has a beta prime distribution.

Definitions

Beta prime distribution is defined for [math]\displaystyle{ x \gt 0 }[/math] with two parameters α and β, having the probability density function:

[math]\displaystyle{ f(x) = \frac{x^{\alpha-1} (1+x)^{-\alpha -\beta}}{B(\alpha,\beta)} }[/math]

where B is the Beta function.

The cumulative distribution function is

[math]\displaystyle{ F(x; \alpha,\beta)=I_{\frac{x}{1+x}}\left(\alpha, \beta \right) , }[/math]

where I is the regularized incomplete beta function.

The expected value, variance, and other details of the distribution are given in the sidebox; for [math]\displaystyle{ \beta\gt 4 }[/math], the excess kurtosis is

[math]\displaystyle{ \gamma_2 = 6\frac{\alpha(\alpha+\beta-1)(5\beta-11) + (\beta-1)^2(\beta-2)}{\alpha(\alpha+\beta-1)(\beta-3)(\beta-4) }. }[/math]

While the related beta distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed as a probability, the beta prime distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed in odds. The distribution is a Pearson type VI distribution.

The mode of a variate X distributed as [math]\displaystyle{ \beta'(\alpha,\beta) }[/math] is [math]\displaystyle{ \hat{X} = \frac{\alpha-1}{\beta+1} }[/math]. Its mean is [math]\displaystyle{ \frac{\alpha}{\beta-1} }[/math] if [math]\displaystyle{ \beta\gt 1 }[/math] (if [math]\displaystyle{ \beta \leq 1 }[/math] the mean is infinite, in other words it has no well defined mean) and its variance is [math]\displaystyle{ \frac{\alpha(\alpha+\beta-1)}{(\beta-2)(\beta-1)^2} }[/math] if [math]\displaystyle{ \beta\gt 2 }[/math].

For [math]\displaystyle{ -\alpha \lt k \lt \beta }[/math], the k-th moment [math]\displaystyle{ E[X^k] }[/math] is given by

[math]\displaystyle{ E[X^k]=\frac{B(\alpha+k,\beta-k)}{B(\alpha,\beta)}. }[/math]

For [math]\displaystyle{ k\in \mathbb{N} }[/math] with [math]\displaystyle{ k \lt \beta, }[/math] this simplifies to

[math]\displaystyle{ E[X^k]=\prod_{i=1}^k \frac{\alpha+i-1}{\beta-i}. }[/math]

The cdf can also be written as

[math]\displaystyle{ \frac{x^\alpha \cdot {}_2F_1(\alpha, \alpha+\beta, \alpha+1, -x)}{\alpha \cdot B(\alpha,\beta)} }[/math]

where [math]\displaystyle{ {}_2F_1 }[/math] is the Gauss's hypergeometric function ₂F₁ .

Alternative parameterization

The beta prime distribution may also be reparameterized in terms of its mean μ > 0 and precision ν > 0 parameters ( p. 36).

Consider the parameterization μ = α/(β-1) and ν = β- 2, i.e., α = μ( 1 + ν) and β = 2 + ν. Under this parameterization E[Y] = μ and Var[Y] = μ(1 + μ)/ν.

Generalization

Two more parameters can be added to form the generalized beta prime distribution [math]\displaystyle{ \beta'(\alpha,\beta,p,q) }[/math]:

• [math]\displaystyle{ p \gt 0 }[/math] shape (real)
• [math]\displaystyle{ q \gt 0 }[/math] scale (real)

having the probability density function:

[math]\displaystyle{ f(x;\alpha,\beta,p,q) = \frac{p \left(\frac x q \right)^{\alpha p-1} \left(1+ \left(\frac x q \right)^p\right)^{-\alpha -\beta}}{qB(\alpha,\beta)} }[/math]

with mean

[math]\displaystyle{ \frac{q\Gamma\left(\alpha+\tfrac 1 p\right)\Gamma(\beta-\tfrac 1 p)}{\Gamma(\alpha)\Gamma(\beta)} \quad \text{if } \beta p\gt 1 }[/math]

and mode

[math]\displaystyle{ q \left({\frac{\alpha p -1}{\beta p +1}}\right)^\tfrac{1}{p} \quad \text{if } \alpha p\ge 1 }[/math]

Note that if p = q = 1 then the generalized beta prime distribution reduces to the standard beta prime distribution.

This generalization can be obtained via the following invertible transformation. If [math]\displaystyle{ y\sim\beta'(\alpha,\beta) }[/math] and [math]\displaystyle{ x=qy^{1/p} }[/math] for [math]\displaystyle{ q,p\gt 0 }[/math], then [math]\displaystyle{ x\sim\beta'(\alpha,\beta,p,q) }[/math].

Compound gamma distribution

The compound gamma distribution is the generalization of the beta prime when the scale parameter, q is added, but where p = 1. It is so named because it is formed by compounding two gamma distributions:

[math]\displaystyle{ \beta'(x;\alpha,\beta,1,q) = \int_0^\infty G(x;\alpha,r)G(r;\beta,q) \; dr }[/math]

where [math]\displaystyle{ G(x;a,b) }[/math] is the gamma pdf with shape [math]\displaystyle{ a }[/math] and inverse scale [math]\displaystyle{ b }[/math].

The mode, mean and variance of the compound gamma can be obtained by multiplying the mode and mean in the above infobox by q and the variance by q².

Another way to express the compounding is if [math]\displaystyle{ r\sim G(\beta,q) }[/math] and [math]\displaystyle{ x\mid r\sim G(\alpha,r) }[/math], then [math]\displaystyle{ x\sim\beta'(\alpha,\beta,1,q) }[/math]. (This gives one way to generate random variates with compound gamma, or beta prime distributions. Another is via the ratio of independent gamma variates, as shown below.)

Properties

• If [math]\displaystyle{ X \sim \beta'(\alpha,\beta) }[/math] then [math]\displaystyle{ \tfrac{1}{X} \sim \beta'(\beta,\alpha) }[/math].
• If [math]\displaystyle{ Y\sim\beta'(\alpha,\beta) }[/math], and [math]\displaystyle{ X=qY^{1/p} }[/math], then [math]\displaystyle{ X\sim\beta'(\alpha,\beta,p,q) }[/math].
• If [math]\displaystyle{ X \sim \beta'(\alpha,\beta,p,q) }[/math] then [math]\displaystyle{ kX \sim \beta'(\alpha,\beta,p,kq) }[/math].
• [math]\displaystyle{ \beta'(\alpha,\beta,1,1) = \beta'(\alpha,\beta) }[/math]
• If [math]\displaystyle{ X_1 \sim \beta'(\alpha,\beta) }[/math] and [math]\displaystyle{ X_2 \sim \beta'(\alpha,\beta) }[/math] two iid variables, then [math]\displaystyle{ Y=X_1+X_2 \sim \beta'(\gamma,\delta) }[/math] with [math]\displaystyle{ \gamma=\frac{2\alpha(\alpha +\beta^2 - 2\beta + 2\alpha\beta -4\alpha+1)}{(\beta-1)(\alpha+\beta-1)} }[/math] and [math]\displaystyle{ \delta =\frac{2\alpha +\beta^2-\beta +2\alpha \beta-4\alpha}{\alpha +\beta -1} }[/math], as the beta prime distribution is infinitely divisible.
• More generally, let [math]\displaystyle{ X_1,...,X_n n }[/math] iid variables following the same beta prime distribution, i.e. [math]\displaystyle{ \forall i, 1\leq i\leq n, X_i \sim \beta'(\alpha,\beta) }[/math], then the sum [math]\displaystyle{ S=X_1+...+X_n \sim \beta'(\gamma,\delta) }[/math] with [math]\displaystyle{ \gamma=\frac{n\alpha(\alpha +\beta^2 - 2\beta + n\alpha\beta -2n\alpha+1)}{(\beta-1)(\alpha+\beta-1)} }[/math] and [math]\displaystyle{ \delta =\frac{2\alpha +\beta^2-\beta +n\alpha \beta-2n\alpha}{\alpha +\beta -1} }[/math].

Related distributions

• If [math]\displaystyle{ X \sim F(2\alpha,2\beta) }[/math] has an F-distribution, then [math]\displaystyle{ \tfrac{\alpha}{\beta} X \sim \beta'(\alpha,\beta) }[/math], or equivalently, [math]\displaystyle{ X\sim\beta'(\alpha,\beta , 1 , \tfrac{\beta}{\alpha}) }[/math].
• If [math]\displaystyle{ X \sim \textrm{Beta}(\alpha,\beta) }[/math] then [math]\displaystyle{ \frac{X}{1-X} \sim \beta'(\alpha,\beta) }[/math].
• If [math]\displaystyle{ X \sim \beta'(\alpha,\beta) }[/math] then [math]\displaystyle{ \frac{X}{1+X} \sim \textrm{Beta}(\alpha,\beta) }[/math].
• For gamma distribution parametrization I:
  • If [math]\displaystyle{ X_k \sim \Gamma(\alpha_k,\theta_k) }[/math] are independent, then [math]\displaystyle{ \tfrac{X_1}{X_2} \sim \beta'(\alpha_1,\alpha_2,1,\tfrac{\theta_1}{\theta_2}) }[/math]. Note [math]\displaystyle{ \theta_1,\theta_2,\tfrac{\theta_1}{\theta_2} }[/math] are all scale parameters for their respective distributions.
• For gamma distribution parametrization II:
  • If [math]\displaystyle{ X_k \sim \Gamma(\alpha_k,\beta_k) }[/math] are independent, then [math]\displaystyle{ \tfrac{X_1}{X_2} \sim \beta'(\alpha_1,\alpha_2,1,\tfrac{\beta_2}{\beta_1}) }[/math]. The [math]\displaystyle{ \beta_k }[/math] are rate parameters, while [math]\displaystyle{ \tfrac{\beta_2}{\beta_1} }[/math] is a scale parameter.
  • If [math]\displaystyle{ \beta_2\sim \Gamma(\alpha_1,\beta_1) }[/math] and [math]\displaystyle{ X_2\mid\beta_2\sim\Gamma(\alpha_2,\beta_2) }[/math], then [math]\displaystyle{ X_2\sim\beta'(\alpha_2,\alpha_1,1,\beta_1) }[/math]. The [math]\displaystyle{ \beta_k }[/math] are rate parameters for the gamma distributions, but [math]\displaystyle{ \beta_1 }[/math] is the scale parameter for the beta prime.
• [math]\displaystyle{ \beta'(p,1,a,b) = \textrm{Dagum}(p,a,b) }[/math] the Dagum distribution
• [math]\displaystyle{ \beta'(1,p,a,b) = \textrm{SinghMaddala}(p,a,b) }[/math] the Singh–Maddala distribution.
• [math]\displaystyle{ \beta'(1,1,\gamma,\sigma) = \textrm{LL}(\gamma,\sigma) }[/math] the log logistic distribution.
• The beta prime distribution is a special case of the type 6 Pearson distribution.
• If X has a Pareto distribution with minimum [math]\displaystyle{ x_m }[/math] and shape parameter [math]\displaystyle{ \alpha }[/math], then [math]\displaystyle{ \dfrac{X}{x_m}-1\sim\beta^\prime(1,\alpha) }[/math].
• If X has a Lomax distribution, also known as a Pareto Type II distribution, with shape parameter [math]\displaystyle{ \alpha }[/math] and scale parameter [math]\displaystyle{ \lambda }[/math], then [math]\displaystyle{ \frac{X}{\lambda}\sim \beta^\prime(1,\alpha) }[/math].
• If X has a standard Pareto Type IV distribution with shape parameter [math]\displaystyle{ \alpha }[/math] and inequality parameter [math]\displaystyle{ \gamma }[/math], then [math]\displaystyle{ X^{\frac{1}{\gamma}} \sim \beta^\prime(1,\alpha) }[/math], or equivalently, [math]\displaystyle{ X \sim \beta^\prime(1,\alpha,\tfrac{1}{\gamma},1) }[/math].
• The inverted Dirichlet distribution is a generalization of the beta prime distribution.
• If [math]\displaystyle{ X\sim\beta'(\alpha,\beta) }[/math], then [math]\displaystyle{ \ln X }[/math] has a generalized logistic distribution. More generally, if [math]\displaystyle{ X\sim\beta'(\alpha,\beta,p,q) }[/math], then [math]\displaystyle{ \ln X }[/math] has a scaled and shifted generalized logistic distribution.

References

• Johnson, N.L., Kotz, S., Balakrishnan, N. (1995). Continuous Univariate Distributions, Volume 2 (2nd Edition), Wiley. ISBN:0-471-58494-0
• Bourguignon, M.; Santos-Neto, M.; de Castro, M. (2021), "A new regression model for positive random variables with skewed and long tail", Metron 79: 33–55, doi:10.1007/s40300-021-00203-y 

• MathWorld article