Binomial proportion confidence interval
In statistics, a binomial proportion confidence interval is a confidence interval for the probability of success calculated from the outcome of a series of success–failure experiments (Bernoulli trials). In other words, a binomial proportion confidence interval is an interval estimate of a success probability p when only the number of experiments n and the number of successes nS are known.
There are several formulas for a binomial confidence interval, but all of them rely on the assumption of a binomial distribution. In general, a binomial distribution applies when an experiment is repeated a fixed number of times, each trial of the experiment has two possible outcomes (success and failure), the probability of success is the same for each trial, and the trials are statistically independent. Because the binomial distribution is a discrete probability distribution (i.e., not continuous) and difficult to calculate for large numbers of trials, a variety of approximations are used to calculate this confidence interval, all with their own tradeoffs in accuracy and computational intensity.
A simple example of a binomial distribution is the set of various possible outcomes, and their probabilities, for the number of heads observed when a coin is flipped ten times. The observed binomial proportion is the fraction of the flips that turn out to be heads. Given this observed proportion, the confidence interval for the true probability of the coin landing on heads is a range of possible proportions, which may or may not contain the true proportion. A 95% confidence interval for the proportion, for instance, will contain the true proportion 95% of the times that the procedure for constructing the confidence interval is employed.[1]
Normal approximation interval or Wald interval
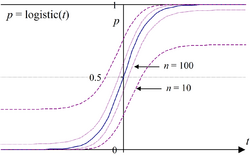
A commonly used formula for a binomial confidence interval relies on approximating the distribution of error about a binomially-distributed observation, [math]\displaystyle{ \hat p }[/math], with a normal distribution.[3] This approximation is based on the central limit theorem and is unreliable when the sample size is small or the success probability is close to 0 or 1.[4]
Using the normal approximation, the success probability p is estimated as
- [math]\displaystyle{ \hat p \pm z \sqrt{\frac{\hat p \left(1 - \hat p\right)}{n}}, }[/math]
or the equivalent
- [math]\displaystyle{ \frac{n_S}{n} \pm \frac{z}{n \sqrt{n}} \sqrt{n_S n_F}, }[/math]
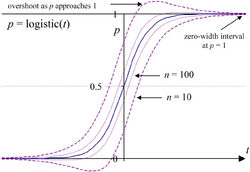
where [math]\displaystyle{ \hat p = n_S / n }[/math] is the proportion of successes in a Bernoulli trial process, measured with [math]\displaystyle{ n }[/math] trials yielding [math]\displaystyle{ n_S }[/math] successes and [math]\displaystyle{ n_F = n - n_S }[/math] failures, and [math]\displaystyle{ z }[/math] is the [math]\displaystyle{ 1 - \tfrac{\alpha}{2} }[/math] quantile of a standard normal distribution (i.e., the probit) corresponding to the target error rate [math]\displaystyle{ \alpha }[/math]. For a 95% confidence level, the error [math]\displaystyle{ \alpha=1-0.95=0.05 }[/math], so [math]\displaystyle{ 1 - \tfrac \alpha 2=0.975 }[/math] and [math]\displaystyle{ z=1.96 }[/math]. From this one finds two problems. First, for [math]\displaystyle{ \hat p }[/math] approaching unit (or zero), the interval narrows to zero width (implying certainty). Second, for values of [math]\displaystyle{ \hat p \lt \tfrac{z^2}{z^2+n} }[/math] (or equivalently for [math]\displaystyle{ 1-\hat p }[/math]), the interval boundaries exceed [math]\displaystyle{ [0,1] }[/math] (overshoot).
An important theoretical derivation of this confidence interval involves the inversion of a hypothesis test. Under this formulation, the confidence interval represents those values of the population parameter that would have large p-values if they were tested as a hypothesized population proportion.[clarification needed] The collection of values, [math]\displaystyle{ \theta }[/math], for which the normal approximation is valid can be represented as
- [math]\displaystyle{ \left\{ \theta \,\,\bigg|\,\, y \le \frac{\hat p - \theta}{\sqrt{\frac{1}{n} \hat p \left(1 - \hat p\right)}} \le z_{\alpha/2} \right\}, }[/math]
where [math]\displaystyle{ y }[/math] is the [math]\displaystyle{ \tfrac \alpha 2 }[/math] quantile of a standard normal distribution.
Since the test in the middle of the inequality is a Wald test, the normal approximation interval is sometimes called the Wald interval or Wald method, after Abraham Wald, but it was first described by Pierre-Simon Laplace in 1812.[5]
Bracketing the confidence interval
Extending the normal approximation and Wald-Laplace interval concepts, Michael Short has shown that inequalities on the approximation error between the binomial distribution and the normal distribution can be used to accurately bracket the estimate of the confidence interval around [math]\displaystyle{ \hat p }[/math]:[6]
- [math]\displaystyle{ \frac{k+C_{L1}} {n+z^2} - z \sqrt{\frac{nk - k^2 + C_{L2} n -C_{L3} k + C_{L4}}{n(n+z^2)^2}} \le \hat p \le \frac{k+C_{U1}} {n+z^2} + z \sqrt{\frac{nk - k^2 + C_{U2} n -C_{U3} k + C_{U4}}{n(n+z^2)^2}} }[/math]
where [math]\displaystyle{ \hat p }[/math] is again the (unknown) proportion of successes in a Bernoulli trial process, measured with [math]\displaystyle{ n }[/math] trials yielding [math]\displaystyle{ k }[/math] successes, [math]\displaystyle{ z }[/math] is the [math]\displaystyle{ 1 - \tfrac{\alpha}{2} }[/math] quantile of a standard normal distribution (i.e., the probit) corresponding to the target error rate [math]\displaystyle{ \alpha }[/math], and the constants [math]\displaystyle{ C_{L1},C_{L2},C_{L3},C_{L4},C_{U1},C_{U2},C_{U3} }[/math] and [math]\displaystyle{ C_{U4} }[/math] are simple algebraic functions of [math]\displaystyle{ z }[/math].[6] For a fixed [math]\displaystyle{ \alpha }[/math] (and hence [math]\displaystyle{ z }[/math]), the above inequalities give easily computed one- or two-sided intervals which bracket the exact binomial upper and lower confidence limits corresponding to the error rate [math]\displaystyle{ \alpha }[/math].
Standard error of a proportion estimation when using weighted data
Let there be a simple random sample [math]\displaystyle{ X_1, \ldots, X_n }[/math] where each [math]\displaystyle{ X_i }[/math] is i.i.d from a Bernoulli(p) distribution and weight [math]\displaystyle{ w_i }[/math] is the weight for each observation. Standardize the (positive) weights [math]\displaystyle{ w_i }[/math] so they sum to 1. The weighted sample proportion is: [math]\displaystyle{ \hat p = \sum_{i=1}^n w_i X_i }[/math]. Since the [math]\displaystyle{ X_i }[/math] are independent and each one has variance [math]\displaystyle{ \text{Var}(X_i) = p(1-p) }[/math], the sampling variance of the proportion therefore is:[7]
- [math]\displaystyle{ \text{Var}(\hat p) = \sum_{i=1}^n \text{Var}(w_i X_i) = p(1-p)\sum_{i=1}^n w_i^2 }[/math].
The standard error of [math]\displaystyle{ \hat p }[/math] is the square root of this quantity. Because we do not know [math]\displaystyle{ p(1-p) }[/math], we have to estimate it. Although there are many possible estimators, a conventional one is to use [math]\displaystyle{ \hat p }[/math], the sample mean, and plug this into the formula. That gives:
- [math]\displaystyle{ \text{SE}(\hat p) = \sqrt{\hat p(1-\hat p) \sum_{i=1}^n w_i^2} }[/math]
For unweighted data, [math]\displaystyle{ w_i = 1/n }[/math], giving [math]\displaystyle{ \sum_{i=1}^n w_i^2 = 1/n }[/math]. The SE becomes [math]\displaystyle{ \sqrt{\hat p(1-\hat p)/n} }[/math], leading to the familiar formulas, showing that the calculation for weighted data is a direct generalization of them.
Wilson score interval
The Wilson score interval is an improvement over the normal approximation interval in multiple respects. It was developed by Edwin Bidwell Wilson (1927).[8] Unlike the symmetric normal approximation interval (above), the Wilson score interval is asymmetric. It does not suffer from problems of overshoot and zero-width intervals that afflict the normal interval, and it may be safely employed with small samples and skewed observations.[3] The observed coverage probability is consistently closer to the nominal value, [math]\displaystyle{ 1 - \alpha }[/math].[2]
Like the normal interval, the interval can be computed directly from a formula.
Wilson started with the normal approximation to the binomial:
- [math]\displaystyle{ z \approx \frac{~\left(\,p - \hat{p}\,\right)~}{\sigma_n} }[/math]
with the analytic formula for the sample standard deviation given by [math]\displaystyle{ \sigma_n = \sqrt{\,\frac{\,p\left(1-p\right)\,}{n}~}~. }[/math] Combining the two, and squaring out the radical, gives an equation that is quadratic in p:
- [math]\displaystyle{ \left(\, \hat{p} - p \,\right)^{2} = z^{2}\cdot\frac{\,p\left(1-p\right)\,}{n} }[/math]
Transforming the relation into a standard-form quadratic equation for p, treating [math]\displaystyle{ \hat p }[/math] and n as known values from the sample (see prior section), and using the value of z that corresponds to the desired confidence for the estimate of p gives this: [math]\displaystyle{ \left( 1 + \frac{\,z^2\,}{n} \right) p^2 + \left( - 2 {\hat p} - \frac{\,z^2\,}{n} \right) p + \biggl( {\hat p}^2 \biggr) = 0 ~, }[/math] where all of the values in parentheses are known quantities. The solution for p estimates the upper and lower limits of the confidence interval for p. Hence the probability of success p is estimated by
- [math]\displaystyle{ p \approx ( w^- , w^+ ) = \frac{1}{~1+\frac{\,z^2\,}{n}~}\left( \hat p+\frac{\,z^2\,}{2n} \right) ~ \pm ~ \frac{z}{~1+\frac{z^2}{n}~}\sqrt{\frac{\,\hat p(1-\hat p)\,}{n}+\frac{\,z^2\,}{4n^2}~} ~ }[/math]
or the equivalent
- [math]\displaystyle{ p \approx \frac{~ n_S + \tfrac{1}{2} z^2 ~}{ n + z^2 } ~ \pm ~ \frac{z}{n + z^2} \sqrt{ \frac{~n_S \, n_F~}{n} + \frac{z^2}{4} ~ }~. }[/math]
The practical observation from using this interval is that it has good properties even for a small number of trials and / or an extreme probability.
Intuitively, the center value of this interval is the weighted average of [math]\displaystyle{ \hat{p} }[/math] and [math]\displaystyle{ \tfrac{1}{2} }[/math], with [math]\displaystyle{ \hat{p} }[/math] receiving greater weight as the sample size increases. Formally, the center value corresponds to using a pseudocount of 1/2 z2, the number of standard deviations of the confidence interval: add this number to both the count of successes and of failures to yield the estimate of the ratio. For the common two standard deviations in each direction interval (approximately 95% coverage, which itself is approximately 1.96 standard deviations), this yields the estimate [math]\displaystyle{ (n_S+2)/(n+4) }[/math], which is known as the "plus four rule".
Although the quadratic can be solved explicitly, in most cases Wilson's equations can also be solved numerically using the fixed-point iteration
- [math]\displaystyle{ p_{k+1}=\hat{p} \pm z\cdot\sqrt{\frac{ p_k \cdot \left( 1 - p_k \right)}{n}} }[/math]
with [math]\displaystyle{ p_0 = \hat{p} }[/math].
The Wilson interval can also be derived from the single sample z-test or Pearson's chi-squared test with two categories. The resulting interval,
- [math]\displaystyle{ \left\{ \theta \,\,\bigg|\,\, y \le \frac{\hat{p} - \theta}{\sqrt{\tfrac{1}{n} \theta(1 - \theta)}} \le z \right\}, }[/math]
can then be solved for [math]\displaystyle{ \theta }[/math] to produce the Wilson score interval. The test in the middle of the inequality is a score test.
The interval equality principle
Since the interval is derived by solving from the normal approximation to the binomial, the Wilson score interval [math]\displaystyle{ ( w^- , w^+ ) }[/math] has the property of being guaranteed to obtain the same result as the equivalent z-test or chi-squared test.
This property can be visualised by plotting the probability density function for the Wilson score interval (see Wallis 2021: 297-313)[9] and then plotting a normal pdf at each bound. The tail areas of the resulting Wilson and normal distributions, representing the chance of a significant result in that direction, must be equal.
The continuity-corrected Wilson score interval and the Clopper-Pearson interval are also compliant with this property. The practical import is that these intervals may be employed as significance tests, with identical results to the source test, and new tests may be derived by geometry.[9]
Wilson score interval with continuity correction
The Wilson interval may be modified by employing a continuity correction, in order to align the minimum coverage probability, rather than the average coverage probability, with the nominal value, [math]\displaystyle{ ~ 1 - \alpha ~. }[/math]
Just as the Wilson interval mirrors Pearson's chi-squared test, the Wilson interval with continuity correction mirrors the equivalent Yates' chi-squared test.
The following formulae for the lower and upper bounds of the Wilson score interval with continuity correction [math]\displaystyle{ ~ ( w_{cc}^- , w_{cc}^+ ) ~ }[/math] are derived from Newcombe (1998).[2]
- [math]\displaystyle{ \begin{align} w_{cc}^- &= \max\left\{ 0, \frac { 2n\hat{p} + z^2 - \left[\; z \; \sqrt{ z^2 - \frac{1}{n} + 4n\hat{p}(1 - \hat{p}) + (4\hat{p} - 2) \;} \; + \; 1 \;\right] \;} { 2(n + z^2) } \right\} \\ w_{cc}^+ &= \min\left\{ 1, \frac { 2n\hat{p} + z^2 + \left[\; z \; \sqrt{ z^2 - \frac{1}{n} + 4n\hat{p}(1 - \hat{p}) - (4\hat{p} - 2)\;} \; + \; 1 \; \right] \;} { 2(n + z^2) } \right\} \end{align} }[/math]
However, if p = 0 , [math]\displaystyle{ \; w_{cc}^- \; }[/math] must be taken as 0; or if p = 1 , then [math]\displaystyle{ \; w_{cc}^+ \; }[/math] is then 1.
Wallis (2021)[9] identifies a simpler method for computing continuity-corrected Wilson intervals that employs special functions. In Wallis' notation, for the lower bound, let [math]\displaystyle{ ~ \mathrm{WilsonLower}(\hat{p}, n, \alpha/2) = w^- ~, }[/math] where [math]\displaystyle{ \;\alpha\; }[/math] is the selected error level for [math]\displaystyle{ z }[/math]. Then [math]\displaystyle{ ~ w_{cc}^- = \mathrm{WilsonLower}(\max(\hat{p} - \tfrac{1}{2n}, 0), n, \alpha/2) ~. }[/math] This method has the advantage of being further decomposable.
Jeffreys interval
The Jeffreys interval has a Bayesian derivation, but good frequentist properties (outperforming most frequentist constructions). In particular, it has coverage properties that are similar to those of the Wilson interval, but it is one of the few intervals with the advantage of being equal-tailed (e.g., for a 95% confidence interval, the probabilities of the interval lying above or below the true value are both close to 2.5%). In contrast, the Wilson interval has a systematic bias such that it is centred too close to p = 0.5.[10]
The Jeffreys interval is the Bayesian credible interval obtained when using the non-informative Jeffreys prior for the binomial proportion p. The Jeffreys prior for this problem is a Beta distribution with parameters (1/2, 1/2), a conjugate prior. After observing x successes in n trials, the posterior distribution for p is a Beta distribution with parameters (x + 1/2, n – x + 1/2).
When x ≠0 and x ≠ n, the Jeffreys interval is taken to be the 100(1 – α)% equal-tailed posterior probability interval, i.e., the α / 2 and 1 – α / 2 quantiles of a Beta distribution with parameters (x + 1/2, n – x + 1/2).
In order to avoid the coverage probability tending to zero when p → 0 or 1, when x = 0 the upper limit is calculated as before but the lower limit is set to 0, and when x = n the lower limit is calculated as before but the upper limit is set to 1.[4]
Jeffreys' interval can also be thought of as a frequentist interval based on inverting the p-value from the G-test after applying the Yates correction to avoid a potentially-infinite value for the test statistic.
Clopper–Pearson interval
The Clopper–Pearson interval is an early and very common method for calculating binomial confidence intervals.[11] This is often called an 'exact' method, as it attains the nominal coverage level in an exact sense, meaning that the coverage level is never less than the nominal [math]\displaystyle{ 1 - \alpha }[/math].[2]
The Clopper–Pearson interval can be written as
- [math]\displaystyle{ S_{\le} \cap S_{\ge} }[/math]
or equivalently,
- [math]\displaystyle{ \left( \inf S_{\ge}\,,\, \sup S_{\le} \right) }[/math]
with
- [math]\displaystyle{ S_{\le} := \left\{ p \,\,\Big|\,\, P \left[ \operatorname{Bin}\left( n; p \right) \le x \right] \gt \frac{\alpha}{2} \right\} \text{ and } S_{\ge} := \left\{ p \,\,\Big|\,\, P \left[ \operatorname{Bin}\left( n; p \right) \ge x \right] \gt \frac{\alpha}{2} \right\}, }[/math]
where 0 ≤ x ≤ n is the number of successes observed in the sample and Bin(n; p) is a binomial random variable with n trials and probability of success p.
Equivalently we can say that the Clopper–Pearson interval is [math]\displaystyle{ \left(\frac{x}{n} - \varepsilon_1,\ \frac{x}{n} + \varepsilon_2\right) }[/math] with confidence level [math]\displaystyle{ 1 - \alpha }[/math] if [math]\displaystyle{ \varepsilon_i }[/math] is the infimum of those such that the following tests of hypothesis succeed with significance [math]\displaystyle{ \frac{\alpha}{2} }[/math]:
- H0: [math]\displaystyle{ p = \frac{x}{n} - \varepsilon_1 }[/math] with HA: [math]\displaystyle{ p \gt \frac{x}{n} - \varepsilon_1 }[/math]
- H0: [math]\displaystyle{ p = \frac{x}{n} + \varepsilon_2 }[/math] with HA: [math]\displaystyle{ p \lt \frac{x}{n} + \varepsilon_2 }[/math].
Because of a relationship between the binomial distribution and the beta distribution, the Clopper–Pearson interval is sometimes presented in an alternate format that uses quantiles from the beta distribution.[12]
- [math]\displaystyle{ B\left(\frac{\alpha}{2}; x , n - x + 1 \right) \lt p \lt B\left(1 - \frac{\alpha}{2}; x + 1, n - x\right) }[/math]
where x is the number of successes, n is the number of trials, and B(p; v,w) is the pth quantile from a beta distribution with shape parameters v and w.
Thus, [math]\displaystyle{ p_{\min} \lt p \lt p_{\max} }[/math], where:
- [math]\displaystyle{ \frac{\Gamma(n+1)}{\Gamma(x )\Gamma(n-x+1)}\int_0^{ p_{\min}} t^{x-1}(1-t)^{n-x}dt = \frac{\alpha}{2} }[/math]
- [math]\displaystyle{ \frac{\Gamma(n+1)}{\Gamma(x+1)\Gamma(n-x)}\int_0^{ p_{\max}} t^{x}(1-t)^{n-x-1}dt = 1-\frac{\alpha}{2} }[/math]
The binomial proportion confidence interval is then [math]\displaystyle{ ( p_{\min}, p_{\max}) }[/math], as follows from the relation between the Binomial distribution cumulative distribution function and the regularized incomplete beta function.
When [math]\displaystyle{ x }[/math] is either [math]\displaystyle{ 0 }[/math] or [math]\displaystyle{ n }[/math], closed-form expressions for the interval bounds are available: when [math]\displaystyle{ x = 0 }[/math] the interval is [math]\displaystyle{ \left(0,\, 1 - \left(\frac{\alpha}{2}\right)^\frac{1}{n} \right) }[/math] and when [math]\displaystyle{ x = n }[/math] it is [math]\displaystyle{ \left(\left(\frac{\alpha}{2}\right)^\frac{1}{n},\, 1\right) }[/math].[12]
The beta distribution is, in turn, related to the F-distribution so a third formulation of the Clopper–Pearson interval can be written using F quantiles:
- [math]\displaystyle{ \left( 1 + \frac{n - x+1}{(x ) \,F\!\left[\frac{\alpha}{2}; 2(x ), 2(n - x+1)\right]} \right)^{-1} \lt p \lt \left( 1 + \frac{n - x}{(x + 1)\,\,F\!\left[1 - \frac{\alpha}{2}; 2(x + 1), 2(n - x)\right]} \right)^{-1} }[/math]
where x is the number of successes, n is the number of trials, and F(c; d1, d2) is the c quantile from an F-distribution with d1 and d2 degrees of freedom.[13]
The Clopper–Pearson interval is an exact interval since it is based directly on the binomial distribution rather than any approximation to the binomial distribution. This interval never has less than the nominal coverage for any population proportion, but that means that it is usually conservative. For example, the true coverage rate of a 95% Clopper–Pearson interval may be well above 95%, depending on n and p.[4] Thus the interval may be wider than it needs to be to achieve 95% confidence, and wider than other intervals. In contrast, it is worth noting that other confidence interval may have coverage levels that are lower than the nominal [math]\displaystyle{ 1 - \alpha }[/math], i.e., the normal approximation (or "standard") interval, Wilson interval,[8] Agresti–Coull interval,[13] etc., with a nominal coverage of 95% may in fact cover less than 95%,[4] even for large sample sizes.[12]
The definition of the Clopper–Pearson interval can also be modified to obtain exact confidence intervals for different distributions. For instance, it can also be applied to the case where the samples are drawn without replacement from a population of a known size, instead of repeated draws of a binomial distribution. In this case, the underlying distribution would be the hypergeometric distribution.
The interval boundaries can be computed with numerical functions qbeta[14] in R and scipy.stats.beta.ppf[15] in Python.
from scipy.stats import beta k = 20 n = 400 alpha = 0.05 p_u, p_o = beta.ppf([alpha/2, 1 - alpha/2], [k, k + 1], [n - k + 1, n - k])
Agresti–Coull interval
The Agresti–Coull interval is also another approximate binomial confidence interval.[13]
Given [math]\displaystyle{ n_S }[/math] successes in [math]\displaystyle{ n }[/math] trials, define
- [math]\displaystyle{ \tilde{n} = n + z^2 }[/math]
and
- [math]\displaystyle{ \tilde{p} = \frac{1}{\tilde{n}}\left(n_S + \frac{z^2}{2}\right) }[/math]
Then, a confidence interval for [math]\displaystyle{ p }[/math] is given by
- [math]\displaystyle{ \tilde{p} \pm z \sqrt{\frac{\tilde{p}}{\tilde{n}}\left(1 - \tilde{p} \right)} }[/math]
where [math]\displaystyle{ z = \Phi^{-1}\!\left(1 - \frac{\alpha}{2}\!\right) }[/math] is the quantile of a standard normal distribution, as before (for example, a 95% confidence interval requires [math]\displaystyle{ \alpha = 0.05 }[/math], thereby producing [math]\displaystyle{ z = 1.96 }[/math]). According to Brown, Cai, and DasGupta,[4] taking [math]\displaystyle{ z = 2 }[/math] instead of 1.96 produces the "add 2 successes and 2 failures" interval previously described by Agresti and Coull.[13]
This interval can be summarised as employing the centre-point adjustment, [math]\displaystyle{ \tilde{p} }[/math], of the Wilson score interval, and then applying the Normal approximation to this point.[3][4]
- [math]\displaystyle{ \tilde{p} = \frac{\hat p+\frac{z^2}{2n}}{1+\frac{z^2}{n}} }[/math]
Arcsine transformation
The arcsine transformation has the effect of pulling out the ends of the distribution.[16] While it can stabilize the variance (and thus confidence intervals) of proportion data, its use has been criticized in several contexts.[17]
Let X be the number of successes in n trials and let p = X/n. The variance of p is
- [math]\displaystyle{ \operatorname{var}(p) = \frac{p (1 - p)}{n} . }[/math]
Using the arc sine transform, the variance of the arcsine of p1/2 is[18]
- [math]\displaystyle{ \operatorname{var}\left(\arcsin\sqrt{p}\right) \approx \frac{\operatorname{var}(p)}{4p (1 - p)} = \frac{p (1 - p)}{4n p(1 - p)} = \frac{1}{4n} . }[/math]
So, the confidence interval itself has the form
- [math]\displaystyle{ \left(\sin\left(\arcsin\sqrt{p} - \frac{z}{2\sqrt{n}}\right)\right)^2 \lt \theta \lt \left(\sin\left(\arcsin\sqrt{p} + \frac{z}{2\sqrt{n}}\right)\right)^2, }[/math]
where [math]\displaystyle{ z }[/math] is the [math]\displaystyle{ \scriptstyle 1 \,-\, \frac{\alpha}{2} }[/math] quantile of a standard normal distribution.
This method may be used to estimate the variance of p but its use is problematic when p is close to 0 or 1.
ta transform
Let p be the proportion of successes. For 0 ≤ a ≤ 2,
- [math]\displaystyle{ t_a = \log\left( \frac{p^a}{ (1 - p)^{2-a} } \right) = a \log(p) - (2-a) \log(1-p) }[/math]
This family is a generalisation of the logit transform which is a special case with a = 1 and can be used to transform a proportional data distribution to an approximately normal distribution. The parameter a has to be estimated for the data set.
Rule of three — for when no successes are observed
The rule of three is used to provide a simple way of stating an approximate 95% confidence interval for p, in the special case that no successes ([math]\displaystyle{ \hat p = 0 }[/math]) have been observed.[19] The interval is (0,3/n).
By symmetry, in the case of only successes ([math]\displaystyle{ \hat p = 1 }[/math]), the interval is (1 − 3/n,1).
Comparison and discussion
There are several research papers that compare these and other confidence intervals for the binomial proportion.[3][2][20][21] Both Agresti and Coull (1998)[13] and Ross (2003)[22] point out that exact methods such as the Clopper–Pearson interval may not work as well as certain approximations. The Normal approximation interval and its presentation in textbooks has been heavily criticised, with many statisticians advocating that it be not used.[4] The principal problems are overshoot (bounds exceed [0, 1]), zero-width intervals at [math]\displaystyle{ \hat p }[/math] = 0 and 1 (falsely implying certainty),[2] and overall inconsistency with significance testing.[3]
Of the approximations listed above, Wilson score interval methods (with or without continuity correction) have been shown to be the most accurate and the most robust,[3][4][2] though some prefer the Agresti–Coull approach for larger sample sizes.[4] Wilson and Clopper–Pearson methods obtain consistent results with source significance tests,[9] and this property is decisive for many researchers.
Many of these intervals can be calculated in R using packages like "binom".[23]
See also
- Binomial distribution
- Estimation theory
- Pseudocount
References
- ↑ Sullivan, Lisa (2017-10-27). "Confidence Intervals". http://sphweb.bumc.bu.edu/otlt/MPH-Modules/BS/BS704_Confidence_Intervals/.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 Newcombe, R. G. (1998). "Two-sided confidence intervals for the single proportion: comparison of seven methods". Statistics in Medicine 17 (8): 857–872. doi:10.1002/(SICI)1097-0258(19980430)17:8<857::AID-SIM777>3.0.CO;2-E. PMID 9595616.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 Wallis, Sean A. (2013). "Binomial confidence intervals and contingency tests: mathematical fundamentals and the evaluation of alternative methods". Journal of Quantitative Linguistics 20 (3): 178–208. doi:10.1080/09296174.2013.799918. http://www.ucl.ac.uk/english-usage/staff/sean/resources/binomialpoisson.pdf.
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 Brown, Lawrence D.; Cai, T. Tony; DasGupta, Anirban (2001). "Interval Estimation for a Binomial Proportion". Statistical Science 16 (2): 101–133. doi:10.1214/ss/1009213286.
- ↑ Laplace, Pierre Simon (1812) (in fr). Théorie analytique des probabilités. Ve. Courcier. pp. 283. https://archive.org/details/thorieanalytiqu00laplgoog.
- ↑ 6.0 6.1 Short, Michael (2021-11-08). "On binomial quantile and proportion bounds: With applications in engineering and informatics". Communications in Statistics - Theory and Methods 52 (12): 4183–4199. doi:10.1080/03610926.2021.1986540. ISSN 0361-0926.
- ↑ How to calculate the standard error of a proportion using weighted data?
- ↑ 8.0 8.1 Wilson, E. B. (1927). "Probable inference, the law of succession, and statistical inference". Journal of the American Statistical Association 22 (158): 209–212. doi:10.1080/01621459.1927.10502953.
- ↑ 9.0 9.1 9.2 9.3 Wallis, Sean A. (2021). Statistics in Corpus Linguistics - a new approach. New York: Routledge. ISBN 9781138589384. https://www.routledge.com/Statistics-in-Corpus-Linguistics-Research-A-New-Approach/Wallis/p/book/9781138589384.
- ↑ Cai, TT (2005). "One-sided confidence intervals in discrete distributions". Journal of Statistical Planning and Inference 131 (1): 63–88. doi:10.1016/j.jspi.2004.01.005.
- ↑ Clopper, C.; Pearson, E. S. (1934). "The use of confidence or fiducial limits illustrated in the case of the binomial". Biometrika 26 (4): 404–413. doi:10.1093/biomet/26.4.404.
- ↑ 12.0 12.1 12.2 Thulin, Måns (2014-01-01). "The cost of using exact confidence intervals for a binomial proportion" (in EN). Electronic Journal of Statistics 8 (1): 817–840. doi:10.1214/14-EJS909. ISSN 1935-7524.
- ↑ 13.0 13.1 13.2 13.3 13.4 Agresti, Alan; Coull, Brent A. (1998). "Approximate is better than 'exact' for interval estimation of binomial proportions". The American Statistician 52 (2): 119–126. doi:10.2307/2685469.
- ↑ "R: The Beta Distribution". https://stat.ethz.ch/R-manual/R-devel/library/stats/html/Beta.html.
- ↑ "scipy.stats.beta — SciPy v1.11.4 Manual". https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.beta.html.
- ↑ Holland, Steven. "Transformations of proportions and percentages". http://strata.uga.edu/8370/rtips/proportions.html.
- ↑ Warton, David I.; Hui, Francis K. C. (January 2011). "The arcsine is asinine: the analysis of proportions in ecology" (in en). Ecology 92 (1): 3–10. doi:10.1890/10-0340.1. ISSN 0012-9658. PMID 21560670. http://doi.wiley.com/10.1890/10-0340.1.
- ↑ Shao J (1998) Mathematical statistics. Springer. New York, New York, USA
- ↑ Steve Simon (2010) "Confidence interval with zero events", The Children's Mercy Hospital, Kansas City, Mo. (website: "Ask Professor Mean at Stats topics or Medical Research )
- ↑ Reiczigel, J (2003). "Confidence intervals for the binomial parameter: some new considerations". Statistics in Medicine 22 (4): 611–621. doi:10.1002/sim.1320. PMID 12590417. http://www.zoologia.hu/qp/Reiczigel_conf_int.pdf.
- ↑ Sauro J., Lewis J.R. (2005) "Comparison of Wald, Adj-Wald, Exact and Wilson intervals Calculator" . Proceedings of the Human Factors and Ergonomics Society, 49th Annual Meeting (HFES 2005), Orlando, FL, pp. 2100–2104
- ↑ Ross, T. D. (2003). "Accurate confidence intervals for binomial proportion and Poisson rate estimation". Computers in Biology and Medicine 33 (6): 509–531. doi:10.1016/S0010-4825(03)00019-2. PMID 12878234. https://zenodo.org/record/1259565.
- ↑ Dorai-Raj, Sundar (2022-05-02), binom: Binomial Confidence Intervals for Several Parameterizations, https://cran.r-project.org/web/packages/binom/index.html, retrieved 2023-12-02
 |