Clearance (pharmacology)

Short description: Pharmacokinetic measurement

In pharmacology, clearance ([math]\displaystyle{ Cl_{tot} }[/math]) is a pharmacokinetic parameter representing the efficiency of drug elimination. This is the rate of elimination of a substance divided by its concentration. The parameter also indicates the theoretical volume of plasma from which a substance would be completely removed per unit time. Usually, clearance is measured in L/h or mL/min. The quantity reflects the rate of drug elimination divided by plasma concentration. Excretion, on the other hand, is a measurement of the amount of a substance removed from the body per unit time (e.g., mg/min, μg/min, etc.). While clearance and excretion of a substance are related, they are not the same thing. The concept of clearance was described by Thomas Addis, a graduate of the University of Edinburgh Medical School.

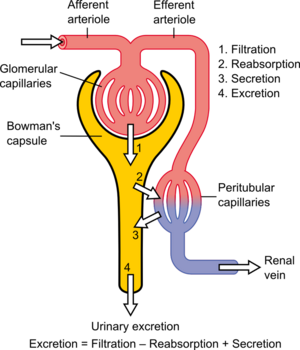
Substances in the body can be cleared by various organs, including the kidneys, liver, lungs, etc. Thus, total body clearance is equal to the sum clearance of the substance by each organ (e.g., renal clearance + hepatic clearance + lung clearance = total body clearance). For many drugs, however, clearance is solely a function of renal excretion. In these cases, clearance is almost synonymous with renal clearance or renal plasma clearance. Each substance has a specific clearance that depends on how the substance is handled by the nephron. Clearance is a function of 1) glomerular filtration, 2) secretion from the peritubular capillaries to the nephron, and 3) reabsorption from the nephron back to the peritubular capillaries. Clearance is variable in zero-order kinetics because a constant amount of the drug is eliminated per unit time, but it is constant in first-order kinetics, because the amount of drug eliminated per unit time changes with the concentration of drug in the blood.

Clearance can refer to the volume of plasma from which the substance is removed (i.e., cleared) per unit time or, in some cases, inter-compartmental clearances can be discussed when referring to redistribution between body compartments such as plasma, muscle, and fat.

Definition

Diagram showing the basic physiologic mechanisms of the kidney

The clearance of a substance is the volume of plasma that contains the same amount of the substance as has been removed from the plasma per unit time.

When referring to the function of the kidney, clearance is considered to be the amount of liquid filtered out of the blood that gets processed by the kidneys or the amount of blood cleaned per time because it has the units of a volumetric flow rate [ volume per unit time ]. However, it does not refer to a real value; "the kidney does not completely remove a substance from the total renal plasma flow." From a mass transfer perspective and physiologically, volumetric blood flow (to the dialysis machine and/or kidney) is only one of several factors that determine blood concentration and removal of a substance from the body. Other factors include the mass transfer coefficient, dialysate flow and dialysate recirculation flow for hemodialysis, and the glomerular filtration rate and the tubular reabsorption rate, for the kidney. A physiologic interpretation of clearance (at steady-state) is that clearance is a ratio of the mass generation and blood (or plasma) concentration.

Its definition follows from the differential equation that describes exponential decay and is used to model kidney function and hemodialysis machine function:

[math]\displaystyle{ V \frac{dC}{dt} = -K \cdot C + \dot{m} }[/math]

(1)

Where:

• [math]\displaystyle{ \dot{m} }[/math] is the mass generation rate of the substance - assumed to be a constant, i.e. not a function of time (equal to zero for foreign substances/drugs) [mmol/min] or [mol/s]
• t is dialysis time or time since injection of the substance/drug [min] or [s]
• V is the volume of distribution or total body water [L] or [m³]
• K is the clearance [mL/min] or [m³/s]
• C is the concentration [mmol/L] or [mol/m³] (in the United States often [mg/mL])

From the above definitions it follows that [math]\displaystyle{ \frac{dC}{dt} }[/math] is the first derivative of concentration with respect to time, i.e. the change in concentration with time.

It is derived from a mass balance.

Clearance of a substance is sometimes expressed as the inverse of the time constant that describes its removal rate from the body divided by its volume of distribution (or total body water).

In steady-state, it is defined as the mass generation rate of a substance (which equals the mass removal rate) divided by its concentration in the blood.

Clearance, half-life and distribution volume

There is an important relationship between clearance, elimination half-life and distribution volume. The elimination rate constant of a drug [math]\displaystyle{ K_{el} }[/math] is equivalent to total clearance divided by the distribution volume

[math]\displaystyle{ K_{el} = \dfrac{Cl_{tot}}{V_d} }[/math]

(note the usage of Cl and not Κ, not to confuse with [math]\displaystyle{ K_{el} }[/math]). But [math]\displaystyle{ K_{el} }[/math] is also equivalent to [math]\displaystyle{ \ln 2 }[/math] divided by elimination rate half-life [math]\displaystyle{ t_{1/2} }[/math], [math]\displaystyle{ K_{el} =\dfrac{\ln 2} {t_{1/2} } }[/math]. Thus, [math]\displaystyle{ Cl_{tot} = \dfrac{\ln2 \cdot V_d}{t_{1/2}} }[/math] . This means, for example, that an increase in total clearance results in a decrease in elimination rate half-life, provided distribution volume is constant. Derivation of these equations can be found in e.g. Rang and Dale's Pharmacology

Effect of plasma protein binding

For substances that exhibit substantial plasma protein binding, clearance is generally dependent on the total concentration (free + protein-bound) and not the free concentration.

Most plasma substances have primarily their free concentrations regulated, which thus remains the same, so extensive protein binding increases total plasma concentration (free + protein-bound). This decreases clearance compared to what would have been the case if the substance did not bind to protein. However, the mass removal rate is the same, because it depends only on concentration of free substance, and is independent on plasma protein binding, even with the fact that plasma proteins increase in concentration in the distal renal glomerulus as plasma is filtered into Bowman's capsule, because the relative increases in concentrations of substance-protein and non-occupied protein are equal and therefore give no net binding or dissociation of substances from plasma proteins, thus giving a constant plasma concentration of free substance throughout the glomerulus, which also would have been the case without any plasma protein binding.

In other sites than the kidneys, however, where clearance is made by membrane transport proteins rather than filtration, extensive plasma protein binding may increase clearance by keeping concentration of free substance fairly constant throughout the capillary bed, inhibiting a decrease in clearance caused by decreased concentration of free substance through the capillary.

Derivation of equation

Equation 1 is derived from a mass balance:

[math]\displaystyle{ \Delta m_\text{body}=(-\dot m_\text{out}+ \dot m_\text{in} +\dot m_\text{gen.})\Delta t }[/math]

(2)

where:

• [math]\displaystyle{ \Delta t }[/math] is a period of time
• [math]\displaystyle{ \Delta m_\text{body} }[/math] the change in mass of the toxin in the body during [math]\displaystyle{ \Delta t }[/math]
• [math]\displaystyle{ \dot m_\text{in} }[/math] is the toxin intake rate
• [math]\displaystyle{ \dot m_\text{out} }[/math] is the toxin removal rate
• [math]\displaystyle{ \dot m_\text{gen.} }[/math] is the toxin generation rate

In words, the above equation states:

The change in the mass of a toxin within the body ([math]\displaystyle{ \Delta m }[/math]) during some time [math]\displaystyle{ \Delta t }[/math] is equal to the toxin intake plus the toxin generation minus the toxin removal.

Since

[math]\displaystyle{ m_\text{body} = C \cdot V }[/math]

(3)

and

[math]\displaystyle{ \dot m_\text{out}=K \cdot C }[/math]

(4)

Equation A1 can be rewritten as:

[math]\displaystyle{ \Delta (C \cdot V) = \left(-K \cdot C+ \dot m_\text{in} +\dot m_\text{gen.}\right)\Delta t }[/math]

(5)

If one lumps the in and gen. terms together, i.e. [math]\displaystyle{ \dot m=\dot m_\text{in} +\dot m_\text{gen.} }[/math] and divides by [math]\displaystyle{ \Delta t }[/math] the result is a difference equation:

[math]\displaystyle{ \frac{\Delta (C \cdot V)}{\Delta t} = -K \cdot C + \dot{m} }[/math]

(6)

If one applies the limit [math]\displaystyle{ \Delta t \to 0 }[/math] one obtains a differential equation:

[math]\displaystyle{ \frac{d(C \cdot V)}{dt}= -K \cdot C + \dot{m} }[/math]

(7)

Using the product rule this can be rewritten as:

[math]\displaystyle{ C \frac{dV}{dt}+V \frac{dC}{dt} = -K \cdot C + \dot{m} }[/math]

(8)

If one assumes that the volume change is not significant, i.e. [math]\displaystyle{ C \frac{dV}{dt}=0 }[/math], the result is Equation 1:

Solution to the differential equation

The general solution of the above differential equation (1) is:

[math]\displaystyle{ C = \frac{\dot{m}}{K} + \left(C_{o}-\frac{\dot{m}}{K}\right) e^{-\frac{K \cdot t}{V}} }[/math]

(9)

Where:

• C_o is the concentration at the beginning of dialysis or the initial concentration of the substance/drug (after it has distributed) [mmol/L] or [mol/m³]
• e is the base of the natural logarithm

Steady-state solution

The solution to the above differential equation (9) at time infinity (steady state) is:

[math]\displaystyle{ C_{\infty} = \frac {\dot{m}}{K} }[/math]

(10a)

The above equation (10a) can be rewritten as:

[math]\displaystyle{ K = \frac {\dot{m}}{C_{\infty}} }[/math]

(10b)

The above equation (10b) makes clear the relationship between mass removal and clearance. It states that (with a constant mass generation) the concentration and clearance vary inversely with one another. If applied to creatinine (i.e. creatinine clearance), it follows from the equation that if the serum creatinine doubles the clearance halves and that if the serum creatinine quadruples the clearance is quartered.

Measurement of renal clearance

Renal clearance can be measured with a timed collection of urine and an analysis of its composition with the aid of the following equation (which follows directly from the derivation of (10b)):

[math]\displaystyle{ K = \frac {C_U \cdot Q}{C_B} }[/math]

(11)

Where:

• K is the clearance [mL/min]
• C_U is the urine concentration [mmol/L] (in the USA often [mg/mL])
• Q is the urine flow (volume/time) [mL/min] (often [mL/24 h])
• C_B is the plasma concentration [mmol/L] (in the USA often [mg/mL])

When the substance "C" is creatinine, an endogenous chemical that is excreted only by filtration, the clearance is an approximation of the glomerular filtration rate. Inulin clearance is less commonly used to precisely determine glomerular filtration rate.

Note - the above equation (11) is valid only for the steady-state condition. If the substance being cleared is not at a constant plasma concentration (i.e. not at steady-state) K must be obtained from the (full) solution of the differential equation (9).

Further reading

• "Estimation of biliary excretion of foreign compounds using properties of molecular structure". The AAPS Journal 16 (1): 65–78. January 2014. doi:10.1208/s12248-013-9541-z. PMID 24202722. 

de:Clearance (Medizin)