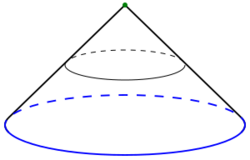
Cone (topology)

Cone of a circle. The original space X is in blue, and the collapsed end point v is in green.

In topology, especially algebraic topology, the cone of a topological space [math]\displaystyle{ X }[/math] is intuitively obtained by stretching X into a cylinder and then collapsing one of its end faces to a point. The cone of X is denoted by [math]\displaystyle{ CX }[/math] or by [math]\displaystyle{ \operatorname{cone}(X) }[/math].

Definitions

Formally, the cone of X is defined as:

[math]\displaystyle{ CX = (X \times [0,1])\cup_p v\ =\ \varinjlim \bigl( (X \times [0,1]) \hookleftarrow (X\times \{0\}) \xrightarrow{p} v\bigr), }[/math]

where [math]\displaystyle{ v }[/math] is a point (called the vertex of the cone) and [math]\displaystyle{ p }[/math] is the projection to that point. In other words, it is the result of attaching the cylinder [math]\displaystyle{ X \times [0,1] }[/math] by its face [math]\displaystyle{ X\times\{0\} }[/math] to a point [math]\displaystyle{ v }[/math] along the projection [math]\displaystyle{ p: \bigl( X\times\{0\} \bigr)\to v }[/math].

If [math]\displaystyle{ X }[/math] is a non-empty compact subspace of Euclidean space, the cone on [math]\displaystyle{ X }[/math] is homeomorphic to the union of segments from [math]\displaystyle{ X }[/math] to any fixed point [math]\displaystyle{ v \not\in X }[/math] such that these segments intersect only in [math]\displaystyle{ v }[/math] itself. That is, the topological cone agrees with the geometric cone for compact spaces when the latter is defined. However, the topological cone construction is more general.

The cone is a special case of a join: [math]\displaystyle{ CX \simeq X\star \{v\} = }[/math] the join of [math]\displaystyle{ X }[/math] with a single point [math]\displaystyle{ v\not\in X }[/math].

Examples

Here we often use a geometric cone ([math]\displaystyle{ C X }[/math] where [math]\displaystyle{ X }[/math] is a non-empty compact subspace of Euclidean space). The considered spaces are compact, so we get the same result up to homeomorphism.

• The cone over a point p of the real line is a line-segment in [math]\displaystyle{ \mathbb{R}^2 }[/math], [math]\displaystyle{ \{p\} \times [0,1] }[/math].
• The cone over two points {0, 1} is a "V" shape with endpoints at {0} and {1}.
• The cone over a closed interval I of the real line is a filled-in triangle (with one of the edges being I), otherwise known as a 2-simplex (see the final example).
• The cone over a polygon P is a pyramid with base P.
• The cone over a disk is the solid cone of classical geometry (hence the concept's name).
• The cone over a circle given by

[math]\displaystyle{ \{(x,y,z) \in \R^3 \mid x^2 + y^2 = 1 \mbox{ and } z=0\} }[/math]

is the curved surface of the solid cone:

[math]\displaystyle{ \{(x,y,z) \in \R^3 \mid x^2 + y^2 = (z-1)^2 \mbox{ and } 0\leq z\leq 1\}. }[/math]

This in turn is homeomorphic to the closed disc.

More general examples:

• The cone over an n-sphere is homeomorphic to the closed (n + 1)-ball.
• The cone over an n-ball is also homeomorphic to the closed (n + 1)-ball.
• The cone over an n-simplex is an (n + 1)-simplex.

Properties

All cones are path-connected since every point can be connected to the vertex point. Furthermore, every cone is contractible to the vertex point by the homotopy

[math]\displaystyle{ h_t(x,s) = (x, (1-t)s) }[/math].

The cone is used in algebraic topology precisely because it embeds a space as a subspace of a contractible space.

When X is compact and Hausdorff (essentially, when X can be embedded in Euclidean space), then the cone [math]\displaystyle{ CX }[/math] can be visualized as the collection of lines joining every point of X to a single point. However, this picture fails when X is not compact or not Hausdorff, as generally the quotient topology on [math]\displaystyle{ CX }[/math] will be finer than the set of lines joining X to a point.

Cone functor

The map [math]\displaystyle{ X\mapsto CX }[/math] induces a functor [math]\displaystyle{ C\colon \mathbf{Top}\to\mathbf{Top} }[/math] on the category of topological spaces Top. If [math]\displaystyle{ f \colon X \to Y }[/math] is a continuous map, then [math]\displaystyle{ Cf \colon CX \to CY }[/math] is defined by

[math]\displaystyle{ (Cf)([x,t])=[f(x),t] }[/math],

where square brackets denote equivalence classes.

Reduced cone

If [math]\displaystyle{ (X,x_0) }[/math] is a pointed space, there is a related construction, the reduced cone, given by

[math]\displaystyle{ (X\times [0,1]) / (X\times \left\{0\right\} \cup\left\{x_0\right\}\times [0,1]) }[/math]

where we take the basepoint of the reduced cone to be the equivalence class of [math]\displaystyle{ (x_0,0) }[/math]. With this definition, the natural inclusion [math]\displaystyle{ x\mapsto (x,1) }[/math] becomes a based map. This construction also gives a functor, from the category of pointed spaces to itself.

See also

• Cone (disambiguation)
• Suspension (topology)
• Desuspension
• Mapping cone (topology)
• Join (topology)

References

• Allen Hatcher, Algebraic topology. Cambridge University Press, Cambridge, 2002. xii+544 pp. ISBN:0-521-79160-X and ISBN:0-521-79540-0
• "Cone". http://planetmath.org/?op=getobj&from=objects&id={{{id}}}.