Conjugate gradient method

Short description: Mathematical optimization algorithm

A comparison of the convergence of gradient descent with optimal step size (in green) and conjugate vector (in red) for minimizing a quadratic function associated with a given linear system. Conjugate gradient, assuming exact arithmetic, converges in at most n steps, where n is the size of the matrix of the system (here n = 2).

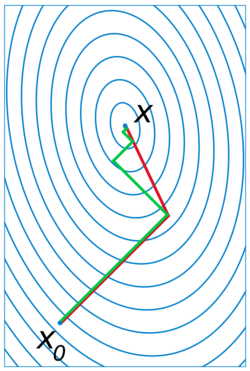
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-definite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems.

The conjugate gradient method can also be used to solve unconstrained optimization problems such as energy minimization. It is commonly attributed to Magnus Hestenes and Eduard Stiefel, who programmed it on the Z4, and extensively researched it.

The biconjugate gradient method provides a generalization to non-symmetric matrices. Various nonlinear conjugate gradient methods seek minima of nonlinear optimization problems.

Description of the problem addressed by conjugate gradients

Suppose we want to solve the system of linear equations

[math]\displaystyle{ \mathbf{A}\mathbf{x} = \mathbf{b} }[/math]

for the vector [math]\displaystyle{ \mathbf{x} }[/math], where the known [math]\displaystyle{ n \times n }[/math] matrix [math]\displaystyle{ \mathbf{A} }[/math] is symmetric (i.e., A^T = A), positive-definite (i.e. x^TAx > 0 for all non-zero vectors [math]\displaystyle{ \mathbf{x} }[/math] in Rⁿ), and real, and [math]\displaystyle{ \mathbf{b} }[/math] is known as well. We denote the unique solution of this system by [math]\displaystyle{ \mathbf{x}_* }[/math].

Derivation as a direct method

The conjugate gradient method can be derived from several different perspectives, including specialization of the conjugate direction method for optimization, and variation of the Arnoldi/Lanczos iteration for eigenvalue problems. Despite differences in their approaches, these derivations share a common topic—proving the orthogonality of the residuals and conjugacy of the search directions. These two properties are crucial to developing the well-known succinct formulation of the method.

We say that two non-zero vectors u and v are conjugate (with respect to [math]\displaystyle{ \mathbf{A} }[/math]) if

[math]\displaystyle{ \mathbf{u}^\mathsf{T} \mathbf{A} \mathbf{v} = 0. }[/math]

Since [math]\displaystyle{ \mathbf{A} }[/math] is symmetric and positive-definite, the left-hand side defines an inner product

[math]\displaystyle{ \mathbf{u}^\mathsf{T} \mathbf{A} \mathbf{v} = \langle \mathbf{u}, \mathbf{v} \rangle_\mathbf{A} := \langle \mathbf{A} \mathbf{u}, \mathbf{v}\rangle = \langle \mathbf{u}, \mathbf{A}^\mathsf{T} \mathbf{v}\rangle = \langle \mathbf{u}, \mathbf{A}\mathbf{v}\rangle. }[/math]

Two vectors are conjugate if and only if they are orthogonal with respect to this inner product. Being conjugate is a symmetric relation: if [math]\displaystyle{ \mathbf{u} }[/math] is conjugate to [math]\displaystyle{ \mathbf{v} }[/math], then [math]\displaystyle{ \mathbf{v} }[/math] is conjugate to [math]\displaystyle{ \mathbf{u} }[/math]. Suppose that

[math]\displaystyle{ P = \{ \mathbf{p}_1, \dots, \mathbf{p}_n \} }[/math]

is a set of [math]\displaystyle{ n }[/math] mutually conjugate vectors with respect to [math]\displaystyle{ \mathbf{A} }[/math], i.e. [math]\displaystyle{ \mathbf{p}_i^\mathsf{T} \mathbf{A} \mathbf{p}_j = 0 }[/math] for all [math]\displaystyle{ i \neq j }[/math]. Then [math]\displaystyle{ P }[/math] forms a basis for [math]\displaystyle{ \mathbb{R}^n }[/math], and we may express the solution [math]\displaystyle{ \mathbf{x}_* }[/math] of [math]\displaystyle{ \mathbf{Ax} = \mathbf{b} }[/math] in this basis:

[math]\displaystyle{ \mathbf{x}_* = \sum^{n}_{i=1} \alpha_i \mathbf{p}_i \Rightarrow \mathbf{A} \mathbf{x}_* = \sum^{n}_{i=1} \alpha_i \mathbf{A} \mathbf{p}_i. }[/math]

Left-multiplying the problem [math]\displaystyle{ \mathbf{Ax} = \mathbf{b} }[/math] with the vector [math]\displaystyle{ \mathbf{p}_k^\mathsf{T} }[/math] yields

[math]\displaystyle{ \mathbf{p}_k^\mathsf{T} \mathbf{b} = \mathbf{p}_k^\mathsf{T} \mathbf{A} \mathbf{x}_* = \sum^{n}_{i=1} \alpha_i \mathbf{p}_k^\mathsf{T} \mathbf{A} \mathbf{p}_i = \sum^{n}_{i=1} \alpha_i \left \langle \mathbf{p}_k, \mathbf{p}_i \right \rangle_{\mathbf{A}} = \alpha_k \left \langle \mathbf{p}_k, \mathbf{p}_k \right \rangle_{\mathbf{A}} }[/math]

and so

[math]\displaystyle{ \alpha_k = \frac{\langle \mathbf{p}_k, \mathbf{b} \rangle}{\langle \mathbf{p}_k, \mathbf{p}_k \rangle_\mathbf{A}}. }[/math]

This gives the following method for solving the equation Ax = b: find a sequence of [math]\displaystyle{ n }[/math] conjugate directions, and then compute the coefficients [math]\displaystyle{ \alpha_k }[/math].

As an iterative method

If we choose the conjugate vectors [math]\displaystyle{ \mathbf{p}_k }[/math] carefully, then we may not need all of them to obtain a good approximation to the solution [math]\displaystyle{ \mathbf{x}_* }[/math]. So, we want to regard the conjugate gradient method as an iterative method. This also allows us to approximately solve systems where n is so large that the direct method would take too much time.

We denote the initial guess for x_∗ by x₀ (we can assume without loss of generality that x₀ = 0, otherwise consider the system Az = b − Ax₀ instead). Starting with x₀ we search for the solution and in each iteration we need a metric to tell us whether we are closer to the solution x_∗ (that is unknown to us). This metric comes from the fact that the solution x_∗ is also the unique minimizer of the following quadratic function

[math]\displaystyle{ f(\mathbf{x}) = \tfrac12 \mathbf{x}^\mathsf{T} \mathbf{A}\mathbf{x} - \mathbf{x}^\mathsf{T} \mathbf{b}, \qquad \mathbf{x}\in\mathbf{R}^n \,. }[/math]

The existence of a unique minimizer is apparent as its Hessian matrix of second derivatives is symmetric positive-definite

[math]\displaystyle{ \mathbf{H}(f(\mathbf{x})) = \mathbf{A} \,, }[/math]

and that the minimizer (use Df(x)=0) solves the initial problem follows from its first derivative

[math]\displaystyle{ \nabla f(\mathbf{x}) = \mathbf{A} \mathbf{x} - \mathbf{b} \,. }[/math]

This suggests taking the first basis vector p₀ to be the negative of the gradient of f at x = x₀. The gradient of f equals Ax − b. Starting with an initial guess x₀, this means we take p₀ = b − Ax₀. The other vectors in the basis will be conjugate to the gradient, hence the name conjugate gradient method. Note that p₀ is also the residual provided by this initial step of the algorithm.

Let r_k be the residual at the kth step:

[math]\displaystyle{ \mathbf{r}_k = \mathbf{b} - \mathbf{Ax}_k. }[/math]

As observed above, [math]\displaystyle{ \mathbf{r}_k }[/math] is the negative gradient of [math]\displaystyle{ f }[/math] at [math]\displaystyle{ \mathbf{x}_k }[/math], so the gradient descent method would require to move in the direction r_k. Here, however, we insist that the directions [math]\displaystyle{ \mathbf{p}_k }[/math] must be conjugate to each other. A practical way to enforce this is by requiring that the next search direction be built out of the current residual and all previous search directions. The conjugation constraint is an orthonormal-type constraint and hence the algorithm can be viewed as an example of Gram-Schmidt orthonormalization. This gives the following expression:

[math]\displaystyle{ \mathbf{p}_{k} = \mathbf{r}_{k} - \sum_{i \lt k}\frac{\mathbf{p}_i^\mathsf{T} \mathbf{A} \mathbf{r}_{k}}{\mathbf{p}_i^\mathsf{T}\mathbf{A} \mathbf{p}_i} \mathbf{p}_i }[/math]

(see the picture at the top of the article for the effect of the conjugacy constraint on convergence). Following this direction, the next optimal location is given by

[math]\displaystyle{ \mathbf{x}_{k+1} = \mathbf{x}_k + \alpha_k \mathbf{p}_k }[/math]

with

[math]\displaystyle{ \alpha_{k} = \frac{\mathbf{p}_k^\mathsf{T} (\mathbf{b} - \mathbf{Ax}_k )}{\mathbf{p}_k^\mathsf{T} \mathbf{A} \mathbf{p}_k} = \frac{\mathbf{p}_{k}^\mathsf{T} \mathbf{r}_{k}}{\mathbf{p}_{k}^\mathsf{T} \mathbf{A} \mathbf{p}_{k}}, }[/math]

where the last equality follows from the definition of [math]\displaystyle{ \mathbf{r}_k }[/math] . The expression for [math]\displaystyle{ \alpha_k }[/math] can be derived if one substitutes the expression for x_k+1 into f and minimizing it with respect to [math]\displaystyle{ \alpha_k }[/math]

[math]\displaystyle{ \begin{align} f(\mathbf{x}_{k+1}) &= f(\mathbf{x}_k + \alpha_k \mathbf{p}_k) =: g(\alpha_k) \\ g'(\alpha_k) &\overset{!}{=} 0 \quad \Rightarrow \quad \alpha_{k} = \frac{\mathbf{p}_k^\mathsf{T} (\mathbf{b} - \mathbf{Ax}_k)}{\mathbf{p}_k^\mathsf{T} \mathbf{A} \mathbf{p}_k} \,. \end{align} }[/math]

The resulting algorithm

The above algorithm gives the most straightforward explanation of the conjugate gradient method. Seemingly, the algorithm as stated requires storage of all previous searching directions and residue vectors, as well as many matrix–vector multiplications, and thus can be computationally expensive. However, a closer analysis of the algorithm shows that [math]\displaystyle{ \mathbf{r}_i }[/math] is orthogonal to [math]\displaystyle{ \mathbf{r}_j }[/math], i.e. [math]\displaystyle{ \mathbf{r}_i^\mathsf{T} \mathbf{r}_j=0 }[/math] , for i ≠ j. And [math]\displaystyle{ \mathbf{p}_i }[/math]is [math]\displaystyle{ \mathbf{A} }[/math]-orthogonal to [math]\displaystyle{ \mathbf{p}_j }[/math] , i.e. [math]\displaystyle{ \mathbf{p}_i^\mathsf{T} \mathbf{A} \mathbf{p}_j=0 }[/math] , for [math]\displaystyle{ i \neq j }[/math]. This can be regarded that as the algorithm progresses, [math]\displaystyle{ \mathbf{p}_i }[/math] and [math]\displaystyle{ \mathbf{r}_i }[/math] span the same Krylov subspace. Where [math]\displaystyle{ \mathbf{r}_i }[/math] form the orthogonal basis with respect to the standard inner product, and [math]\displaystyle{ \mathbf{p}_i }[/math] form the orthogonal basis with respect to the inner product induced by [math]\displaystyle{ \mathbf{A} }[/math]. Therefore, [math]\displaystyle{ \mathbf{x}_k }[/math] can be regarded as the projection of [math]\displaystyle{ \mathbf{x} }[/math] on the Krylov subspace.

That is, if the CG method starts with [math]\displaystyle{ \mathbf{x}_0 = 0 }[/math], then[math]\displaystyle{ x_k = \mathrm{argmin}_{y \in \mathbb{R}^n} {\left\{(x-y)^{\top} A(x-y)^T: y \in \operatorname{span}\left\{b, A b, \ldots, A^{k-1} b\right\}\right\}} }[/math]The algorithm is detailed below for solving [math]\displaystyle{ \mathbf{A} \mathbf{x}= \mathbf{b} }[/math] where [math]\displaystyle{ \mathbf{A} }[/math] is a real, symmetric, positive-definite matrix. The input vector [math]\displaystyle{ \mathbf{x}_0 }[/math] can be an approximate initial solution or 0. It is a different formulation of the exact procedure described above.

[math]\displaystyle{ \begin{align} & \mathbf{r}_0 := \mathbf{b} - \mathbf{A x}_0 \\ & \hbox{if } \mathbf{r}_{0} \text{ is sufficiently small, then return } \mathbf{x}_{0} \text{ as the result}\\ & \mathbf{p}_0 := \mathbf{r}_0 \\ & k := 0 \\ & \text{repeat} \\ & \qquad \alpha_k := \frac{\mathbf{r}_k^\mathsf{T} \mathbf{r}_k}{\mathbf{p}_k^\mathsf{T} \mathbf{A p}_k} \\ & \qquad \mathbf{x}_{k+1} := \mathbf{x}_k + \alpha_k \mathbf{p}_k \\ & \qquad \mathbf{r}_{k+1} := \mathbf{r}_k - \alpha_k \mathbf{A p}_k \\ & \qquad \hbox{if } \mathbf{r}_{k+1} \text{ is sufficiently small, then exit loop} \\ & \qquad \beta_k := \frac{\mathbf{r}_{k+1}^\mathsf{T} \mathbf{r}_{k+1}}{\mathbf{r}_k^\mathsf{T} \mathbf{r}_k} \\ & \qquad \mathbf{p}_{k+1} := \mathbf{r}_{k+1} + \beta_k \mathbf{p}_k \\ & \qquad k := k + 1 \\ & \text{end repeat} \\ & \text{return } \mathbf{x}_{k+1} \text{ as the result} \end{align} }[/math]

This is the most commonly used algorithm. The same formula for β_k is also used in the Fletcher–Reeves nonlinear conjugate gradient method.

Restarts

We note that [math]\displaystyle{ \mathbf{x}_{1} }[/math] is computed by the gradient descent method applied to [math]\displaystyle{ \mathbf{x}_{0} }[/math]. Setting [math]\displaystyle{ \beta_{k}=0 }[/math] would similarly make [math]\displaystyle{ \mathbf{x}_{k+1} }[/math] computed by the gradient descent method from [math]\displaystyle{ \mathbf{x}_{k} }[/math], i.e., can be used as a simple implementation of a restart of the conjugate gradient iterations. Restarts could slow down convergence, but may improve stability if the conjugate gradient method misbehaves, e.g., due to round-off error.

Explicit residual calculation

The formulas [math]\displaystyle{ \mathbf{x}_{k+1} := \mathbf{x}_k + \alpha_k \mathbf{p}_k }[/math] and [math]\displaystyle{ \mathbf{r}_k := \mathbf{b} - \mathbf{A x}_k }[/math], which both hold in exact arithmetic, make the formulas [math]\displaystyle{ \mathbf{r}_{k+1} := \mathbf{r}_k - \alpha_k \mathbf{A p}_k }[/math] and [math]\displaystyle{ \mathbf{r}_{k+1} := \mathbf{b} - \mathbf{A x}_{k+1} }[/math] mathematically equivalent. The former is used in the algorithm to avoid an extra multiplication by [math]\displaystyle{ \mathbf{A} }[/math] since the vector [math]\displaystyle{ \mathbf{A p}_k }[/math] is already computed to evaluate [math]\displaystyle{ \alpha_k }[/math]. The latter may be more accurate, substituting the explicit calculation [math]\displaystyle{ \mathbf{r}_{k+1} := \mathbf{b} - \mathbf{A x}_{k+1} }[/math] for the implicit one by the recursion subject to round-off error accumulation, and is thus recommended for an occasional evaluation.

A norm of the residual is typically used for stopping criteria. The norm of the explicit residual [math]\displaystyle{ \mathbf{r}_{k+1} := \mathbf{b} - \mathbf{A x}_{k+1} }[/math] provides a guaranteed level of accuracy both in exact arithmetic and in the presence of the rounding errors, where convergence naturally stagnates. In contrast, the implicit residual [math]\displaystyle{ \mathbf{r}_{k+1} := \mathbf{r}_k - \alpha_k \mathbf{A p}_k }[/math] is known to keep getting smaller in amplitude well below the level of rounding errors and thus cannot be used to determine the stagnation of convergence.

Computation of alpha and beta

In the algorithm, α_k is chosen such that [math]\displaystyle{ \mathbf{r}_{k+1} }[/math] is orthogonal to [math]\displaystyle{ \mathbf{r}_{k} }[/math]. The denominator is simplified from

[math]\displaystyle{ \alpha_k = \frac{\mathbf{r}_{k}^\mathsf{T} \mathbf{r}_{k}}{\mathbf{r}_{k}^\mathsf{T} \mathbf{A} \mathbf{p}_k} = \frac{\mathbf{r}_k^\mathsf{T} \mathbf{r}_k}{\mathbf{p}_k^\mathsf{T} \mathbf{A p}_k} }[/math]

since [math]\displaystyle{ \mathbf{r}_{k+1} = \mathbf{p}_{k+1}-\mathbf{\beta}_{k}\mathbf{p}_{k} }[/math]. The β_k is chosen such that [math]\displaystyle{ \mathbf{p}_{k+1} }[/math] is conjugate to [math]\displaystyle{ \mathbf{p}_{k} }[/math]. Initially, β_k is

[math]\displaystyle{ \beta_k = - \frac{\mathbf{r}_{k+1}^\mathsf{T} \mathbf{A} \mathbf{p}_k}{\mathbf{p}_k^\mathsf{T} \mathbf{A} \mathbf{p}_k} }[/math]

using

[math]\displaystyle{ \mathbf{r}_{k+1} = \mathbf{r}_{k} - \alpha_{k} \mathbf{A} \mathbf{p}_{k} }[/math]

and equivalently

[math]\displaystyle{ \mathbf{A} \mathbf{p}_{k} = \frac{1}{\alpha_{k}} (\mathbf{r}_{k} - \mathbf{r}_{k+1}), }[/math]

the numerator of β_k is rewritten as

[math]\displaystyle{ \mathbf{r}_{k+1}^\mathsf{T} \mathbf{A} \mathbf{p}_k = \frac{1}{\alpha_k} \mathbf{r}_{k+1}^\mathsf{T} (\mathbf{r}_k - \mathbf{r}_{k+1}) = - \frac{1}{\alpha_k} \mathbf{r}_{k+1}^\mathsf{T} \mathbf{r}_{k+1} }[/math]

because [math]\displaystyle{ \mathbf{r}_{k+1} }[/math] and [math]\displaystyle{ \mathbf{r}_{k} }[/math] are orthogonal by design. The denominator is rewritten as

[math]\displaystyle{ \mathbf{p}_k^\mathsf{T} \mathbf{A} \mathbf{p}_k = (\mathbf{r}_k + \beta_{k-1} \mathbf{p}_{k-1})^\mathsf{T} \mathbf{A} \mathbf{p}_k = \frac{1}{\alpha_k} \mathbf{r}_k^\mathsf{T} (\mathbf{r}_k - \mathbf{r}_{k+1}) = \frac{1}{\alpha_k} \mathbf{r}_k^\mathsf{T} \mathbf{r}_k }[/math]

using that the search directions p_k are conjugated and again that the residuals are orthogonal. This gives the β in the algorithm after cancelling α_k.

Example code in Julia (programming language)

"""
    conjugate_gradient!(A, b, x)

Return the solution to `A * x = b` using the conjugate gradient method.
"""
function conjugate_gradient!(
    A::AbstractMatrix, b::AbstractVector, x::AbstractVector; tol=eps(eltype(b))
)
    # Initialize residual vector
    residual = b - A * x
    # Initialize search direction vector
    search_direction = residual
    # Compute initial squared residual norm
    old_sqr_resid_norm = residual' * residual

    # Iterate until convergence
    while old_sqr_resid_norm > tol
        A_search_direction = A * search_direction
        step_size = old_sqr_resid_norm^2 / (search_direction' * A_search_direction)
        # Update solution
        @. x = x + step_size * search_direction
        # Update residual
        @. residual = residual - step_size * A_search_direction
        new_sqr_resid_norm = dot(residual, residual)
        
        # Update search direction vector
        @. search_direction = residual + 
            (new_sqr_resid_norm / old_sqr_resid_norm)^2 * search_direction
        # Update squared residual norm for next iteration
        old_sqr_resid_norm = new_sqr_resid_norm
    end
    return x
end

Numerical example

Consider the linear system Ax = b given by

[math]\displaystyle{ \mathbf{A} \mathbf{x}= \begin{bmatrix} 4 & 1 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}, }[/math]

we will perform two steps of the conjugate gradient method beginning with the initial guess

[math]\displaystyle{ \mathbf{x}_0 = \begin{bmatrix} 2 \\ 1 \end{bmatrix} }[/math]

in order to find an approximate solution to the system.

Solution

For reference, the exact solution is

[math]\displaystyle{ \mathbf{x} = \begin{bmatrix} \frac{1}{11} \\\\ \frac{7}{11} \end{bmatrix} \approx \begin{bmatrix} 0.0909 \\\\ 0.6364 \end{bmatrix} }[/math]

Our first step is to calculate the residual vector r₀ associated with x₀. This residual is computed from the formula r₀ = b - Ax₀, and in our case is equal to

[math]\displaystyle{ \mathbf{r}_0 = \begin{bmatrix} 1 \\ 2 \end{bmatrix} - \begin{bmatrix} 4 & 1 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} 2 \\ 1 \end{bmatrix} = \begin{bmatrix}-8 \\ -3 \end{bmatrix} = \mathbf{p}_0. }[/math]

Since this is the first iteration, we will use the residual vector r₀ as our initial search direction p₀; the method of selecting p_k will change in further iterations.

We now compute the scalar α₀ using the relationship

[math]\displaystyle{ \alpha_0 = \frac{\mathbf{r}_0^\mathsf{T} \mathbf{r}_0}{\mathbf{p}_0^\mathsf{T} \mathbf{A p}_0} = \frac{\begin{bmatrix} -8 & -3 \end{bmatrix} \begin{bmatrix} -8 \\ -3 \end{bmatrix}}{ \begin{bmatrix} -8 & -3 \end{bmatrix} \begin{bmatrix} 4 & 1 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} -8 \\ -3 \end{bmatrix} } =\frac{73}{331}\approx0.2205 }[/math]

We can now compute x₁ using the formula

[math]\displaystyle{ \mathbf{x}_1 = \mathbf{x}_0 + \alpha_0\mathbf{p}_0 = \begin{bmatrix} 2 \\ 1 \end{bmatrix} + \frac{73}{331} \begin{bmatrix} -8 \\ -3 \end{bmatrix} \approx \begin{bmatrix} 0.2356 \\ 0.3384 \end{bmatrix}. }[/math]

This result completes the first iteration, the result being an "improved" approximate solution to the system, x₁. We may now move on and compute the next residual vector r₁ using the formula

[math]\displaystyle{ \mathbf{r}_1 = \mathbf{r}_0 - \alpha_0 \mathbf{A} \mathbf{p}_0 = \begin{bmatrix} -8 \\ -3 \end{bmatrix} - \frac{73}{331} \begin{bmatrix} 4 & 1 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} -8 \\ -3 \end{bmatrix} \approx \begin{bmatrix} -0.2810 \\ 0.7492 \end{bmatrix}. }[/math]

Our next step in the process is to compute the scalar β₀ that will eventually be used to determine the next search direction p₁.

[math]\displaystyle{ \beta_0 = \frac{\mathbf{r}_1^\mathsf{T} \mathbf{r}_1}{\mathbf{r}_0^\mathsf{T} \mathbf{r}_0} \approx \frac{\begin{bmatrix} -0.2810 & 0.7492 \end{bmatrix} \begin{bmatrix} -0.2810 \\ 0.7492 \end{bmatrix}}{\begin{bmatrix} -8 & -3 \end{bmatrix} \begin{bmatrix} -8 \\ -3 \end{bmatrix}} = 0.0088. }[/math]

Now, using this scalar β₀, we can compute the next search direction p₁ using the relationship

[math]\displaystyle{ \mathbf{p}_1 = \mathbf{r}_1 + \beta_0 \mathbf{p}_0 \approx \begin{bmatrix} -0.2810 \\ 0.7492 \end{bmatrix} + 0.0088 \begin{bmatrix} -8 \\ -3 \end{bmatrix} = \begin{bmatrix} -0.3511 \\ 0.7229 \end{bmatrix}. }[/math]

We now compute the scalar α₁ using our newly acquired p₁ using the same method as that used for α₀.

[math]\displaystyle{ \alpha_1 = \frac{\mathbf{r}_1^\mathsf{T} \mathbf{r}_1}{\mathbf{p}_1^\mathsf{T} \mathbf{A p}_1} \approx \frac{\begin{bmatrix} -0.2810 & 0.7492 \end{bmatrix} \begin{bmatrix} -0.2810 \\ 0.7492 \end{bmatrix}}{ \begin{bmatrix} -0.3511 & 0.7229 \end{bmatrix} \begin{bmatrix} 4 & 1 \\ 1 & 3 \end{bmatrix} \begin{bmatrix} -0.3511 \\ 0.7229 \end{bmatrix} } = 0.4122. }[/math]

Finally, we find x₂ using the same method as that used to find x₁.

[math]\displaystyle{ \mathbf{x}_2 = \mathbf{x}_1 + \alpha_1 \mathbf{p}_1 \approx \begin{bmatrix} 0.2356 \\ 0.3384 \end{bmatrix} + 0.4122 \begin{bmatrix} -0.3511 \\ 0.7229 \end{bmatrix} = \begin{bmatrix} 0.0909 \\ 0.6364 \end{bmatrix}. }[/math]

The result, x₂, is a "better" approximation to the system's solution than x₁ and x₀. If exact arithmetic were to be used in this example instead of limited-precision, then the exact solution would theoretically have been reached after n = 2 iterations (n being the order of the system).

Convergence properties

The conjugate gradient method can theoretically be viewed as a direct method, as in the absence of round-off error it produces the exact solution after a finite number of iterations, which is not larger than the size of the matrix. In practice, the exact solution is never obtained since the conjugate gradient method is unstable with respect to even small perturbations, e.g., most directions are not in practice conjugate, due to a degenerative nature of generating the Krylov subspaces.

As an iterative method, the conjugate gradient method monotonically (in the energy norm) improves approximations [math]\displaystyle{ \mathbf{x}_{k} }[/math] to the exact solution and may reach the required tolerance after a relatively small (compared to the problem size) number of iterations. The improvement is typically linear and its speed is determined by the condition number [math]\displaystyle{ \kappa(A) }[/math] of the system matrix [math]\displaystyle{ A }[/math]: the larger [math]\displaystyle{ \kappa(A) }[/math] is, the slower the improvement.

If [math]\displaystyle{ \kappa(A) }[/math] is large, preconditioning is commonly used to replace the original system [math]\displaystyle{ \mathbf{A x}-\mathbf{b} = 0 }[/math] with [math]\displaystyle{ \mathbf{M}^{-1}(\mathbf{A x}-\mathbf{b}) = 0 }[/math] such that [math]\displaystyle{ \kappa(\mathbf{M}^{-1}\mathbf{A}) }[/math] is smaller than [math]\displaystyle{ \kappa(\mathbf{A}) }[/math], see below.

Convergence theorem

Define a subset of polynomials as

[math]\displaystyle{ \Pi_k^* := \left\lbrace \ p \in \Pi_k \ : \ p(0)=1 \ \right\rbrace \,, }[/math]

where [math]\displaystyle{ \Pi_k }[/math] is the set of polynomials of maximal degree [math]\displaystyle{ k }[/math].

Let [math]\displaystyle{ \left( \mathbf{x}_k \right)_k }[/math] be the iterative approximations of the exact solution [math]\displaystyle{ \mathbf{x}_* }[/math], and define the errors as [math]\displaystyle{ \mathbf{e}_k := \mathbf{x}_k - \mathbf{x}_* }[/math]. Now, the rate of convergence can be approximated as

[math]\displaystyle{ \begin{align} \left\| \mathbf{e}_k \right\|_\mathbf{A} &= \min_{p \in \Pi_k^*} \left\| p(\mathbf{A}) \mathbf{e}_0 \right\|_\mathbf{A} \\ &\leq \min_{p \in \Pi_k^*} \, \max_{ \lambda \in \sigma(\mathbf{A})} | p(\lambda) | \ \left\| \mathbf{e}_0 \right\|_\mathbf{A} \\ &\leq 2 \left( \frac{ \sqrt{\kappa(\mathbf{A})}-1 }{ \sqrt{\kappa(\mathbf{A})}+1 } \right)^k \ \left\| \mathbf{e}_0 \right\|_\mathbf{A} \\ &\leq 2 \exp\left(\frac{-2k}{\sqrt{\kappa(\mathbf{A})}}\right) \ \left\| \mathbf{e}_0 \right\|_\mathbf{A} \,, \end{align} }[/math]

where [math]\displaystyle{ \sigma(\mathbf{A}) }[/math] denotes the spectrum, and [math]\displaystyle{ \kappa(\mathbf{A}) }[/math] denotes the condition number.

This shows [math]\displaystyle{ k = \tfrac{1}{2}\sqrt{\kappa(\mathbf{A})} \log\left(\left\| \mathbf{e}_0 \right\|_\mathbf{A} \varepsilon^{-1}\right) }[/math] iterations suffices to reduce the error to [math]\displaystyle{ 2\varepsilon }[/math] for any [math]\displaystyle{ \varepsilon\gt 0 }[/math].

Note, the important limit when [math]\displaystyle{ \kappa(\mathbf{A}) }[/math] tends to [math]\displaystyle{ \infty }[/math]

[math]\displaystyle{ \frac{ \sqrt{\kappa(\mathbf{A})}-1 }{ \sqrt{\kappa(\mathbf{A})}+1 } \approx 1 - \frac{2}{\sqrt{\kappa(\mathbf{A})}} \quad \text{for} \quad \kappa(\mathbf{A}) \gg 1 \,. }[/math]

This limit shows a faster convergence rate compared to the iterative methods of Jacobi or Gauss–Seidel which scale as [math]\displaystyle{ \approx 1 - \frac{2}{\kappa(\mathbf{A})} }[/math].

No round-off error is assumed in the convergence theorem, but the convergence bound is commonly valid in practice as theoretically explained by Anne Greenbaum.

Practical convergence

If initialized randomly, the first stage of iterations is often the fastest, as the error is eliminated within the Krylov subspace that initially reflects a smaller effective condition number. The second stage of convergence is typically well defined by the theoretical convergence bound with [math]\displaystyle{ \sqrt{\kappa(\mathbf{A})} }[/math], but may be super-linear, depending on a distribution of the spectrum of the matrix [math]\displaystyle{ A }[/math] and the spectral distribution of the error. In the last stage, the smallest attainable accuracy is reached and the convergence stalls or the method may even start diverging. In typical scientific computing applications in double-precision floating-point format for matrices of large sizes, the conjugate gradient method uses a stopping criteria with a tolerance that terminates the iterations during the first or second stage.

The preconditioned conjugate gradient method

In most cases, preconditioning is necessary to ensure fast convergence of the conjugate gradient method. If [math]\displaystyle{ \mathbf{M}^{-1} }[/math] is symmetric positive-definite and [math]\displaystyle{ \mathbf{M}^{-1}\mathbf{A} }[/math] has a better condition number than [math]\displaystyle{ \mathbf{A} }[/math], a preconditioned conjugate gradient method can be used. It takes the following form:

[math]\displaystyle{ \mathbf{r}_0 := \mathbf{b} - \mathbf{A x}_0 }[/math]

[math]\displaystyle{ \textrm{Solve:}\mathbf{M}\mathbf{z}_0 := \mathbf{r}_0 }[/math]

[math]\displaystyle{ \mathbf{p}_0 := \mathbf{z}_0 }[/math]

[math]\displaystyle{ k := 0 \, }[/math]

repeat

[math]\displaystyle{ \alpha_k := \frac{\mathbf{r}_k^\mathsf{T} \mathbf{z}_k}{\mathbf{p}_k^\mathsf{T} \mathbf{A p}_k} }[/math]

[math]\displaystyle{ \mathbf{x}_{k+1} := \mathbf{x}_k + \alpha_k \mathbf{p}_k }[/math]

[math]\displaystyle{ \mathbf{r}_{k+1} := \mathbf{r}_k - \alpha_k \mathbf{A p}_k }[/math]

if r_k+1 is sufficiently small then exit loop end if

[math]\displaystyle{ \mathrm{Solve}\ \mathbf{M}\mathbf{z}_{k+1} := \mathbf{r}_{k+1} }[/math]

[math]\displaystyle{ \beta_k := \frac{\mathbf{r}_{k+1}^\mathsf{T} \mathbf{z}_{k+1}}{\mathbf{r}_k^\mathsf{T} \mathbf{z}_k} }[/math]

[math]\displaystyle{ \mathbf{p}_{k+1} := \mathbf{z}_{k+1} + \beta_k \mathbf{p}_k }[/math]

[math]\displaystyle{ k := k + 1 \, }[/math]

end repeat

The result is x_k+1

The above formulation is equivalent to applying the regular conjugate gradient method to the preconditioned system

[math]\displaystyle{ \mathbf{E}^{-1}\mathbf{A}(\mathbf{E}^{-1})^\mathsf{T}\mathbf{\hat{x}}=\mathbf{E}^{-1}\mathbf{b} }[/math]

where

[math]\displaystyle{ \mathbf{EE}^\mathsf{T}=\mathbf{M}, \qquad \mathbf{\hat{x}}=\mathbf{E}^\mathsf{T}\mathbf{x}. }[/math]

The Cholesky decomposition of the preconditioner must be used to keep the symmetry (and positive definiteness) of the system. However, this decomposition does not need to be computed, and it is sufficient to know [math]\displaystyle{ \mathbf{M}^{-1} }[/math]. It can be shown that [math]\displaystyle{ \mathbf{E}^{-1}\mathbf{A}(\mathbf{E}^{-1})^\mathsf{T} }[/math] has the same spectrum as [math]\displaystyle{ \mathbf{M}^{-1}\mathbf{A} }[/math].

The preconditioner matrix M has to be symmetric positive-definite and fixed, i.e., cannot change from iteration to iteration. If any of these assumptions on the preconditioner is violated, the behavior of the preconditioned conjugate gradient method may become unpredictable.

An example of a commonly used preconditioner is the incomplete Cholesky factorization.

Using the preconditioner in practice

It is importart to keep in mind that we don't want to invert the matrix [math]\displaystyle{ \mathbf{M} }[/math] explicitly in order to get [math]\displaystyle{ \mathbf{M}^{-1} }[/math] for use it in the process, since inverting [math]\displaystyle{ \mathbf{M} }[/math] would take more time/computational resources than solving the conjugate gradient algorithm itself. As an example, let's say that we are using a preconditioner coming from incomplete Cholesky factorization. The resulting matrix is the lower triangular matrix [math]\displaystyle{ \mathbf{L} }[/math], and the preconditioner matrix is:

[math]\displaystyle{ \mathbf{M}=\mathbf{LL}^\mathsf{T} }[/math]

Then we have to solve:

[math]\displaystyle{ \mathbf{Mz}=\mathbf{r} }[/math]

[math]\displaystyle{ \mathbf{z}=\mathbf{M}^{-1}\mathbf{r} }[/math]

But:

[math]\displaystyle{ \mathbf{M}^{-1}=(\mathbf{L}^{-1})^\mathsf{T}\mathbf{L}^{-1} }[/math]

Then:

[math]\displaystyle{ \mathbf{z}=(\mathbf{L}^{-1})^\mathsf{T}\mathbf{L}^{-1}\mathbf{r} }[/math]

Let's take an intermediary vector [math]\displaystyle{ \mathbf{a} }[/math]:

[math]\displaystyle{ \mathbf{a}=\mathbf{L}^{-1}\mathbf{r} }[/math]

[math]\displaystyle{ \mathbf{r}=\mathbf{L}\mathbf{a} }[/math]

Since [math]\displaystyle{ \mathbf{r} }[/math] and [math]\displaystyle{ \mathbf{L} }[/math] and known, and [math]\displaystyle{ \mathbf{L} }[/math] is lower triangular, solving for [math]\displaystyle{ \mathbf{a} }[/math] is easy and computationally cheap by using forward substitution. Then, we substitute [math]\displaystyle{ \mathbf{a} }[/math] in the original equation:

[math]\displaystyle{ \mathbf{z}=(\mathbf{L}^{-1})^\mathsf{T}\mathbf{a} }[/math]

[math]\displaystyle{ \mathbf{a}=\mathbf{L}^\mathsf{T}\mathbf{z} }[/math]

Since [math]\displaystyle{ \mathbf{a} }[/math] and [math]\displaystyle{ \mathbf{L}^\mathsf{T} }[/math] are known, and [math]\displaystyle{ \mathbf{L}^\mathsf{T} }[/math] is upper triangular, solving for [math]\displaystyle{ \mathbf{z} }[/math] is easy and computationally cheap by using backward substitution.

Using this method, there is no need to invert [math]\displaystyle{ \mathbf{M} }[/math] or [math]\displaystyle{ \mathbf{L} }[/math] explicitly at all, and we still obtain [math]\displaystyle{ \mathbf{z} }[/math].

The flexible preconditioned conjugate gradient method

In numerically challenging applications, sophisticated preconditioners are used, which may lead to variable preconditioning, changing between iterations. Even if the preconditioner is symmetric positive-definite on every iteration, the fact that it may change makes the arguments above invalid, and in practical tests leads to a significant slow down of the convergence of the algorithm presented above. Using the Polak–Ribière formula

[math]\displaystyle{ \beta_k := \frac{\mathbf{r}_{k+1}^\mathsf{T} \left(\mathbf{z}_{k+1}-\mathbf{z}_{k}\right)}{\mathbf{r}_k^\mathsf{T} \mathbf{z}_k} }[/math]

instead of the Fletcher–Reeves formula

[math]\displaystyle{ \beta_k := \frac{\mathbf{r}_{k+1}^\mathsf{T} \mathbf{z}_{k+1}}{\mathbf{r}_k^\mathsf{T} \mathbf{z}_k} }[/math]

may dramatically improve the convergence in this case. This version of the preconditioned conjugate gradient method can be called flexible, as it allows for variable preconditioning. The flexible version is also shown to be robust even if the preconditioner is not symmetric positive definite (SPD).

The implementation of the flexible version requires storing an extra vector. For a fixed SPD preconditioner, [math]\displaystyle{ \mathbf{r}_{k+1}^\mathsf{T} \mathbf{z}_{k}=0, }[/math] so both formulas for β_k are equivalent in exact arithmetic, i.e., without the round-off error.

The mathematical explanation of the better convergence behavior of the method with the Polak–Ribière formula is that the method is locally optimal in this case, in particular, it does not converge slower than the locally optimal steepest descent method.

Vs. the locally optimal steepest descent method

In both the original and the preconditioned conjugate gradient methods one only needs to set [math]\displaystyle{ \beta_k := 0 }[/math] in order to make them locally optimal, using the line search, steepest descent methods. With this substitution, vectors p are always the same as vectors z, so there is no need to store vectors p. Thus, every iteration of these steepest descent methods is a bit cheaper compared to that for the conjugate gradient methods. However, the latter converge faster, unless a (highly) variable and/or non-SPD preconditioner is used, see above.

Conjugate gradient method as optimal feedback controller for double integrator

The conjugate gradient method can also be derived using optimal control theory. In this approach, the conjugate gradient method falls out as an optimal feedback controller,[math]\displaystyle{ u = k(x, v):= -\gamma_a \nabla f(x) - \gamma_b v }[/math] for the double integrator system,[math]\displaystyle{ \dot x = v, \quad \dot v = u }[/math] The quantities [math]\displaystyle{ \gamma_a }[/math] and [math]\displaystyle{ \gamma_b }[/math] are variable feedback gains.

Conjugate gradient on the normal equations

The conjugate gradient method can be applied to an arbitrary n-by-m matrix by applying it to normal equations A^TA and right-hand side vector A^Tb, since A^TA is a symmetric positive-semidefinite matrix for any A. The result is conjugate gradient on the normal equations (CGN or CGNR).

A^TAx = A^Tb

As an iterative method, it is not necessary to form A^TA explicitly in memory but only to perform the matrix–vector and transpose matrix–vector multiplications. Therefore, CGNR is particularly useful when A is a sparse matrix since these operations are usually extremely efficient. However the downside of forming the normal equations is that the condition number κ(A^TA) is equal to κ²(A) and so the rate of convergence of CGNR may be slow and the quality of the approximate solution may be sensitive to roundoff errors. Finding a good preconditioner is often an important part of using the CGNR method.

Several algorithms have been proposed (e.g., CGLS, LSQR). The LSQR algorithm purportedly has the best numerical stability when A is ill-conditioned, i.e., A has a large condition number.

Conjugate gradient method for complex Hermitian matrices

The conjugate gradient method with a trivial modification is extendable to solving, given complex-valued matrix A and vector b, the system of linear equations [math]\displaystyle{ \mathbf {A} \mathbf {x} =\mathbf {b} }[/math] for the complex-valued vector x, where A is Hermitian (i.e., A' = A) and positive-definite matrix, and the symbol ' denotes the conjugate transpose. The trivial modification is simply substituting the conjugate transpose for the real transpose everywhere.

Advantages and disadvantages

The advantages and disadvantages of the conjugate gradient methods are summarized in the lecture notes by Nemirovsky and BenTal.

A pathological example

This example is from Let [math]\displaystyle{ t \in (0, 1) }[/math], and define[math]\displaystyle{ W= \begin{bmatrix} t & \sqrt{t} & & & & \\ \sqrt{t} & 1+t & \sqrt{t} & & & \\ & \sqrt{t} & 1+t & \sqrt{t} & & \\ & & \sqrt{t} & \ddots & \ddots & \\ & & & \ddots & & \\ & & & & & \sqrt{t} \\ & & & & \sqrt{t} & 1+t \end{bmatrix}, \quad b=\begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix} }[/math]Since [math]\displaystyle{ W }[/math] is invertible, there exists a unique solution to [math]\displaystyle{ W x = b }[/math]. Solving it by conjugate gradient descent gives us rather bad convergence:[math]\displaystyle{ \|b- Wx_k\|^2 = (1/t)^{k}, \quad \|b- Wx_n\|^2 =0 }[/math]In words, during the CG process, the error grows exponentially, until it suddenly becomes zero as the unique solution is found.

See also

• Biconjugate gradient method (BiCG)
• Conjugate gradient squared method (CGS)
• Conjugate residual method
• Gaussian belief propagation
• Iterative method: Linear systems
• Krylov subspace
• Nonlinear conjugate gradient method
• Preconditioning
• Sparse matrix–vector multiplication

Further reading

• Atkinson, Kendell A. (1988). "Section 8.9". An introduction to numerical analysis (2nd ed.). John Wiley and Sons. ISBN 978-0-471-50023-0. https://archive.org/details/introductiontonu0000atki. 
• Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 978-0-486-43227-4. 
• Golub, Gene H.; Van Loan, Charles F. (2013). "Chapter 11". Matrix Computations (4th ed.). Johns Hopkins University Press. ISBN 978-1-4214-0794-4. 
• Saad, Yousef (2003-04-01). "Chapter 6". Iterative methods for sparse linear systems (2nd ed.). SIAM. ISBN 978-0-89871-534-7. https://archive.org/details/iterativemethods0000saad. 
• Gérard Meurant: "Detection and correction of silent errors in the conjugate gradient algorithm", Numerical Algorithms, vol.92 (2023), pp.869-891. url=https://doi.org/10.1007/s11075-022-01380-1

External links

• Hazewinkel, Michiel, ed. (2001), "Conjugate gradients, method of", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/c025030