Automata theory

Short description: Study of abstract machines and automata

Classes of automata

The automaton described by this state diagram starts in state S₁, and changes states following the arrows marked 0 or 1 according to the input symbols as they arrive. The double circle marks S₁ as an accepting state. Since all paths from S₁ to itself contain an even number of arrows marked 0, this automaton accepts strings containing even numbers of 0s.

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to mathematical logic. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton (automata in plural) is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a Finite Automaton (FA) or Finite-State Machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states (represented in the figure by circles) and transitions (represented by arrows). As the automaton sees a symbol of input, it makes a transition (or jump) to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.

Automata theory is closely related to formal language theory. In this context, automata are used as finite representations of formal languages that may be infinite. Automata are often classified by the class of formal languages they can recognize, as in the Chomsky hierarchy, which describes a nesting relationship between major classes of automata. Automata play a major role in the theory of computation, compiler construction, artificial intelligence, parsing and formal verification.

History

The theory of abstract automata was developed in the mid-20th century in connection with finite automata. Automata theory was initially considered a branch of mathematical systems theory, studying the behavior of discrete-parameter systems. Early work in automata theory differed from previous work on systems by using abstract algebra to describe information systems rather than differential calculus to describe material systems. The theory of the finite-state transducer was developed under different names by different research communities. The earlier concept of Turing machine was also included in the discipline along with new forms of infinite-state automata, such as pushdown automata.

1956 saw the publication of Automata Studies, which collected work by scientists including Claude Shannon, W. Ross Ashby, John von Neumann, Marvin Minsky, Edward F. Moore, and Stephen Cole Kleene. With the publication of this volume, "automata theory emerged as a relatively autonomous discipline". The book included Kleene's description of the set of regular events, or regular languages, and a relatively stable measure of complexity in Turing machine programs by Shannon. In the same year, Noam Chomsky described the Chomsky hierarchy, a correspondence between automata and formal grammars, and Ross Ashby published An Introduction to Cybernetics, an accessible textbook explaining automata and information using basic set theory.

The study of linear bounded automata led to the Myhill–Nerode theorem, which gives a necessary and sufficient condition for a formal language to be regular, and an exact count of the number of states in a minimal machine for the language. The pumping lemma for regular languages, also useful in regularity proofs, was proven in this period by Michael O. Rabin and Dana Scott, along with the computational equivalence of deterministic and nondeterministic finite automata.

In the 1960s, a body of algebraic results known as "structure theory" or "algebraic decomposition theory" emerged, which dealt with the realization of sequential machines from smaller machines by interconnection. While any finite automaton can be simulated using a universal gate set, this requires that the simulating circuit contain loops of arbitrary complexity. Structure theory deals with the "loop-free" realizability of machines. The theory of computational complexity also took shape in the 1960s. By the end of the decade, automata theory came to be seen as "the pure mathematics of computer science".

Automata

What follows is a general definition of an automaton, which restricts a broader definition of a system to one viewed as acting in discrete time-steps, with its state behavior and outputs defined at each step by unchanging functions of only its state and input.

Informal description

An automaton runs when it is given some sequence of inputs in discrete (individual) time steps (or just steps). An automaton processes one input picked from a set of symbols or letters, which is called an input alphabet. The symbols received by the automaton as input at any step are a sequence of symbols called words. An automaton has a set of states. At each moment during a run of the automaton, the automaton is in one of its states. When the automaton receives new input, it moves to another state (or transitions) based on a transition function that takes the previous state and current input symbol as parameters. At the same time, another function called the output function produces symbols from the output alphabet, also according to the previous state and current input symbol. The automaton reads the symbols of the input word and transitions between states until the word is read completely, if it is finite in length, at which point the automaton halts. A state at which the automaton halts is called the final state.

To investigate the possible state/input/output sequences in an automaton using formal language theory, a machine can be assigned a starting state and a set of accepting states. Then, depending on whether a run starting from the starting state ends in an accepting state, the automaton can be said to accept or reject an input sequence. The set of all the words accepted by an automaton is called the language recognized by the automaton. A familiar example of a machine recognizing a language is an electronic lock, which accepts or rejects attempts to enter the correct code.

Formal definition

Automaton

An automaton can be represented formally by a quintuple [math]\displaystyle{ M = \langle \Sigma, \Gamma, Q, \delta, \lambda \rangle }[/math], where:

• [math]\displaystyle{ \Sigma }[/math] is a finite set of symbols, called the input alphabet of the automaton,
• [math]\displaystyle{ \Gamma }[/math] is another finite set of symbols, called the output alphabet of the automaton,
• [math]\displaystyle{ Q }[/math] is a set of states,
• [math]\displaystyle{ \delta }[/math] is the next-state function or transition function [math]\displaystyle{ \delta : Q \times \Sigma \to Q }[/math] mapping state-input pairs to successor states,
• [math]\displaystyle{ \lambda }[/math] is the next-output function [math]\displaystyle{ \lambda : Q \times \Sigma \to \Gamma }[/math] mapping state-input pairs to outputs.

If [math]\displaystyle{ Q }[/math] is finite, then [math]\displaystyle{ M }[/math] is a finite automaton.

Input word

An automaton reads a finite string of symbols [math]\displaystyle{ a_1a_2...a_n }[/math], where [math]\displaystyle{ a_i \in \Sigma }[/math], which is called an input word. The set of all words is denoted by [math]\displaystyle{ \Sigma^* }[/math].

Run

A sequence of states [math]\displaystyle{ q_0,q_1,...,q_n }[/math], where [math]\displaystyle{ q_i \in Q }[/math] such that [math]\displaystyle{ q_i = \delta(q_{i-1}, a_i) }[/math] for [math]\displaystyle{ 0 \lt i \le n }[/math], is a run of the automaton on an input [math]\displaystyle{ a_1a_2...a_n \in \Sigma^* }[/math] starting from state [math]\displaystyle{ q_0 }[/math]. In other words, at first the automaton is at the start state [math]\displaystyle{ q_0 }[/math], and receives input [math]\displaystyle{ a_1 }[/math]. For [math]\displaystyle{ a_1 }[/math] and every following [math]\displaystyle{ a_i }[/math] in the input string, the automaton picks the next state [math]\displaystyle{ q_i }[/math] according to the transition function [math]\displaystyle{ \delta(q_{i-1},a_i) }[/math], until the last symbol [math]\displaystyle{ a_n }[/math] has been read, leaving the machine in the final state of the run, [math]\displaystyle{ q_n }[/math]. Similarly, at each step, the automaton emits an output symbol according to the output function [math]\displaystyle{ \lambda(q_{i-1},a_i) }[/math].

The transition function [math]\displaystyle{ \delta }[/math] is extended inductively into [math]\displaystyle{ \overline\delta: Q \times \Sigma^* \to Q }[/math] to describe the machine's behavior when fed whole input words. For the empty string [math]\displaystyle{ \varepsilon }[/math], [math]\displaystyle{ \overline\delta(q, \varepsilon) = q }[/math] for all states [math]\displaystyle{ q }[/math], and for strings [math]\displaystyle{ wa }[/math] where [math]\displaystyle{ a }[/math] is the last symbol and [math]\displaystyle{ w }[/math] is the (possibly empty) rest of the string, [math]\displaystyle{ \overline\delta(q, wa) = \delta(\overline\delta(q,w),a) }[/math]. The output function [math]\displaystyle{ \lambda }[/math] may be extended similarly into [math]\displaystyle{ \overline\lambda(q,w) }[/math], which gives the complete output of the machine when run on word [math]\displaystyle{ w }[/math] from state [math]\displaystyle{ q }[/math].

Acceptor

In order to study an automaton with the theory of formal languages, an automaton may be considered as an acceptor, replacing the output alphabet and function [math]\displaystyle{ \Gamma }[/math] and [math]\displaystyle{ \lambda }[/math] with

• [math]\displaystyle{ q_0 \in Q }[/math], a designated start state, and
• [math]\displaystyle{ F }[/math], a set of states of [math]\displaystyle{ Q }[/math] (i.e. [math]\displaystyle{ F \subseteq Q }[/math]) called accept states.

This allows the following to be defined:

Accepting word

A word [math]\displaystyle{ w = a_1a_2...a_n \in \Sigma^* }[/math] is an accepting word for the automaton if [math]\displaystyle{ \overline\delta(q_0,w) \in F }[/math], that is, if after consuming the whole string [math]\displaystyle{ w }[/math] the machine is in an accept state.

Recognized language

The language [math]\displaystyle{ L \subseteq \Sigma^* }[/math] recognized by an automaton is the set of all the words that are accepted by the automaton, [math]\displaystyle{ L = \{w \in \Sigma^* \ |\ \overline\delta(q_0,w) \in F\} }[/math].

Recognizable languages

The recognizable languages are the set of languages that are recognized by some automaton. For finite automata the recognizable languages are regular languages. For different types of automata, the recognizable languages are different.

Variant definitions of automata

Automata are defined to study useful machines under mathematical formalism. So the definition of an automaton is open to variations according to the "real world machine" that we want to model using the automaton. People have studied many variations of automata. The following are some popular variations in the definition of different components of automata.

Input

• Finite input: An automaton that accepts only finite sequences of symbols. The above introductory definition only encompasses finite words.
• Infinite input: An automaton that accepts infinite words (ω-words). Such automata are called ω-automata.
• Tree input: The input may be a tree of symbols instead of sequence of symbols. In this case after reading each symbol, the automaton reads all the successor symbols in the input tree. It is said that the automaton makes one copy of itself for each successor and each such copy starts running on one of the successor symbols from the state according to the transition relation of the automaton. Such an automaton is called a tree automaton.
• Infinite tree input : The two extensions above can be combined, so the automaton reads a tree structure with (in)finite branches. Such an automaton is called an infinite tree automaton.

States

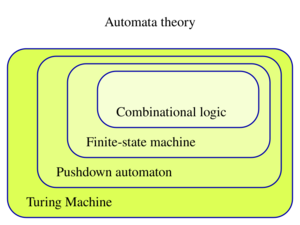
• Single state: An automaton with one state, also called a combinational circuit, performs a transformation which may implement combinational logic.
• Finite states: An automaton that contains only a finite number of states.
• Infinite states: An automaton that may not have a finite number of states, or even a countable number of states. Different kinds of abstract memory may be used to give such machines finite descriptions.
• Stack memory: An automaton may also contain some extra memory in the form of a stack in which symbols can be pushed and popped. This kind of automaton is called a pushdown automaton.
• Queue memory: An automaton may have memory in the form of a queue. Such a machine is called queue machine and is Turing-complete.
• Tape memory: The inputs and outputs of automata are often described as input and output tapes. Some machines have additional working tapes, including the Turing machine, linear bounded automaton, and log-space transducer.

Transition function

• Deterministic: For a given current state and an input symbol, if an automaton can only jump to one and only one state then it is a deterministic automaton.
• Nondeterministic: An automaton that, after reading an input symbol, may jump into any of a number of states, as licensed by its transition relation. The term transition function is replaced by transition relation: The automaton non-deterministically decides to jump into one of the allowed choices. Such automata are called nondeterministic automata.
• Alternation: This idea is quite similar to tree automata but orthogonal. The automaton may run its multiple copies on the same next read symbol. Such automata are called alternating automata. The acceptance condition must be satisfied on all runs of such copies to accept the input.
• Two-wayness: Automata may read their input from left to right, or they may be allowed to move back-and-forth on the input, in a way similar to a Turing machine. Automata which can move back-and-forth on the input are called two-way finite automata.

Acceptance condition

• Acceptance of finite words: Same as described in the informal definition above.
• Acceptance of infinite words: an ω-automaton cannot have final states, as infinite words never terminate. Rather, acceptance of the word is decided by looking at the infinite sequence of visited states during the run.
• Probabilistic acceptance: An automaton need not strictly accept or reject an input. It may accept the input with some probability between zero and one. For example, quantum finite automata, geometric automata and metric automata have probabilistic acceptance.

Different combinations of the above variations produce many classes of automata.

Automata theory is a subject matter that studies properties of various types of automata. For example, the following questions are studied about a given type of automata.

• Which class of formal languages is recognizable by some type of automata? (Recognizable languages)
• Are certain automata closed under union, intersection, or complementation of formal languages? (Closure properties)
• How expressive is a type of automata in terms of recognizing a class of formal languages? And, their relative expressive power? (Language hierarchy)

Automata theory also studies the existence or nonexistence of any effective algorithms to solve problems similar to the following list:

• Does an automaton accept at least one input word? (Emptiness checking)
• Is it possible to transform a given non-deterministic automaton into a deterministic automaton without changing the language recognized? (Determinization)
• For a given formal language, what is the smallest automaton that recognizes it? (Minimization)

Types of automata

The following is an incomplete list of types of automata.

Automaton	Recognizable languages
Nondeterministic/Deterministic finite-state machine (FSM)	regular languages
Deterministic pushdown automaton (DPDA)	deterministic context-free languages
Pushdown automaton (PDA)	context-free languages
Linear bounded automaton (LBA)	context-sensitive languages
Turing machine	recursively enumerable languages
Deterministic Büchi automaton	ω-limit languages
Nondeterministic Büchi automaton	ω-regular languages
Rabin automaton, Streett automaton, Parity automaton, Muller automaton
Weighted automaton

Discrete, continuous, and hybrid automata

Normally automata theory describes the states of abstract machines but there are discrete automata, analog automata or continuous automata, or hybrid discrete-continuous automata, which use digital data, analog data or continuous time, or digital and analog data, respectively.

Hierarchy in terms of powers

The following is an incomplete hierarchy in terms of powers of different types of virtual machines. The hierarchy reflects the nested categories of languages the machines are able to accept.

Automaton

Deterministic Finite Automaton (DFA) -- Lowest Power (same power)    [math]\displaystyle{ || }[/math]   (same power) Nondeterministic Finite Automaton (NFA) (above is weaker)    [math]\displaystyle{ \cap }[/math]    (below is stronger) Deterministic Push Down Automaton (DPDA-I) with 1 push-down store [math]\displaystyle{ \cap }[/math] Nondeterministic Push Down Automaton (NPDA-I) with 1 push-down store [math]\displaystyle{ \cap }[/math] Linear Bounded Automaton (LBA) [math]\displaystyle{ \cap }[/math] Deterministic Push Down Automaton (DPDA-II) with 2 push-down stores [math]\displaystyle{ || }[/math] Nondeterministic Push Down Automaton (NPDA-II) with 2 push-down stores [math]\displaystyle{ || }[/math] Deterministic Turing Machine (DTM) [math]\displaystyle{ || }[/math] Nondeterministic Turing Machine (NTM) [math]\displaystyle{ || }[/math] Probabilistic Turing Machine (PTM) [math]\displaystyle{ || }[/math] Multitape Turing Machine (MTM) [math]\displaystyle{ || }[/math] Multidimensional Turing Machine

Applications

Each model in automata theory plays important roles in several applied areas. Finite automata are used in text processing, compilers, and hardware design. Context-free grammar (CFGs) are used in programming languages and artificial intelligence. Originally, CFGs were used in the study of human languages. Cellular automata are used in the field of artificial life, the most famous example being John Conway's Game of Life. Some other examples which could be explained using automata theory in biology include mollusk and pine cone growth and pigmentation patterns. Going further, a theory suggesting that the whole universe is computed by some sort of a discrete automaton, is advocated by some scientists. The idea originated in the work of Konrad Zuse, and was popularized in America by Edward Fredkin. Automata also appear in the theory of finite fields: the set of irreducible polynomials that can be written as composition of degree two polynomials is in fact a regular language. Another problem for which automata can be used is the induction of regular languages.

Automata simulators

Automata simulators are pedagogical tools used to teach, learn and research automata theory. An automata simulator takes as input the description of an automaton and then simulates its working for an arbitrary input string. The description of the automaton can be entered in several ways. An automaton can be defined in a symbolic language or its specification may be entered in a predesigned form or its transition diagram may be drawn by clicking and dragging the mouse. Well known automata simulators include Turing's World, JFLAP, VAS, TAGS and SimStudio.

Connection to category theory

One can define several distinct categories of automata following the automata classification into different types described in the previous section. The mathematical category of deterministic automata, sequential machines or sequential automata, and Turing machines with automata homomorphisms defining the arrows between automata is a Cartesian closed category, it has both categorical limits and colimits. An automata homomorphism maps a quintuple of an automaton A_i onto the quintuple of another automaton A_j. Automata homomorphisms can also be considered as automata transformations or as semigroup homomorphisms, when the state space, S, of the automaton is defined as a semigroup S_g. Monoids are also considered as a suitable setting for automata in monoidal categories.

Categories of variable automata

One could also define a variable automaton, in the sense of Norbert Wiener in his book on The Human Use of Human Beings via the endomorphisms [math]\displaystyle{ A_{i}\to A_{i} }[/math]. Then one can show that such variable automata homomorphisms form a mathematical group. In the case of non-deterministic, or other complex kinds of automata, the latter set of endomorphisms may become, however, a variable automaton groupoid. Therefore, in the most general case, categories of variable automata of any kind are categories of groupoids or groupoid categories. Moreover, the category of reversible automata is then a 2-category, and also a subcategory of the 2-category of groupoids, or the groupoid category.

See also

• Boolean differential calculus

Further reading

• John E. Hopcroft; Rajeev Motwani; Jeffrey D. Ullman (2000). Introduction to Automata Theory, Languages, and Computation (2nd ed.). Pearson Education. ISBN 978-0-201-44124-6. 
• Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 978-0-534-94728-6.  Part One: Automata and Languages, chapters 1–2, pp. 29–122. Section 4.1: Decidable Languages, pp. 152–159. Section 5.1: Undecidable Problems from Language Theory, pp. 172–183.
• Elaine Rich (2008). Automata, Computability and Complexity: Theory and Applications. Pearson. ISBN 978-0-13-228806-4. 
• Salomaa, Arto (1985). Computation and automata. Encyclopedia of Mathematics and Its Applications. 25. Cambridge University Press. ISBN 978-0-521-30245-6. https://archive.org/details/computationautom0000salo. 
• Anderson, James A. (2006). Automata theory with modern applications. With contributions by Tom Head. Cambridge: Cambridge University Press. ISBN 978-0-521-61324-8. 
• Conway, J.H. (1971). Regular algebra and finite machines. Chapman and Hall Mathematics Series. London: Chapman & Hall. 
• John M. Howie (1991) Automata and Languages, Clarendon Press ISBN:0-19-853424-8 MR1254435
• Sakarovitch, Jacques (2009). Elements of automata theory. Translated from the French by Reuben Thomas. Cambridge University Press. ISBN 978-0-521-84425-3. 
• James P. Schmeiser; David T. Barnard (1995). Producing a top-down parse order with bottom-up parsing. Elsevier North-Holland. 
• Igor Aleksander; F. Keith Hanna (1975). Automata Theory: An Engineering Approach. New York: Crane Russak. ISBN 978-0-8448-0657-0. 
• Marvin Minsky (1967). Computation: Finite and infinite machines. Princeton, N.J.: Prentice Hall. https://archive.org/details/computationfinit0000mins. 
• John C. Martin (2011). Introduction to Languages and The Theory of Computation. New York: McGraw Hill. ISBN 978-0-07-319146-1. 

External links

• dk.brics.automaton
• libfa