Cramér–Rao bound
In estimation theory and statistics, the Cramér–Rao bound (CRB) relates to estimation of a deterministic (fixed, though unknown) parameter. The result is named in honor of Harald Cramér and C. R. Rao,[1][2][3] but has also been derived independently by Maurice Fréchet,[4] Georges Darmois,[5] and by Alexander Aitken and Harold Silverstone.[6][7] It states that the precision of any unbiased estimator is at most the Fisher information; or (equivalently) the reciprocal of the Fisher information is a lower bound on its variance.
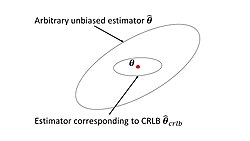
An unbiased estimator that achieves this bound is said to be (fully) efficient. Such a solution achieves the lowest possible mean squared error among all unbiased methods, and is therefore the minimum variance unbiased (MVU) estimator. However, in some cases, no unbiased technique exists which achieves the bound. This may occur either if for any unbiased estimator, there exists another with a strictly smaller variance, or if an MVU estimator exists, but its variance is strictly greater than the inverse of the Fisher information.
The Cramér–Rao bound can also be used to bound the variance of biased estimators of given bias. In some cases, a biased approach can result in both a variance and a mean squared error that are below the unbiased Cramér–Rao lower bound; see estimator bias.
Statement
The Cramér–Rao bound is stated in this section for several increasingly general cases, beginning with the case in which the parameter is a scalar and its estimator is unbiased. All versions of the bound require certain regularity conditions, which hold for most well-behaved distributions. These conditions are listed later in this section.
Scalar unbiased case
Suppose is an unknown deterministic parameter that is to be estimated from independent observations (measurements) of , each from a distribution according to some probability density function . The variance of any unbiased estimator of is then bounded[8] by the reciprocal of the Fisher information :
where the Fisher information is defined by
and is the natural logarithm of the likelihood function for a single sample and denotes the expected value with respect to the density of . If not indicated, in what follows, the expectation is taken with respect to .
If is twice differentiable and certain regularity conditions hold, then the Fisher information can also be defined as follows:[9]
The efficiency of an unbiased estimator measures how close this estimator's variance comes to this lower bound; estimator efficiency is defined as
or the minimum possible variance for an unbiased estimator divided by its actual variance. The Cramér–Rao lower bound thus gives
- .
General scalar case
A more general form of the bound can be obtained by considering a biased estimator , whose expectation is not but a function of this parameter, say, . Hence is not generally equal to 0. In this case, the bound is given by
where is the derivative of (by ), and is the Fisher information defined above.
Bound on the variance of biased estimators
Apart from being a bound on estimators of functions of the parameter, this approach can be used to derive a bound on the variance of biased estimators with a given bias, as follows.[10] Consider an estimator with bias , and let . By the result above, any unbiased estimator whose expectation is has variance greater than or equal to . Thus, any estimator whose bias is given by a function satisfies[11]
The unbiased version of the bound is a special case of this result, with .
It's trivial to have a small variance − an "estimator" that is constant has a variance of zero. But from the above equation we find that the mean squared error of a biased estimator is bounded by
using the standard decomposition of the MSE. Note, however, that if this bound might be less than the unbiased Cramér–Rao bound . For instance, in the example of estimating variance below, .
Multivariate case
Extending the Cramér–Rao bound to multiple parameters, define a parameter column vector
with probability density function which satisfies the two regularity conditions below.
The Fisher information matrix is a matrix with element defined as
Let be an estimator of any vector function of parameters, , and denote its expectation vector by . The Cramér–Rao bound then states that the covariance matrix of satisfies
- ,
where
- The matrix inequality is understood to mean that the matrix is positive semidefinite, and
- is the Jacobian matrix whose element is given by .
If is an unbiased estimator of (i.e., ), then the Cramér–Rao bound reduces to
If it is inconvenient to compute the inverse of the Fisher information matrix, then one can simply take the reciprocal of the corresponding diagonal element to find a (possibly loose) lower bound.[12]
Regularity conditions
The bound relies on two weak regularity conditions on the probability density function, , and the estimator :
- The Fisher information is always defined; equivalently, for all such that , exists, and is finite.
- The operations of integration with respect to and differentiation with respect to can be interchanged in the expectation of ; that is, whenever the right-hand side is finite. This condition can often be confirmed by using the fact that integration and differentiation can be swapped when either of the following cases hold:
- The function has bounded support in , and the bounds do not depend on ;
- The function has infinite support, is continuously differentiable, and the integral converges uniformly for all .
Proof
Proof for the general case based on the Chapman–Robbins bound
Proof based on.[13]
First equation:
Let be an infinitesimal, then for any , plugging in, we have
Plugging this into multivariate Chapman–Robbins bound gives .
Second equation:
It suffices to prove this for scalar case, with taking values in . Because for general , we can take any , then defining , the scalar case gives This holds for all , so we can concludeThe scalar case states that with .
Let be an infinitesimal, then for any , taking in the single-variate Chapman–Robbins bound gives .
By linear algebra, for any positive-definite matrix , thus we obtain
A standalone proof for the general scalar case
For the general scalar case:
Assume that is an estimator with expectation (based on the observations ), i.e. that . The goal is to prove that, for all ,
Let be a random variable with probability density function . Here is a statistic, which is used as an estimator for . Define as the score:
where the chain rule is used in the final equality above. Then the expectation of , written , is zero. This is because:
where the integral and partial derivative have been interchanged (justified by the second regularity condition).
If we consider the covariance of and , we have , because . Expanding this expression we have
again because the integration and differentiation operations commute (second condition).
The Cauchy–Schwarz inequality shows that
therefore
which proves the proposition.
Examples
Multivariate normal distribution
For the case of a d-variate normal distribution
the Fisher information matrix has elements[14]
where "tr" is the trace.
For example, let be a sample of independent observations with unknown mean and known variance .
Then the Fisher information is a scalar given by
and so the Cramér–Rao bound is
Normal variance with known mean
Suppose X is a normally distributed random variable with known mean and unknown variance . Consider the following statistic:
Then T is unbiased for , as . What is the variance of T?
(the second equality follows directly from the definition of variance). The first term is the fourth moment about the mean and has value ; the second is the square of the variance, or . Thus
Now, what is the Fisher information in the sample? Recall that the score is defined as
where is the likelihood function. Thus in this case,
where the second equality is from elementary calculus. Thus, the information in a single observation is just minus the expectation of the derivative of , or
Thus the information in a sample of independent observations is just times this, or
The Cramér–Rao bound states that
In this case, the inequality is saturated (equality is achieved), showing that the estimator is efficient.
However, we can achieve a lower mean squared error using a biased estimator. The estimator
obviously has a smaller variance, which is in fact
Its bias is
so its mean squared error is
which is clearly less than what unbiased estimators can achieve according to the Cramér–Rao bound.
When the mean is not known, the minimum mean squared error estimate of the variance of a sample from Gaussian distribution is achieved by dividing by , rather than or .
See also
References and notes
- ↑ Cramér, Harald (1946). Mathematical Methods of Statistics. Princeton, NJ: Princeton Univ. Press. ISBN 0-691-08004-6. OCLC 185436716. https://archive.org/details/in.ernet.dli.2015.223699.
- ↑ Rao, Calyampudi Radakrishna (1945). "Information and the accuracy attainable in the estimation of statistical parameters". Bulletin of the Calcutta Mathematical Society (Calcutta Mathematical Society) 37: 81–89.
- ↑ Rao, Calyampudi Radakrishna (1994). S. Das Gupta. ed. Selected Papers of C. R. Rao. New York: Wiley. ISBN 978-0-470-22091-7. OCLC 174244259.
- ↑ Fréchet, Maurice (1943). "Sur l'extension de certaines évaluations statistiques au cas de petits échantillons". Rev. Inst. Int. Statist. 11 (3/4): 182–205. doi:10.2307/1401114.
- ↑ Darmois, Georges (1945). "Sur les limites de la dispersion de certaines estimations". Rev. Int. Inst. Statist. 13 (1/4): 9–15. doi:10.2307/1400974.
- ↑ Aitken, A. C.; Silverstone, H. (1942). "XV.—On the Estimation of Statistical Parameters" (in en). Proceedings of the Royal Society of Edinburgh Section A: Mathematics 61 (2): 186–194. doi:10.1017/S008045410000618X. ISSN 2053-5902. https://www.cambridge.org/core/journals/proceedings-of-the-royal-society-of-edinburgh-section-a-mathematics/article/abs/xvon-the-estimation-of-statistical-parameters/74C2B968275EED1A954DB316FBC3635E.
- ↑ Shenton, L. R. (1970). "The so-called Cramer–Rao inequality". The American Statistician 24 (2): 36.
- ↑ Nielsen, Frank (2013). "Cramér-Rao Lower Bound and Information Geometry". Connected at Infinity II. Texts and Readings in Mathematics. 67. Hindustan Book Agency, Gurgaon. p. 18-37. doi:10.1007/978-93-86279-56-9_2. ISBN 978-93-80250-51-9.
- ↑ Suba Rao. "Lectures on statistical inference". http://www.stat.tamu.edu/~suhasini/teaching613/inference.pdf.
- ↑ "Cramér Rao Lower Bound - Navipedia". https://gssc.esa.int/navipedia/index.php/Cram%C3%A9r_Rao_Lower_Bound.
- ↑ "Cramér-Rao Bound". https://theoryandpractice.org/stats-ds-book/statistics/cramer-rao-bound.html.
- ↑ For the Bayesian case, see eqn. (11) of Bobrovsky; Mayer-Wolf; Zakai (1987). "Some classes of global Cramer–Rao bounds". Ann. Stat. 15 (4): 1421–38. doi:10.1214/aos/1176350602.
- ↑ Polyanskiy, Yury (2017). "Lecture notes on information theory, chapter 29, ECE563 (UIUC)". https://people.lids.mit.edu/yp/homepage/data/LN_stats.pdf.
- ↑ Kay, S. M. (1993). Fundamentals of Statistical Signal Processing: Estimation Theory. Prentice Hall. p. 47. ISBN 0-13-042268-1.
Further reading
- Amemiya, Takeshi (1985). Advanced Econometrics. Cambridge: Harvard University Press. pp. 14–17. ISBN 0-674-00560-0. https://archive.org/details/advancedeconomet00amem.
- Bos, Adriaan van den (2007). Parameter Estimation for Scientists and Engineers. Hoboken: John Wiley & Sons. pp. 45–98. ISBN 978-0-470-14781-8.
- Kay, Steven M. (1993). Fundamentals of Statistical Signal Processing, Volume I: Estimation Theory. Prentice Hall. ISBN 0-13-345711-7.. Chapter 3.
- Shao, Jun (1998). Mathematical Statistics. New York: Springer. ISBN 0-387-98674-X.. Section 3.1.3.
- Posterior uncertainty, asymptotic law and Cramér-Rao bound, Structural Control and Health Monitoring 25(1851):e2113 DOI: 10.1002/stc.2113
External links
- FandPLimitTool a GUI-based software to calculate the Fisher information and Cramér-Rao lower bound with application to single-molecule microscopy.
 |

