Database transaction schedule
In the fields of databases and transaction processing (transaction management), a schedule (or history) of a system is an abstract model to describe execution of transactions running in the system. Often it is a list of operations (actions) ordered by time, performed by a set of transactions that are executed together in the system. If the order in time between certain operations is not determined by the system, then a partial order is used. Examples of such operations are requesting a read operation, reading, writing, aborting, committing, requesting a lock, locking, etc. Not all transaction operation types should be included in a schedule, and typically only selected operation types (e.g., data access operations) are included, as needed to reason about and describe certain phenomena. Schedules and schedule properties are fundamental concepts in database concurrency control theory.
Formal description
The following is an example of a schedule:
| T1 | T2 | T3 |
|---|---|---|
| R(X) | ||
| W(X) | ||
| Com. | ||
| R(Y) | ||
| W(Y) | ||
| Com. | ||
| R(Z) | ||
| W(Z) | ||
| Com. |
In this example, the horizontal axis represents the different transactions in the schedule D. The vertical axis represents time order of operations. Schedule D consists of three transactions T1, T2, T3. The schedule describes the actions of the transactions as seen by the DBMS. First T1 Reads and Writes to object X, and then Commits. Then T2 Reads and Writes to object Y and Commits, and finally, T3 Reads and Writes to object Z and Commits. This is an example of a serial schedule, i.e., sequential with no overlap in time because the actions of all three transactions are sequential, and the transactions are not interleaved in time.
Representing the schedule D above by a table (rather than a list) is just for the convenience of identifying each transaction's operations in a glance. This notation is used throughout the article below. A more common way in the technical literature for representing such schedule is by a list:
- D = R1(X) W1(X) Com1 R2(Y) W2(Y) Com2 R3(Z) W3(Z) Com3
Usually, for the purpose of reasoning about concurrency control in databases, an operation is modelled as atomic, occurring at a point in time, without duration. When this is not satisfactory, start and end time-points and possibly other point events are specified (rarely). Real executed operations always have some duration and specified respective times of occurrence of events within them (e.g., "exact" times of beginning and completion), but for concurrency control reasoning usually only the precedence in time of the whole operations (without looking into the quite complex details of each operation) matters, i.e., which operation is before, or after another operation. Furthermore, in many cases, the before/after relationships between two specific operations do not matter and should not be specified, while being specified for other pairs of operations.
In general, operations of transactions in a schedule can interleave (i.e., transactions can be executed concurrently), while time orders between operations in each transaction remain unchanged as implied by the transaction's program. Since not always time orders between all operations of all transactions matter and need to be specified, a schedule is, in general, a partial order between operations rather than a total order (where order for each pair is determined, as in a list of operations). Also in the general case, each transaction may consist of several processes, and itself be properly represented by a partial order of operations, rather than a total order. Thus, in general, a schedule is a partial order of operations, containing (embedding) the partial orders of all its transactions.
Time-order between two operations can be represented by an ordered pair of these operations (e.g., the existence of a pair (OP1, OP2) means that OP1 is always before OP2), and a schedule in the general case is a set of such ordered pairs. Such a set, a schedule, is a partial order which can be represented by an acyclic directed graph (or directed acyclic graph, DAG) with operations as nodes and time-order as a directed edge (no cycles are allowed since a cycle means that a first (any) operation on a cycle can be both before and after (any) another second operation on the cycle, which contradicts our perception of Time). In many cases, a graphical representation of such a graph is used to demonstrate a schedule.
Comment: Since a list of operations (and the table notation used in this article) always represents a total order between operations, schedules that are not a total order cannot be represented by a list (but always can be represented by a DAG).
Types of schedule
A complete schedule is one that contains either an abort (a.k.a. rollback) or commit action for each of its transactions. A transaction's last action is either to commit or abort. To maintain atomicity, a transaction must undo all its actions if it is aborted.
Serial
The transactions are executed non-interleaved (i.e., a serial schedule is one in which no transaction starts until a running transaction has ended).
Schedule D is an example of a serial schedule:
| T1 | T2 | T3 |
|---|---|---|
| R(X) | ||
| W(X) | ||
| Com. | ||
| R(Y) | ||
| W(Y) | ||
| Com. | ||
| R(Z) | ||
| W(Z) | ||
| Com. |
Serializable
A schedule that is equivalent (in its outcome) to a serial schedule has the serializability property.
In schedule E, the order in which the actions of the transactions are executed is not the same as in D, but in the end, E gives the same result as D.
| T1 | T2 | T3 |
|---|---|---|
| R(X) | ||
| R(Y) | ||
| R(Z) | ||
| W(X) | ||
| W(Y) | ||
| W(Z) | ||
| Com. | Com. | Com. |
Serializability is used to keep the data in the data item in a consistent state. Serializability is a property of a transaction schedule (history). It is the major criterion for the correctness of concurrent transactions' schedule, and thus supported in all general purpose database systems. Schedules that are not serializable are likely to generate erroneous outcomes; which can be extremely harmful when dealing with money within banks.
If any specific order between some transactions is requested by an application, then it is enforced independently of the underlying serializability mechanisms. These mechanisms are typically indifferent to any specific order, and generate some unpredictable partial order that is typically compatible with multiple serial orders of these transactions. This partial order results from the scheduling orders of concurrent transactions' data access operations, which depend on many factors.
Serializability is used in concurrency control of databases,[1][2] transaction processing (transaction management), and various transactional applications (e.g., transactional memory[3] and software transactional memory). Transactions are normally executed concurrently (they overlap), since this is the most efficient way. Serializability is considered the highest level of isolation between transactions, and plays an essential role in concurrency control. As such it is supported in all general purpose database systems.
Serializability theory provides the formal framework to reason about and analyze serializability and its techniques. Though it is mathematical in nature, its fundamentals are informally (without mathematics notation) introduced below.
Conflicting actions
Two actions are said to be in conflict (conflicting pair) if and only if all of the 3 following conditions are satisfied:
- The actions belong to different transactions.
- At least one of the actions is a write operation.
- The actions access the same object (read or write).[4][5]
Equivalently, two actions are considered conflicting if and only if they are noncommutative. Equivalently, two actions are considered conflicting if and only if they are a read-write, write-read, or write-write conflict.
The following set of actions is conflicting:
- R1(X), W2(X), W3(X) (3 conflicting pairs)
While the following sets of actions are not conflicting:
- R1(X), R2(X), R3(X)
- R1(X), W2(Y), R3(X)
Reducing conflicts, such as through commutativity, enhances performance because conflicts are the fundamental cause of delays and aborts.
The conflict is materialized if the requested conflicting operation is actually executed: in many cases a requested/issued conflicting operation by a transaction is delayed and even never executed, typically by a lock on the operation's object, held by another transaction, or when writing to a transaction's temporary private workspace and materializing, copying to the database itself, upon commit; as long as a requested/issued conflicting operation is not executed upon the database itself, the conflict is non-materialized; non-materialized conflicts are not represented by an edge in the precedence graph.
Conflict equivalence
The schedules S1 and S2 are said to be conflict-equivalent if and only if both of the following two conditions are satisfied:
- Both schedules S1 and S2 involve the same set of transactions such that each transaction has the same actions in the same order.
- Both schedules have the same set of conflicting pairs (such that the actions in each conflicting pair are in the same order).[6] This is equivalent to requiring that all conflicting operations (i.e., operations in any conflicting pair) are in the same order in both schedules.
Equivalently, two schedules are said to be conflict equivalent if and only if one can be transformed to another by swapping pairs of non-conflicting operations (whether adjacent or not) while maintaining the order of actions for each transaction.[4]
Equivalently, two schedules are said to be conflict equivalent if and only if one can be transformed to another by swapping pairs of non-conflicting adjacent operations with different transactions.[7]
Conflict-serializable
A schedule is said to be conflict-serializable when the schedule is conflict-equivalent to one or more serial schedules.
Equivalently, a schedule is conflict-serializable if and only if its precedence graph is acyclic when only committed transactions are considered. Note that if the graph is defined to also include uncommitted transactions, then cycles involving uncommitted transactions may occur without conflict serializability violation.
The schedule K is conflict-equivalent to the serial schedule <T1,T2>, but not <T2,T1>.
| T1 | T2 |
|---|---|
| R(A) | |
| R(A) | |
| W(B) | |
| Com. | |
| W(A) | |
| Com. |
Conflict serializability can be enforced by restarting any transaction within the cycle in the precedence graph, or by implementing two-phase locking, timestamp ordering, or serializable snapshot isolation.[8]
Commitment-order-serializable
A schedule is said to be commitment-ordered (commit-ordered), or commitment-order-serializable, if it obeys the Commitment ordering (CO; also commit-ordering or commit-order-serializability) schedule property. This means that the order in time of transactions' commitment events is compatible with the precedence (partial) order of the respective transactions, as induced by their schedule's acyclic precedence graph (serializability graph, conflict graph). This implies that it is also conflict-serializable. The CO property is especially effective for achieving Global serializability in distributed systems.
Comment: Commitment ordering, which was discovered in 1990, is obviously not mentioned in (Bernstein et al. 1987). Its correct definition appears in (Weikum and Vossen 2001), however the description thereof its related techniques and theory is partial, inaccurate, and misleading.[according to whom?] For an extensive coverage of commitment ordering and its sources see Commitment ordering and The History of Commitment Ordering.
View equivalence
Two schedules S1 and S2 are said to be view-equivalent when the following conditions are satisfied:
- If the transaction in S1 reads an initial value for object X, so does the transaction in S2.
- If the transaction in S1 reads the value written by transaction in S1 for object X, so does the transaction in S2.
- If the transaction in S1 is the final transaction to write the value for an object X, so is the transaction in S2.
Additionally, two view-equivalent schedules must involve the same set of transactions such that each transaction has the same actions in the same order.
In the example below, the schedules S1 and S2 are view-equivalent, but they are not view-equivalent to S3.
| S1: T1 | S1: T2 | S2: T1 | S2: T2 | S3: T1 | S3: T2 |
|---|---|---|---|---|---|
| R(A) | R(A) | R(A) | |||
| W(A) | W(A) | W(A) | |||
| R(B) | R(A) | R(A) | |||
| W(B) | W(A) | W(A) | |||
| Com. | R(B) | R(B)(1) | |||
| R(A) | W(B) | W(B) | |||
| W(A) | Com. | R(B)(2) | |||
| R(B) | R(B) | W(B)(3) | |||
| W(B) | W(B) | Com. | |||
| Com. | Com. | Com. |
The conditions for view equivalence were not satisfied at the corresponding superscripts for the following reasons:
- Failed the first condition of view equivalence because T1 read the initial value for B in S1, but T2 read the initial value for B in S3.
- Failed the second condition of view equivalence because T2 read the value written by T1 for B in S1, but T1 read the value written by T2 for B in S3.
- Failed the third condition of view equivalence because T2 did the final write for B in S1, but T1 did the final write for B in S3.
To quickly analyze whether two schedules are view-equivalent, write both schedules as a list with each action's subscript representing which view-equivalence condition they match. The schedules are view equivalent if and only if all the actions have the same subscript (or lack thereof) in both schedules:
- S1: R1(A)initial read, W1(A), R1(B)initial read, W1(B), Com1, R2(A)written by T1, W2(A)final write, R2(B)written by T1, W2(B)final write, Com2
- S2: R1(A)initial read, W1(A), R2(A)written by T1, W2(A)final write, R1(B)initial read, W1(B), Com1, R2(B)written by T1, W2(B)final write, Com2
- S3: R1(A)initial read, W1(A), R2(A)written by T1, W2(A)final write, R2(B)initial read, W2(B), R1(B)written by T2, W1(B)final write, Com1, Com2
View-serializable
A schedule is view-serializable if it is view-equivalent to some serial schedule. Note that by definition, all conflict-serializable schedules are view-serializable.
| T1 | T2 |
|---|---|
| R(A) | |
| R(A) | |
| W(B) |
Notice that the above example (which is the same as the example in the discussion of conflict-serializable) is both view-serializable and conflict-serializable at the same time. There are however view-serializable schedules that are not conflict-serializable: those schedules with a transaction performing a blind write:
| T1 | T2 | T3 |
|---|---|---|
| R(A) | ||
| W(A) | ||
| Com. | ||
| W(A) | ||
| Com. | ||
| W(A) | ||
| Com. |
The above example is not conflict-serializable, but it is view-serializable since it has a view-equivalent serial schedule <T1,| T2,| T3>.
Since determining whether a schedule is view-serializable is NP-complete, view-serializability has little practical interest.[citation needed]
Relaxed serializability
Relaxed serializability allows controlled serializability violations in order to achieve higher performance. Higher performance means better transaction execution rate and shorter average transaction response time (transaction duration). Relaxed serializability is used when absolute correctness is not needed from recently modified data (such as when retrieving a list of products). Snapshot isolation is a common relaxed serializability method.
Relaxing distributed serializability is often necessary for efficient large-scale data replication because using a single atomic distributed transaction for synchronizing multiple replicas is likely to have unavailable computers and networks which would cause aborts.[9] Optimistic replication is a common distributed serializability relaxation method which compromises eventual consistency.
Classes of schedules defined by relaxed serializability properties either contain the serializability class, or are incomparable with it.
Distributed serializability
Distributed serializability is the serializability of a schedule of a transactional distributed system (e.g., a distributed database system). Such a system is characterized by distributed transactions (also called global transactions), i.e., transactions that span computer processes (a process abstraction in a general sense, depending on computing environment; e.g., operating system's thread) and possibly network nodes. A distributed transaction comprises more than one of several local sub-transactions that each has states as described above for a database transaction. A local sub-transaction comprises a single process, or more processes that typically fail together (e.g., in a single processor core). Distributed transactions imply a need for an atomic commit protocol to reach consensus among its local sub-transactions on whether to commit or abort. Such protocols can vary from a simple (one-phase) handshake among processes that fail together to more sophisticated protocols, like two-phase commit, to handle more complicated cases of failure (e.g., process, node, communication, etc. failure). Distributed serializability is a major goal of distributed concurrency control for correctness. With the proliferation of the Internet, cloud computing, grid computing, and small, portable, powerful computing devices (e.g., smartphones,) the need for effective distributed serializability techniques to ensure correctness in and among distributed applications seems to increase.
Distributed serializability is achieved by implementing distributed versions of the known centralized techniques.[10][11] Typically, all such distributed versions require utilizing conflict information (of either materialized or non-materialized conflicts, or, equivalently, transaction precedence or blocking information; conflict serializability is usually utilized) that is not generated locally, but rather in different processes, and remote locations. Thus information distribution is needed (e.g., precedence relations, lock information, timestamps, or tickets). When the distributed system is of a relatively small scale and message delays across the system are small, the centralized concurrency control methods can be used unchanged while certain processes or nodes in the system manage the related algorithms. However, in a large-scale system (e.g., grid and cloud), due to the distribution of such information, a substantial performance penalty is typically incurred, even when distributed versions of the methods (vs. the centralized ones) are used, primarily due to computer and communication latency. Also, when such information is distributed, related techniques typically do not scale well. A well-known example with respect to scalability problems is a distributed lock manager, which distributes lock (non-materialized conflict) information across the distributed system to implement locking techniques.
Recoverable
In a recoverable schedule, transactions only commit after all transactions whose changes they read have committed. A schedule becomes unrecoverable if a transaction reads and relies on changes from another transaction , and then commits and aborts.
| F: T1 | F: T2 | F2: T1 | F2: T2 | J: T1 | J: T2 |
|---|---|---|---|---|---|
| R(A) | R(A) | R(A) | |||
| W(A) | W(A) | W(A) | |||
| R(A) | R(A) | R(A) | |||
| W(A) | W(A) | W(A) | |||
| Com. | Abort | Com. | |||
| Com. | Abort | Abort |
These schedules are recoverable. The schedule F is recoverable because T1 commits before T2, that makes the value read by T2 correct. Then T2 can commit itself. In the F2 schedule, if T1 aborted, T2 has to abort because the value of A it read is incorrect. In both cases, the database is left in a consistent state.
Transaction J is unrecoverable because T2 committed before T1 despite previously reading the value written by T1. Because T1 aborted after T2 committed, the value read by T2 is wrong. Because a transaction cannot be rolled-back after it commits, the schedule is unrecoverable.
Cascadeless
Cascadeless schedules (a.k.a, "Avoiding Cascading Aborts (ACA) schedules") are schedules which avoid cascading aborts by disallowing dirty reads. Cascading aborts occur when one transaction's abort causes another transaction to abort because it read and relied on the first transaction's changes to an object. A dirty read occurs when a transaction reads data from uncommitted write in another transaction.[12]
The following examples are the same as the ones in the discussion on recoverable:
| F: T1 | F: T2 | F2: T1 | F2: T2 |
|---|---|---|---|
| R(A) | R(A) | ||
| W(A) | W(A) | ||
| R(A) | R(A) | ||
| W(A) | W(A) | ||
| Com. | Abort | ||
| Com. | Abort |
In this example, although F2 is recoverable, it does not avoid cascading aborts. It can be seen that if T1 aborts, T2 will have to be aborted too in order to maintain the correctness of the schedule as T2 has already read the uncommitted value written by T1.
The following is a recoverable schedule which avoids cascading abort. Note, however, that the update of A by T1 is always lost (since T1 is aborted).
| T1 | T2 |
|---|---|
| R(A) | |
| R(A) | |
| W(A) | |
| W(A) | |
| Abort | |
| Commit |
Note that this Schedule would not be serializable if T1 would be committed. Cascading aborts avoidance is sufficient but not necessary for a schedule to be recoverable.
Strict
A schedule is strict - has the strictness property - if for any two transactions T1, T2, if a write operation of T1 precedes a conflicting operation of T2 (either read or write), then the commit or abort event of T1 also precedes that conflicting operation of T2.
Any strict schedule is cascade-less, but not the converse. Strictness allows efficient recovery of databases from failure.
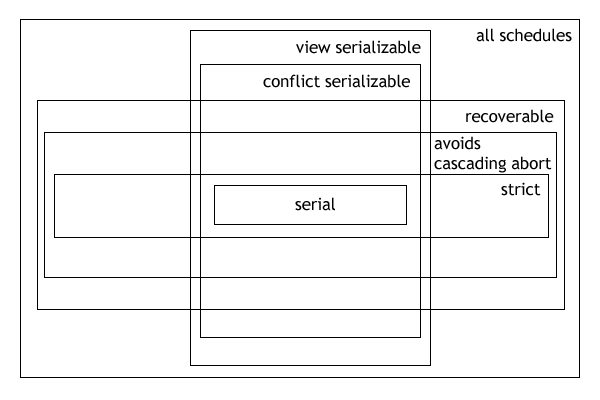
Hierarchical relationship between serializability classes
The following expressions illustrate the hierarchical (containment) relationships between serializability and recoverability classes:
- Serial ⊂ commitment-ordered ⊂ conflict-serializable ⊂ view-serializable ⊂ all schedules
- Serial ⊂ strict ⊂ cascadeless (ACA) ⊂ recoverable ⊂ all schedules
The Venn diagram (below) illustrates the above clauses graphically.
Practical implementations
In practice, most general purpose database systems employ conflict-serializable and recoverable (primarily strict) schedules.
See also
- schedule (project management)
- Strong strict two-phase locking (SS2PL or Rigorousness).
- Making snapshot isolation serializable[13] in Snapshot isolation.
- Global serializability, where the Global serializability problem and its proposed solutions are described.
- Linearizability, a more general concept in concurrent computing.
References
- ↑ Philip A. Bernstein, Vassos Hadzilacos, Nathan Goodman (1987): Concurrency Control and Recovery in Database Systems (free PDF download), Addison Wesley Publishing Company, ISBN 0-201-10715-5
- ↑ Gerhard Weikum, Gottfried Vossen (2001): Transactional Information Systems, Elsevier, ISBN 1-55860-508-8
- ↑ Maurice Herlihy and J. Eliot B. Moss. Transactional memory: architectural support for lock-free data structures. Proceedings of the 20th annual international symposium on Computer architecture (ISCA '93). Volume 21, Issue 2, May 1993.
- ↑ 4.0 4.1 "Conflict Serializability in DBMS" (in en-US). 2015-12-29. https://www.geeksforgeeks.org/conflict-serializability-in-dbms/.
- ↑ Silberschatz, Abraham; Korth, Henry F.; Sudarshan, S. (2020). Database system concepts (Seventh ed.). New York, NY: McGraw-Hill Education. pp. 814. ISBN 978-1-260-08450-4.
- ↑ Ramakrishnan, Raghu; Gehrke, Johannes (2000). Database management systems. Computer science series (2nd ed.). Boston: McGraw-Hill. pp. 540. ISBN 978-0-07-232206-4.
- ↑ Garcia-Molina, Hector; Ullman, Jeffrey D.; Widom, Jennifer (2009). Database systems: the complete book. Pearson international edition (2nd ed.). Upper Saddle River, NJ: Pearson/Prentice Hall. pp. 891-892. ISBN 978-0-13-187325-4.
- ↑ Michael J. Cahill, Uwe Röhm, Alan D. Fekete (2008): "Serializable isolation for snapshot databases", Proceedings of the 2008 ACM SIGMOD international conference on Management of data, pp. 729-738, Vancouver, Canada, June 2008, ISBN 978-1-60558-102-6 (SIGMOD 2008 best paper award)
- ↑ Gray, J.; Helland, P.; O’Neil, P.; Shasha, D. (1996). "The dangers of replication and a solution". Proceedings of the 1996 ACM SIGMOD International Conference on Management of Data. pp. 173–182. doi:10.1145/233269.233330. ftp://ftp.research.microsoft.com/pub/tr/tr-96-17.pdf.[yes|permanent dead link|dead link}}]
- ↑ Philip A. Bernstein, Vassos Hadzilacos, Nathan Goodman (1987): Concurrency Control and Recovery in Database Systems (free PDF download), Addison Wesley Publishing Company, ISBN 0-201-10715-5
- ↑ Gerhard Weikum, Gottfried Vossen (2001): Transactional Information Systems, Elsevier, ISBN 1-55860-508-8
- ↑ "Cascadeless in DBMS" (in en-US). 2019-08-06. https://www.geeksforgeeks.org/cascadeless-in-dbms/.
- ↑ Michael J. Cahill, Uwe Röhm, Alan D. Fekete (2008): "Serializable isolation for snapshot databases", Proceedings of the 2008 ACM SIGMOD international conference on Management of data, pp. 729-738, Vancouver, Canada, June 2008, ISBN 978-1-60558-102-6 (SIGMOD 2008 best paper award)
- Philip A. Bernstein, Vassos Hadzilacos, Nathan Goodman: Concurrency Control and Recovery in Database Systems, Addison Wesley Publishing Company, 1987, ISBN 0-201-10715-5
- Gerhard Weikum, Gottfried Vossen: Transactional Information Systems, Elsevier, 2001, ISBN 1-55860-508-8
 |
