Datasaurus dozen
| Part of a series on Statistics |
| Data visualization |
|---|
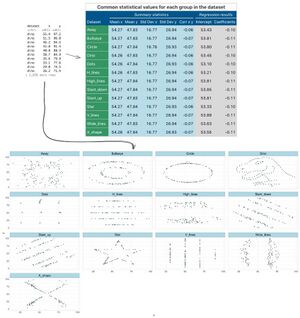
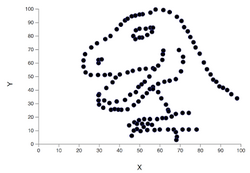
The Datasaurus dozen comprises thirteen data sets that have nearly identical simple descriptive statistics to two decimal places, yet have very different distributions and appear very different when graphed.[1] It was inspired by the smaller Anscombe's quartet that was created in 1973.
Data
For all thirteen data sets:
| Property | Value | Accuracy |
|---|---|---|
| Number of elements | 142 | exact |
| Mean of x | 54.26 | to 2 decimal places |
| Sample variance of x: s2x | 16.76 | to 2 decimal places |
| Mean of y | 47.83 | to 2 decimal places |
| Sample variance of y: s2y | 26.93 | to 2 decimal places |
| Correlation between x and y | -0.06 | to 3 decimal places |
| Linear regression line | y = 53 - 0.1x | to 0 and 1 decimal places, respectively |
| Coefficient of determination of the linear regression: [math]\displaystyle{ R^2 }[/math] | 0.004 | to 3 decimal places |
The thirteen data sets were labeled as the following:
- away
- bullseye
- circle
- dino
- dots
- h_lines
- high_lines
- slant_down
- slant_up
- star
- v_line
- wide_lines
- x_shape
Similar to the Anscombe's quartet, the Datasaurus dozen was designed to further illustrate the importance of looking at a set of data graphically before starting to analyze according to a particular type of relationship, and the inadequacy of basic statistic properties for describing realistic datasets.[2][3][4][5][1][6]
Creation
The initial "datasaurus" dataset was constructed in 2016 by Alberto Cairo.[7] It was proposed by Maarten Lambrechts that this dataset also be called "Anscombosaurus".[7]
This dataset was then accompanied by twelve other datasets that were created by Justin Matejka and George Fitzmaurice at Autodesk. Unlike the Anscombe's quartet where it is not known how the data set was generated,[8] it is known that the authors used simulated annealing to make these data sets. They made small, random, and biased changes to each point towards the desired shape. Each shape took 200,000 iterations of perturbations to complete.[1]
The pseudocode for this algorithm is as follows:
current_ds ← initial_ds
for x iterations, do:
test_ds ← perturb(current_ds, temp)
if similar_enough(test_ds, initial_ds):
current_ds ← test_ds
function perturb(ds, temp):
loop:
test ← move_random_points(ds)
if fit(test) > fit(ds) or temp > random():
return test
where
initial_dsis the seed datasetcurrent_dsis the latest version of the datasetfit()is a function used to check whether moving the points gets closer to the desired shapetempis the temperature of the simulated annealing algorithm0similar_enough()is a function that checks whether the statistics for the two given datasets are similar enoughmove_random_points()is a function that randomly moves data points
See also
- Exploratory data analysis
- Goodness of fit
- Regression validation
- Simpson's paradox
- Statistical model validation
- Anscombe's quartet
References
- ↑ 1.0 1.1 1.2 Matejka, Justin; Fitzmaurice, George (2017-05-02). "Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing". Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems. CHI '17 (New York, NY, USA: Association for Computing Machinery): 1290–1294. doi:10.1145/3025453.3025912. ISBN 978-1-4503-4655-9. https://doi.org/10.1145/3025453.3025912.
- ↑ Elert, Glenn (2021). "Linear Regression". The Physics Hypertextbook. http://physics.info/linear-regression/practice.shtml#4.
- ↑ Janert, Philipp K. (2010). Data Analysis with Open Source Tools. O'Reilly Media. pp. 65–66. ISBN 978-0-596-80235-6. https://archive.org/details/isbn_9780596802356/page/65.
- ↑ Chatterjee, Samprit; Hadi, Ali S. (2006). Regression Analysis by Example. John Wiley and Sons. p. 91. ISBN 0-471-74696-7.
- ↑ Saville, David J.; Wood, Graham R. (1991). Statistical Methods: The geometric approach. Springer. p. 418. ISBN 0-387-97517-9.
- ↑ Tufte, Edward R. (2001). The Visual Display of Quantitative Information (2nd ed.). Cheshire, CT: Graphics Press. ISBN 0-9613921-4-2. https://archive.org/details/visualdisplayofq00tuft.
- ↑ 7.0 7.1 Cairo, Alberto. "Download the Datasaurus: Never trust summary statistics alone; always visualize your data". http://www.thefunctionalart.com/2016/08/download-datasaurus-never-trust-summary.html.
- ↑ Chatterjee, Sangit; Firat, Aykut (2007). "Generating Data with Identical Statistics but Dissimilar Graphics: A follow up to the Anscombe dataset". The American Statistician 61 (3): 248–254. doi:10.1198/000313007X220057.
External links
- Animated examples from Autodesk for the Datasaurus Dozen datasets
- datasauRus, datasets from the Datasaurus Dozen in R
- The Datasaurus Dozen in CSV and tab-delimited files https://www.openintro.org/data/index.php?data=datasaurus
 |