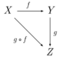Exponential object

Short description: Categorical generalization of a function space in set theory

In mathematics, specifically in category theory, an exponential object or map object is the categorical generalization of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories. Categories (such as subcategories of Top) without adjoined products may still have an exponential law.

Definition

Let [math]\displaystyle{ \mathbf{C} }[/math] be a category, let [math]\displaystyle{ Z }[/math] and [math]\displaystyle{ Y }[/math] be objects of [math]\displaystyle{ \mathbf{C} }[/math], and let [math]\displaystyle{ \mathbf{C} }[/math] have all binary products with [math]\displaystyle{ Y }[/math]. An object [math]\displaystyle{ Z^Y }[/math] together with a morphism [math]\displaystyle{ \mathrm{eval}\colon (Z^Y \times Y) \to Z }[/math] is an exponential object if for any object [math]\displaystyle{ X }[/math] and morphism [math]\displaystyle{ g \colon X\times Y \to Z }[/math] there is a unique morphism [math]\displaystyle{ \lambda g\colon X\to Z^Y }[/math] (called the transpose of [math]\displaystyle{ g }[/math]) such that the following diagram commutes:

This assignment of a unique [math]\displaystyle{ \lambda g }[/math] to each [math]\displaystyle{ g }[/math] establishes an isomorphism (bijection) of hom-sets, [math]\displaystyle{ \mathrm{Hom}(X\times Y,Z) \cong \mathrm{Hom}(X,Z^Y). }[/math]

If [math]\displaystyle{ Z^Y }[/math]exists for all objects [math]\displaystyle{ Z, Y }[/math] in [math]\displaystyle{ \mathbf{C} }[/math], then the functor [math]\displaystyle{ (-)^Y \colon \mathbf{C}\to \mathbf{C} }[/math] defined on objects by [math]\displaystyle{ Z \mapsto Z^Y }[/math] and on arrows by [math]\displaystyle{ (f\colon X\to Z) \mapsto (f^Y\colon X^Y \to Z^Y) }[/math], is a right adjoint to the product functor [math]\displaystyle{ -\times Y }[/math]. For this reason, the morphisms [math]\displaystyle{ \lambda g }[/math] and [math]\displaystyle{ g }[/math] are sometimes called exponential adjoints of one another.

Equational definition

Alternatively, the exponential object may be defined through equations:

• Existence of [math]\displaystyle{ \lambda g }[/math] is guaranteed by existence of the operation [math]\displaystyle{ \lambda - }[/math].
• Commutativity of the diagrams above is guaranteed by the equality [math]\displaystyle{ \forall g \colon X \times Y \to Z,\ \mathrm{eval} \circ (\lambda g \times \mathrm{id}_Y) = g }[/math].
• Uniqueness of [math]\displaystyle{ \lambda g }[/math] is guaranteed by the equality [math]\displaystyle{ \forall h \colon X \to Z^Y, \ \lambda (\mathrm{eval} \circ (h \times \mathrm{id}_Y)) = h }[/math].

Universal property

The exponential [math]\displaystyle{ Z^Y }[/math] is given by a universal morphism from the product functor [math]\displaystyle{ - \times Y }[/math] to the object [math]\displaystyle{ Z }[/math]. This universal morphism consists of an object [math]\displaystyle{ Z^Y }[/math] and a morphism [math]\displaystyle{ \mathrm{eval}\colon (Z^Y \times Y) \to Z }[/math].

Examples

In the category of sets, an exponential object [math]\displaystyle{ Z^Y }[/math] is the set of all functions [math]\displaystyle{ Y \to Z }[/math]. The map [math]\displaystyle{ \mathrm{eval}\colon (Z^Y \times Y) \to Z }[/math] is just the evaluation map, which sends the pair [math]\displaystyle{ (f, y) }[/math] to [math]\displaystyle{ f(y) }[/math]. For any map [math]\displaystyle{ g\colon X \times Y \to Z }[/math] the map [math]\displaystyle{ \lambda g\colon X \to Z^Y }[/math] is the curried form of [math]\displaystyle{ g }[/math]:

[math]\displaystyle{ \lambda g(x)(y) = g(x,y).\, }[/math]

A Heyting algebra [math]\displaystyle{ H }[/math] is just a bounded lattice that has all exponential objects. Heyting implication, [math]\displaystyle{ Y \Rightarrow Z }[/math], is an alternative notation for [math]\displaystyle{ Z^Y }[/math]. The above adjunction results translate to implication ([math]\displaystyle{ \Rightarrow : H \times H \to H }[/math]) being right adjoint to meet ([math]\displaystyle{ \wedge : H \times H \to H }[/math]). This adjunction can be written as [math]\displaystyle{ (- \wedge Y) \dashv (Y \Rightarrow -) }[/math], or more fully as: [math]\displaystyle{ (- \wedge Y): H \stackrel {\longrightarrow} {\underset {\longleftarrow}{\top}} H: (Y \Rightarrow -) }[/math]

In the category of topological spaces, the exponential object [math]\displaystyle{ Z^Y }[/math] exists provided that [math]\displaystyle{ Y }[/math] is a locally compact Hausdorff space. In that case, the space [math]\displaystyle{ Z^Y }[/math] is the set of all continuous functions from [math]\displaystyle{ Y }[/math] to [math]\displaystyle{ Z }[/math] together with the compact-open topology. The evaluation map is the same as in the category of sets; it is continuous with the above topology. If [math]\displaystyle{ Y }[/math] is not locally compact Hausdorff, the exponential object may not exist (the space [math]\displaystyle{ Z^Y }[/math] still exists, but it may fail to be an exponential object since the evaluation function need not be continuous). For this reason the category of topological spaces fails to be cartesian closed. However, the category of locally compact topological spaces is not cartesian closed either, since [math]\displaystyle{ Z^Y }[/math] need not be locally compact for locally compact spaces [math]\displaystyle{ Z }[/math] and [math]\displaystyle{ Y }[/math]. A cartesian closed category of spaces is, for example, given by the full subcategory spanned by the compactly generated Hausdorff spaces.

In functional programming languages, the morphism [math]\displaystyle{ \operatorname{eval} }[/math] is often called [math]\displaystyle{ \operatorname{apply} }[/math], and the syntax [math]\displaystyle{ \lambda g }[/math] is often written [math]\displaystyle{ \operatorname{curry}(g) }[/math]. The morphism [math]\displaystyle{ \operatorname{eval} }[/math] here must not to be confused with the eval function in some programming languages, which evaluates quoted expressions.

See also

• Closed monoidal category

References

• Adámek, Jiří; Horst Herrlich; George Strecker (2006). Abstract and Concrete Categories (The Joy of Cats). John Wiley & Sons. http://katmat.math.uni-bremen.de/acc/. 
• Awodey, Steve (2010). "Chapter 6: Exponentials". Category theory. Oxford New York: Oxford University Press. ISBN 978-0199237180. 
• Mac Lane, Saunders (1998). "Chapter 4: Adjoints". Categories for the working mathematician. New York: Springer. ISBN 978-0387984032. 

External links

• Interactive Web page which generates examples of exponential objects and other categorical constructions. Written by Jocelyn Paine.