Folded normal distribution

Short description: Probability distribution

Probability density function 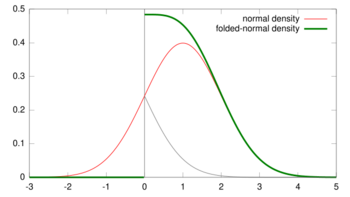μ=1, σ=1
Cumulative distribution function μ=1, σ=1
Parameters	μ ∈ R   (location) σ2 > 0   (scale)
Support	x ∈ [0,∞)
PDF	$\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}+\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x+\mu {)}^2}{2{\sigma }^2}}$
CDF	$\frac{1}{2}[\text{erf}\left(\frac{x+\mu }{\sigma \sqrt{2}}\right)+\text{erf}\left(\frac{x-\mu }{\sigma \sqrt{2}}\right)]$
Mean	${\mu }_Y=\sigma \sqrt{\frac{2}{\pi }}{e}^{(-{\mu }^2/2{\sigma }^2)}+\mu (1-2\mathrm{\Phi }(-\frac{\mu }{\sigma }))$
Variance	${\sigma }_Y^2={\mu }^2+{\sigma }^2-{\mu }_Y^2$

The folded normal distribution is a probability distribution related to the normal distribution. Given a normally distributed random variable X with mean μ and variance σ², the random variable Y = |X| has a folded normal distribution. Such a case may be encountered if only the magnitude of some variable is recorded, but not its sign. The distribution is called "folded" because probability mass to the left of x = 0 is folded over by taking the absolute value. In the physics of heat conduction, the folded normal distribution is a fundamental solution of the heat equation on the half space; it corresponds to having a perfect insulator on a hyperplane through the origin.

Definitions

Density

The probability density function (PDF) is given by

$f_Y(x;\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}+\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{(x+\mu {)}^2}{2{\sigma }^2}}$

for x ≥ 0, and 0 everywhere else. An alternative formulation is given by

$f\left(x\right)=\sqrt{\frac{2}{\pi {\sigma }^2}}{e}^{-\frac{(x^2+{\mu }^2)}{2{\sigma }^2}}\cosh \left(\frac{\mu x}{{\sigma }^2}\right)$,

where cosh is the cosine Hyperbolic function. It follows that the cumulative distribution function (CDF) is given by:

$F_Y(x;\mu ,{\sigma }^2)=\frac{1}{2}[\text{erf}\left(\frac{x+\mu }{\sqrt{2{\sigma }^2}}\right)+\text{erf}\left(\frac{x-\mu }{\sqrt{2{\sigma }^2}}\right)]$

for x ≥ 0, where erf() is the error function. This expression reduces to the CDF of the half-normal distribution when μ = 0.

The mean of the folded distribution is then

${\mu }_Y=\sigma \sqrt{\frac{2}{\pi }}\exp \left(\frac{-{\mu }^2}{2{\sigma }^2}\right)+\mu \text{erf}\left(\frac{\mu }{\sqrt{2{\sigma }^2}}\right)$

or

${\mu }_Y=\sqrt{\frac{2}{\pi }}\sigma e^{-\frac{{\mu }^2}{2{\sigma }^2}}+\mu [1-2\mathrm{\Phi }(-\frac{\mu }{\sigma })]$

where $\mathrm{\Phi }$ is the normal cumulative distribution function:

$\mathrm{\Phi }(x)=\frac{1}{2}[1+\mathrm{erf}\left(\frac{x}{\sqrt{2}}\right)].$

The variance then is expressed easily in terms of the mean:

${\sigma }_Y^2={\mu }^2+{\sigma }^2-{\mu }_Y^2.$

Both the mean (μ) and variance (σ²) of X in the original normal distribution can be interpreted as the location and scale parameters of Y in the folded distribution.

Properties

Mode

The mode of the distribution is the value of $x$ for which the density is maximised. In order to find this value, we take the first derivative of the density with respect to $x$ and set it equal to zero. Unfortunately, there is no closed form. We can, however, write the derivative in a better way and end up with a non-linear equation

$\frac{df(x)}{dx}=0\Rightarrow -\frac{(x-\mu )}{{\sigma }^2}{e}^{-\frac{1}{2}\frac{{(x-\mu )}^2}{{\sigma }^2}}-\frac{(x+\mu )}{{\sigma }^2}{e}^{-\frac{1}{2}\frac{{(x+\mu )}^2}{{\sigma }^2}}=0$

$x[e^{-\frac{1}{2}\frac{{(x-\mu )}^2}{{\sigma }^2}}+e^{-\frac{1}{2}\frac{{(x+\mu )}^2}{{\sigma }^2}}]-\mu [e^{-\frac{1}{2}\frac{{(x-\mu )}^2}{{\sigma }^2}}-e^{-\frac{1}{2}\frac{{(x+\mu )}^2}{{\sigma }^2}}]=0$

$x(1+e^{-\frac{2\mu x}{{\sigma }^2}})-\mu (1-e^{-\frac{2\mu x}{{\sigma }^2}})=0$

$(\mu +x)e^{-\frac{2\mu x}{{\sigma }^2}}=\mu -x$

$x=-\frac{{\sigma }^2}{2\mu }\log \frac{\mu -x}{\mu +x}$.

Tsagris et al. (2014) saw from numerical investigation that when

$\mu <\sigma$

, the maximum is met when

$x=0$

, and when

$\mu$

becomes greater than

$3\sigma$

, the maximum approaches

$\mu$

. This is of course something to be expected, since, in this case, the folded normal converges to the normal distribution. In order to avoid any trouble with negative variances, the exponentiation of the parameter is suggested. Alternatively, you can add a constraint, such as if the optimiser goes for a negative variance the value of the log-likelihood is NA or something very small.

Characteristic function and other related functions

• The characteristic function is given by

${\phi }_x\left(t\right)=e^{\frac{-{\sigma }^2{t}^2}{2}+i\mu t}\mathrm{\Phi }(\frac{\mu }{\sigma }+i\sigma t)+e^{-\frac{{\sigma }^2{t}^2}{2}-i\mu t}\mathrm{\Phi }(-\frac{\mu }{\sigma }+i\sigma t)$.

• The moment generating function is given by

$M_x\left(t\right)={\phi }_x(-it)=e^{\frac{{\sigma }^2{t}^2}{2}+\mu t}\mathrm{\Phi }(\frac{\mu }{\sigma }+\sigma t)+e^{\frac{{\sigma }^2{t}^2}{2}-\mu t}\mathrm{\Phi }(-\frac{\mu }{\sigma }+\sigma t)$.

• The cumulant generating function is given by

$K_x\left(t\right)=\log M_x\left(t\right)=(\frac{{\sigma }^2{t}^2}{2}+\mu t)+\log \{1-\mathrm{\Phi }(-\frac{\mu }{\sigma }-\sigma t)+e^{\frac{{\sigma }^2{t}^2}{2}-\mu t}[1-\mathrm{\Phi }(\frac{\mu }{\sigma }-\sigma t)]\}$.

• The Laplace transformation is given by

$E\left(e^{-tx}\right)=e^{\frac{{\sigma }^2{t}^2}{2}-\mu t}[1-\mathrm{\Phi }(-\frac{\mu }{\sigma }+\sigma t)]+e^{\frac{{\sigma }^2{t}^2}{2}+\mu t}[1-\mathrm{\Phi }(\frac{\mu }{\sigma }+\sigma t)]$.

• The Fourier transform is given by

$\hat{f}\left(t\right)={\phi }_x(-2\pi t)=e^{\frac{-4{\pi }^2{\sigma }^2{t}^2}{2}-i2\pi \mu t}[1-\mathrm{\Phi }(-\frac{\mu }{\sigma }-i2\pi \sigma t)]+e^{-\frac{4{\pi }^2{\sigma }^2{t}^2}{2}+i2\pi \mu t}[1-\mathrm{\Phi }(\frac{\mu }{\sigma }-i2\pi \sigma t)]$.

Related distributions

• When μ = 0, the distribution of Y is a half-normal distribution.
• The random variable (Y/σ)² has a noncentral chi-squared distribution with 1 degree of freedom and noncentrality equal to (μ/σ)².
• The folded normal distribution can also be seen as the limit of the folded non-standardized t distribution as the degrees of freedom go to infinity.
• There is a bivariate version developed by Psarakis and Panaretos (2001) as well as a multivariate version developed by Chakraborty and Chatterjee (2013).
• The Rice distribution is a multivariate generalization of the folded normal distribution.
• Modified half-normal distribution with the pdf on $(0,\mathrm{\infty })$ is given as $f(x)=\frac{2{\beta }^{\frac{\alpha }{2}}{x}^{\alpha -1}\exp (-\beta x^2+\gamma x)}{\mathrm{\Psi }(\frac{\alpha }{2},\frac{\gamma }{\sqrt{\beta }})}$, where $\mathrm{\Psi }(\alpha ,z)={}_1{\mathrm{\Psi }}_1(\begin{array}{c}(\alpha ,\frac{1}{2})\\ (1,0)\end{array};z)$ denotes the Fox–Wright Psi function.

Statistical Inference

Estimation of parameters

There are a few ways of estimating the parameters of the folded normal. All of them are essentially the maximum likelihood estimation procedure, but in some cases, a numerical maximization is performed, whereas in other cases, the root of an equation is being searched. The log-likelihood of the folded normal when a sample $x_i$ of size $n$ is available can be written in the following way

$l=-\frac{n}{2}\log 2\pi {\sigma }^2+\sum _{i=1}^n\log [e^{-\frac{{(x_i-\mu )}^2}{2{\sigma }^2}}+e^{-\frac{{(x_i+\mu )}^2}{2{\sigma }^2}}]$

$l=-\frac{n}{2}\log 2\pi {\sigma }^2+\sum _{i=1}^n\log \left[e^{-\frac{{(x_i-\mu )}^2}{2{\sigma }^2}}(1+e^{-\frac{{(x_i+\mu )}^2}{2{\sigma }^2}}{e}^{\frac{{(x_i-\mu )}^2}{2{\sigma }^2}})\right]$

$l=-\frac{n}{2}\log 2\pi {\sigma }^2-\sum _{i=1}^n\frac{{(x_i-\mu )}^2}{2{\sigma }^2}+\sum _{i=1}^n\log (1+e^{-\frac{2\mu x_i}{{\sigma }^2}})$

In R (programming language), using the package Rfast one can obtain the MLE really fast (command foldnorm.mle). Alternatively, the command optim or nlm will fit this distribution. The maximisation is easy, since two parameters (

$\mu$

and

${\sigma }^2$

) are involved. Note, that both positive and negative values for

$\mu$

are acceptable, since

$\mu$

belongs to the real line of numbers, hence, the sign is not important because the distribution is symmetric with respect to it. The next code is written in R

folded <- function(y) {

  ## y is a vector with positive data
  n <- length(y)  ## sample size
  sy2 <- sum(y^2)

    sam <- function(para, n, sy2) {
      me <- para[1]   ;   se <- exp( para[2] )
      f <-  - n/2 * log(2/pi/se) + n * me^2 / 2 / se +
            sy2 / 2 / se - sum( log( cosh( me * y/se ) ) )
      f
    }

  mod <- optim( c( mean(y), sd(y) ), n = n, sy2 = sy2, sam, control = list(maxit = 2000) )
  mod <- optim( mod$par, sam, n = n, sy2 = sy2, control = list(maxit = 20000) )
  result <- c( -mod$value, mod$par[1], exp(mod$par[2]) )
  names(result) <- c("log-likelihood", "mu", "sigma squared")
  result

}

The partial derivatives of the log-likelihood are written as

$\frac{\partial l}{\partial \mu }=\frac{\sum _{i=1}^n(x_i-\mu )}{{\sigma }^2}-\frac{2}{{\sigma }^2}\sum _{i=1}^n\frac{x_i{e}^{\frac{-2\mu x_i}{{\sigma }^2}}}{1+e^{\frac{-2\mu x_i}{{\sigma }^2}}}$

$\frac{\partial l}{\partial \mu }=\frac{\sum _{i=1}^n(x_i-\mu )}{{\sigma }^2}-\frac{2}{{\sigma }^2}\sum _{i=1}^n\frac{x_i}{1+e^{\frac{2\mu x_i}{{\sigma }^2}}}\text{and}$

$\frac{\partial l}{\partial {\sigma }^2}=-\frac{n}{2{\sigma }^2}+\frac{\sum _{i=1}^n{(x_i-\mu )}^2}{2{\sigma }^4}+\frac{2\mu }{{\sigma }^4}\sum _{i=1}^n\frac{x_i{e}^{-\frac{2\mu x_i}{{\sigma }^2}}}{1+e^{-\frac{2\mu x_i}{{\sigma }^2}}}$

$\frac{\partial l}{\partial {\sigma }^2}=-\frac{n}{2{\sigma }^2}+\frac{\sum _{i=1}^n{(x_i-\mu )}^2}{2{\sigma }^4}+\frac{2\mu }{{\sigma }^4}\sum _{i=1}^n\frac{x_i}{1+e^{\frac{2\mu x_i}{{\sigma }^2}}}$.

By equating the first partial derivative of the log-likelihood to zero, we obtain a nice relationship

$\sum _{i=1}^n\frac{x_i}{1+e^{\frac{2\mu x_i}{{\sigma }^2}}}=\frac{\sum _{i=1}^n(x_i-\mu )}{2}$.

Note that the above equation has three solutions, one at zero and two more with the opposite sign. By substituting the above equation, to the partial derivative of the log-likelihood w.r.t ${\sigma }^2$ and equating it to zero, we get the following expression for the variance

${\sigma }^2=\frac{\sum _{i=1}^n{(x_i-\mu )}^2}{n}+\frac{2\mu \sum _{i=1}^n(x_i-\mu )}{n}=\frac{\sum _{i=1}^n(x_i^2-{\mu }^2)}{n}=\frac{\sum _{i=1}^n{x}_i^2}{n}-{\mu }^2$,

which is the same formula as in the normal distribution. A main difference here is that $\mu$ and ${\sigma }^2$ are not statistically independent. The above relationships can be used to obtain maximum likelihood estimates in an efficient recursive way. We start with an initial value for ${\sigma }^2$ and find the positive root ($\mu$) of the last equation. Then, we get an updated value of ${\sigma }^2$. The procedure is being repeated until the change in the log-likelihood value is negligible. Another easier and more efficient way is to perform a search algorithm. Let us write the last equation in a more elegant way

$2\sum _{i=1}^n\frac{x_i}{1+e^{\frac{2\mu x_i}{{\sigma }^2}}}-\sum _{i=1}^n\frac{x_i(1+e^{\frac{2\mu x_i}{{\sigma }^2}})}{1+e^{\frac{2\mu x_i}{{\sigma }^2}}}+n\mu =0$

$\sum _{i=1}^n\frac{x_i(1-e^{\frac{2\mu x_i}{{\sigma }^2}})}{1+e^{\frac{2\mu x_i}{{\sigma }^2}}}+n\mu =0$.

It becomes clear that the optimization the log-likelihood with respect to the two parameters has turned into a root search of a function. This of course is identical to the previous root search. Tsagris et al. (2014) spotted that there are three roots to this equation for $\mu$, i.e. there are three possible values of $\mu$ that satisfy this equation. The $-\mu$ and $+\mu$, which are the maximum likelihood estimates and 0, which corresponds to the minimum log-likelihood.

See also

• Folded cumulative distribution
• Half-normal distribution
• Modified half-normal distribution with the pdf on $(0,\mathrm{\infty })$ is given as $f(x)=\frac{2{\beta }^{\frac{\alpha }{2}}{x}^{\alpha -1}\exp (-\beta x^2+\gamma x)}{\mathrm{\Psi }(\frac{\alpha }{2},\frac{\gamma }{\sqrt{\beta }})}$, where $\mathrm{\Psi }(\alpha ,z)={}_1{\mathrm{\Psi }}_1(\begin{array}{c}(\alpha ,\frac{1}{2})\\ (1,0)\end{array};z)$ denotes the Fox–Wright Psi function.
• Truncated normal distribution

References

• Tsagris, M.; Beneki, C.; Hassani, H. (2014). "On the folded normal distribution". Mathematics 2 (1): 12–28. doi:10.3390/math2010012. 
• "The Folded Normal Distribution". Technometrics 3 (4): 543–550. 1961. doi:10.2307/1266560. 
• Johnson NL (1962). "The folded normal distribution: accuracy of the estimation by maximum likelihood". Technometrics 4 (2): 249–256. doi:10.2307/1266622. 
• Nelson LS (1980). "The Folded Normal Distribution". J Qual Technol 12 (4): 236–238. doi:10.1080/00224065.1980.11980971. 
• Elandt RC (1961). "The folded normal distribution: two methods of estimating parameters from moments". Technometrics 3 (4): 551–562. doi:10.2307/1266561. 
• Lin PC (2005). "Application of the generalized folded-normal distribution to the process capability measures". Int J Adv Manuf Technol 26 (7–8): 825–830. doi:10.1007/s00170-003-2043-x. 
• Psarakis, S.; Panaretos, J. (1990). "The folded t distribution". Communications in Statistics - Theory and Methods 19 (7): 2717–2734. doi:10.1080/03610929008830342. 
• Psarakis, S.; Panaretos, J. (2001). "On some bivariate extensions of the folded normal and the folded-t distributions". Journal of Applied Statistical Science 10 (2): 119–136. 
• Chakraborty, A. K.; Chatterjee, M. (2013). "On multivariate folded normal distribution". Sankhyā: The Indian Journal of Statistics, Series B 75 (1): 1–15. 

External links

• Random (formerly Virtual Laboratories): The Folded Normal Distribution