Geometric transformation
In mathematics, a geometric transformation is any bijection of a set to itself (or to another such set) with some salient geometrical underpinning. More specifically, it is a function whose domain and range are sets of points — most often both [math]\displaystyle{ \mathbb{R}^2 }[/math] or both [math]\displaystyle{ \mathbb{R}^3 }[/math] — such that the function is bijective so that its inverse exists.[1] The study of geometry may be approached by the study of these transformations.[2]
Classifications
Geometric transformations can be classified by the dimension of their operand sets (thus distinguishing between, say, planar transformations and spatial transformations). They can also be classified according to the properties they preserve:
- Displacements preserve distances and oriented angles (e.g., translations);[3]
- Isometries preserve angles and distances (e.g., Euclidean transformations);[4][5]
- Similarities preserve angles and ratios between distances (e.g., resizing);[6]
- Affine transformations preserve parallelism (e.g., scaling, shear);[5][7]
- Projective transformations preserve collinearity;[8]
Each of these classes contains the previous one.[8]
- Möbius transformations using complex coordinates on the plane (as well as circle inversion) preserve the set of all lines and circles, but may interchange lines and circles.
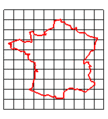
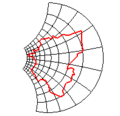
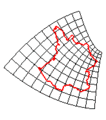
Original image (based on the map of France)
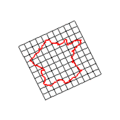
Inversion
.gif)
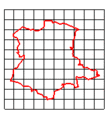
- Conformal transformations preserve angles, and are, in the first order, similarities.
- Equiareal transformations, preserve areas in the planar case or volumes in the three dimensional case.[9] and are, in the first order, affine transformations of determinant 1.
- Homeomorphisms (bicontinuous transformations) preserve the neighborhoods of points.
- Diffeomorphisms (bidifferentiable transformations) are the transformations that are affine in the first order; they contain the preceding ones as special cases, and can be further refined.
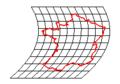
Conformal transformation
Transformations of the same type form groups that may be sub-groups of other transformation groups.
Opposite group actions
Many geometric transformations are expressed with linear algebra. The bijective linear transformations are elements of a general linear group. The linear transformation A is non-singular. For a row vector v, the matrix product vA gives another row vector w = vA.
The transpose of a row vector v is a column vector vT, and the transpose of the above equality is [math]\displaystyle{ w^T = (vA)^T = A^T v^T . }[/math] Here AT provides a left action on column vectors.
In transformation geometry there are compositions AB. Starting with a row vector v, the right action of the composed transformation is w = vAB. After transposition,
- [math]\displaystyle{ w^T = (vAB)^T = (AB)^Tv^T = B^T A^T v^T . }[/math]
Thus for AB the associated left group action is [math]\displaystyle{ B^T A^T . }[/math] In the study of opposite groups, the distinction is made between opposite group actions because commutative groups are the only groups for which these opposites are equal.
See also
- Coordinate transformation
- Erlangen program
- Symmetry (geometry)
- Motion
- Reflection
- Rigid transformation
- Rotation
- Topology
- Transformation matrix
References
- ↑ Usiskin, Zalman; Peressini, Anthony L.; Marchisotto, Elena; Stanley, Dick (2003). Mathematics for High School Teachers: An Advanced Perspective. Pearson Education. p. 84. ISBN 0-13-044941-5. OCLC 50004269.
- ↑ Venema, Gerard A. (2006), Foundations of Geometry, Pearson Prentice Hall, p. 285, ISBN 9780131437005
- ↑ "Geometry Translation". https://www.mathsisfun.com/geometry/translation.html.
- ↑ "Geometric Transformations — Euclidean Transformations". https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/geometry/geo-tran.html#euclidean.
- ↑ 5.0 5.1 Geometric transformation, p. 131, at Google Books
- ↑ "Transformations". https://www.mathsisfun.com/geometry/transformations.html.
- ↑ "Geometric Transformations — Affine Transformations". https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/geometry/geo-tran.html#affine.
- ↑ 8.0 8.1 Leland Wilkinson, D. Wills, D. Rope, A. Norton, R. Dubbs – 'Geometric transformation, p. 182, at Google Books
- ↑ Geometric transformation, p. 191, at Google Books Bruce E. Meserve – Fundamental Concepts of Geometry, page 191.]
Further reading
- Adler, Irving (2012), A New Look at Geometry, Dover, ISBN 978-0-486-49851-5
- Dienes, Z. P.; Golding, E. W. (1967) . Geometry Through Transformations (3 vols.): Geometry of Distortion, Geometry of Congruence, and Groups and Coordinates. New York: Herder and Herder.
- David Gans – Transformations and geometries.
- Geometry and the Imagination (2nd ed.). Chelsea. 1952. ISBN 0-8284-1087-9.
- John McCleary (2013) Geometry from a Differentiable Viewpoint, Cambridge University Press ISBN:978-0-521-11607-7
- Modenov, P. S.; Parkhomenko, A. S. (1965) . Geometric Transformations (2 vols.): Euclidean and Affine Transformations, and Projective Transformations. New York: Academic Press.
- A. N. Pressley – Elementary Differential Geometry.
- Yaglom, I. M. (1962, 1968, 1973, 2009) . Geometric Transformations (4 vols.). Random House (I, II & III), MAA (I, II, III & IV).
 |  |
