Gustafson's law
In computer architecture, Gustafson's law (or Gustafson–Barsis's law[1]) gives the speedup in the execution time of a task that theoretically gains from parallel computing, using a hypothetical run of the task on a single-core machine as the baseline. To put it another way, it is the theoretical "slowdown" of an already parallelized task if running on a serial machine. It is named after computer scientist John L. Gustafson and his colleague Edwin H. Barsis, and was presented in the article Reevaluating Amdahl's Law in 1988.[2]
Definition
Gustafson estimated the speedup [math]\displaystyle{ S }[/math] of a program gained by using parallel computing as follows:
[math]\displaystyle{ \begin{align} S &= s + p \times N \\ &= s + (1 - s) \times N \\ &= N + (1 - N) \times s \end{align} }[/math]
where
- [math]\displaystyle{ S }[/math] is the theoretical speedup of the program with parallelism (scaled speedup[2]);
- [math]\displaystyle{ N }[/math] is the number of processors;
- [math]\displaystyle{ s }[/math] and [math]\displaystyle{ p }[/math] are the fractions of time spent executing the serial parts and the parallel parts of the program on the parallel system, where [math]\displaystyle{ s + p = 1 }[/math].
Alternatively, [math]\displaystyle{ S }[/math] can be expressed using [math]\displaystyle{ p }[/math]:
[math]\displaystyle{ \begin{align} S &= (1 - p) + p \times N \\ &= 1 + (N - 1) \times p \end{align} }[/math]
Gustafson's law addresses the shortcomings of Amdahl's law, which is based on the assumption of a fixed problem size, that is of an execution workload that does not change with respect to the improvement of the resources. Gustafson's law instead proposes that programmers tend to increase the size of problems to fully exploit the computing power that becomes available as the resources improve.[2]
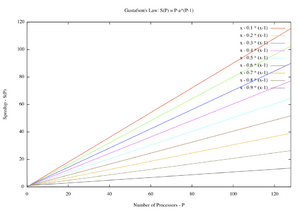
Gustafson and his colleagues further observed from their workloads that time for the serial part typically does not grow as the problem and the system scale,[2] that is, [math]\displaystyle{ s }[/math] is fixed. This gives a linear model between the processor count [math]\displaystyle{ N }[/math] and the speedup [math]\displaystyle{ S }[/math] with slope [math]\displaystyle{ 1 - s }[/math], as shown in the figure above (which uses different notations: [math]\displaystyle{ P }[/math] for [math]\displaystyle{ N }[/math] and [math]\displaystyle{ a }[/math] for [math]\displaystyle{ s }[/math]). Also, [math]\displaystyle{ S }[/math] scales linearly with [math]\displaystyle{ s }[/math] rather than exponentially in the Amdahl's Law.[2] With these observations, Gustafson "expect[ed] to extend [their] success [on parallel computing] to a broader range of applications and even larger values for [math]\displaystyle{ N }[/math]".[2]
The impact of Gustafson's law was to shift[citation needed] research goals to select or reformulate problems so that solving a larger problem in the same amount of time would be possible. In a way the law redefines efficiency, due to the possibility that limitations imposed by the sequential part of a program may be countered by increasing the total amount of computation.
Derivation
The execution time of a program running on a parallel system can be split into two parts:
- a part that does not benefit from the increasing number of processors (serial part);
- a part that benefits from the increasing number of processors (parallel part).
Example. — A computer program that processes files from disk. A part of that program may scan the directory of the disk and create a list of files internally in memory. After that, another part of the program passes each file to a separate thread for processing. The part that scans the directory and creates the file list cannot be sped up on a parallel computer, but the part that processes the files can.
Without loss of generality, let the total execution time on the parallel system be [math]\displaystyle{ T = 1 }[/math]. Denote the serial time as [math]\displaystyle{ s }[/math] and the parallel time as [math]\displaystyle{ p }[/math], where [math]\displaystyle{ s + p = 1 }[/math]. Denote the number of processors as [math]\displaystyle{ N }[/math].
Hypothetically, when running the program on a serial system (only one processor), the serial part still takes [math]\displaystyle{ s }[/math], while the parallel part now takes [math]\displaystyle{ Np }[/math]. The execution time on the serial system is:
[math]\displaystyle{ T' = s + Np }[/math] Using [math]\displaystyle{ T' }[/math] as the baseline, the speedup for the parallel system is:
[math]\displaystyle{ S = \frac{T'}{T} = \frac{s + Np}{s + p} = \frac{s + Np}{1} = s + Np }[/math]
By substituting [math]\displaystyle{ p = 1 - s }[/math] or [math]\displaystyle{ s = 1 - p }[/math], several forms in the previous section can be derived.
Applications
Application in research
Amdahl's law presupposes that the computing requirements will stay the same, given increased processing power. In other words, an analysis of the same data will take less time given more computing power.
Gustafson, on the other hand, argues that more computing power will cause the data to be more carefully and fully analyzed: pixel by pixel or unit by unit, rather than on a larger scale. Where it would not have been possible or practical to simulate the impact of nuclear detonation on every building, car, and their contents (including furniture, structure strength, etc.) because such a calculation would have taken more time than was available to provide an answer, the increase in computing power will prompt researchers to add more data to more fully simulate more variables, giving a more accurate result.
Application in everyday computer systems
Amdahl's Law reveals a limitation in, for example, the ability of multiple cores to reduce the time it takes for a computer to boot to its operating system and be ready for use. Assuming the boot process was mostly parallel, quadrupling computing power on a system that took one minute to load might reduce the boot time to just over fifteen seconds. But greater and greater parallelization would eventually fail to make bootup go any faster, if any part of the boot process were inherently sequential.
Gustafson's law argues that a fourfold increase in computing power would instead lead to a similar increase in expectations of what the system will be capable of. If the one-minute load time is acceptable to most users, then that is a starting point from which to increase the features and functions of the system. The time taken to boot to the operating system will be the same, i.e. one minute, but the new system would include more graphical or user-friendly features.
Limitations
Some problems do not have fundamentally larger datasets. As an example, processing one data point per world citizen gets larger at only a few percent per year. The principal point of Gustafson's law is that such problems are not likely to be the most fruitful applications of parallelism.
Algorithms with nonlinear runtimes may find it hard to take advantage of parallelism "exposed" by Gustafson's law. Snyder[3] points out an [math]\displaystyle{ O(N^3) }[/math] algorithm means that double the concurrency gives only about a 26% increase in problem size. Thus, while it may be possible to occupy vast concurrency, doing so may bring little advantage over the original, less concurrent solution—however in practice there have still been considerable improvements.
Hill and Marty[4] emphasize also that methods of speeding sequential execution are still needed, even for multicore machines. They point out that locally inefficient methods can be globally efficient when they reduce the sequential phase. Furthermore, Woo and Lee[5] studied the implication of energy and power on future many-core processors based on Amdahl's law, showing that an asymmetric many-core processor can achieve the best possible energy efficiency by activating an optimal number of cores given the amount of parallelism is known prior to execution.
Al-hayanni, Rafiev et al have developed novel speedup and energy consumption models based on a general representation of core heterogeneity, referred to as the normal form heterogeneity, that support a wide range of heterogeneous many-core architectures. These modelling methods aim to predict system power efficiency and performance ranges, and facilitates research and development at the hardware and system software levels.[6][7]
See also
References
- ↑ McCool, Michael D.; Robison, Arch D.; Reinders, James (2012). "2.5 Performance Theory". Structured Parallel Programming: Patterns for Efficient Computation. Elsevier. pp. 61–62. ISBN 978-0-12-415993-8. https://books.google.com/books?id=zpaHa5cjLwwC&pg=PA61.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 Gustafson, John L. (May 1988). "Reevaluating Amdahl's Law". Communications of the ACM 31 (5): 532–3. doi:10.1145/42411.42415. http://www.johngustafson.net/pubs/pub13/amdahl.htm.
- ↑ Snyder, Lawrence (June 1986). "Type Architectures, Shared Memory, and The Corollary of Modest Potential". Annu. Rev. Comput. Sci. 1: 289–317. doi:10.1146/annurev.cs.01.060186.001445. http://www.cs.washington.edu/homes/snyder/TypeArchitectures.pdf.
- ↑ Hill, Mark D.; Marty, Michael R. (July 2008). "Amdahl's Law in the Multicore Era". IEEE Computer 41 (7): 33–38. doi:10.1109/MC.2008.209. UW CS-TR-2007-1593. http://www.cs.wisc.edu/multifacet/amdahl/.
- ↑ Dong Hyuk Woo; Hsien-Hsin S. Lee (December 2008). "Extending Amdahl's Law for Energy-Efficient Computing in the Many-Core Era". IEEE Computer 41 (12): 24–31. doi:10.1109/mc.2008.494.
- ↑ Rafiev, Ashur; Al-Hayanni, Mohammed A. N.; Xia, Fei; Shafik, Rishad; Romanovsky, Alexander; Yakovlev, Alex (2018-07-01). "Speedup and Power Scaling Models for Heterogeneous Many-Core Systems". IEEE Transactions on Multi-Scale Computing Systems 4 (3): 436–449. doi:10.1109/TMSCS.2018.2791531. ISSN 2332-7766. https://eprint.ncl.ac.uk/fulltext.aspx?url=245030/F5112E01-B564-454E-BC28-B648451B48FE.pdf&pub_id=245030.
- ↑ Al-hayanni, Mohammed A. Noaman; Xia, Fei; Rafiev, Ashur; Romanovsky, Alexander; Shafik, Rishad; Yakovlev, Alex (July 2020). "Amdahl's law in the context of heterogeneous many-core systems – a survey" (in en). IET Computers & Digital Techniques 14 (4): 133–148. doi:10.1049/iet-cdt.2018.5220. ISSN 1751-8601.
 |