Evil number

Short description: Class of binary number

evil	odious
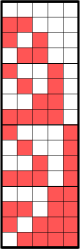
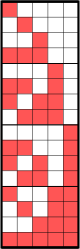
The first 16 evil and odious numbers in little-endian binary. It can be seen, that both sequences differ only in the least significant bits, which form the Thue–Morse sequence for the evil, and its negation for the odious numbers. The other bits form the even numbers.

In number theory, an evil number is a non-negative integer that has an even number of 1s in its binary expansion. These numbers give the positions of the zero values in the Thue–Morse sequence, and for this reason they have also been called the Thue–Morse set. Non-negative integers that are not evil are called odious numbers.

Examples

The first evil numbers are:

0, 3, 5, 6, 9, 10, 12, 15, 17, 18, 20, 23, 24, 27, 29, 30, 33, 34, 36, 39 ...

Equal sums

The partition of the non-negative integers into the odious and evil numbers is the unique partition of these numbers into two sets that have equal multisets of pairwise sums.

As 19th-century mathematician Eugène Prouhet showed, the partition into evil and odious numbers of the numbers from [math]\displaystyle{ 0 }[/math] to [math]\displaystyle{ 2^k-1 }[/math], for any [math]\displaystyle{ k }[/math], provides a solution to the Prouhet–Tarry–Escott problem of finding sets of numbers whose sums of powers are equal up to the [math]\displaystyle{ k }[/math]th power.

In computer science

In computer science, an evil number is said to have even parity.