Holomorphic functional calculus
In mathematics, holomorphic functional calculus is functional calculus with holomorphic functions. That is to say, given a holomorphic function f of a complex argument z and an operator T, the aim is to construct an operator, f(T), which naturally extends the function f from complex argument to operator argument. More precisely, the functional calculus defines a continuous algebra homomorphism from the holomorphic functions on a neighbourhood of the spectrum of T to the bounded operators.
This article will discuss the case where T is a bounded linear operator on some Banach space. In particular, T can be a square matrix with complex entries, a case which will be used to illustrate functional calculus and provide some heuristic insights for the assumptions involved in the general construction.
Motivation
Need for a general functional calculus
In this section T will be assumed to be a n × n matrix with complex entries.
If a given function f is of certain special type, there are natural ways of defining f(T). For instance, if
is a complex polynomial, one can simply substitute T for z and define
where T0 = I, the identity matrix. This is the polynomial functional calculus. It is a homomorphism from the ring of polynomials to the ring of n × n matrices.
Extending slightly from the polynomials, if f : C → C is holomorphic everywhere, i.e. an entire function, with MacLaurin series
mimicking the polynomial case suggests we define
Since the MacLaurin series converges everywhere, the above series will converge, in a chosen operator norm. An example of this is the exponential of a matrix. Replacing z by T in the MacLaurin series of f(z) = ez gives
The requirement that the MacLaurin series of f converges everywhere can be relaxed somewhat. From above it is evident that all that is really needed is the radius of convergence of the MacLaurin series be greater than ǁTǁ, the operator norm of T. This enlarges somewhat the family of f for which f(T) can be defined using the above approach. However it is not quite satisfactory. For instance, it is a fact from matrix theory that every non-singular T has a logarithm S in the sense that eS = T. It is desirable to have a functional calculus that allows one to define, for a non-singular T, ln(T) such that it coincides with S. This can not be done via power series, for example the logarithmic series
converges only on the open unit disk. Substituting T for z in the series fails to give a well-defined expression for ln(T + I) for invertible T + I with ǁTǁ ≥ 1. Thus a more general functional calculus is needed.
Functional calculus and the spectrum
It is expected that a necessary condition for f(T) to make sense is f be defined on the spectrum of T. For example, the spectral theorem for normal matrices states every normal matrix is unitarily diagonalizable. This leads to a definition of f(T) when T is normal. One encounters difficulties if f(λ) is not defined for some eigenvalue λ of T.
Other indications also reinforce the idea that f(T) can be defined only if f is defined on the spectrum of T. If T is not invertible, then (recalling that T is an n x n matrix) 0 is an eigenvalue. Since the natural logarithm is undefined at 0, one would expect that ln(T) can not be defined naturally. This is indeed the case. As another example, for
the reasonable way of calculating f(T) would seem to be
However, this expression is not defined if the inverses on the right-hand side do not exist, that is, if either 2 or 5 are eigenvalues of T.
For a given matrix T, the eigenvalues of T dictate to what extent f(T) can be defined; i.e., f(λ) must be defined for all eigenvalues λ of T. For a general bounded operator this condition translates to "f must be defined on the spectrum of T". This assumption turns out to be an enabling condition such that the functional calculus map, f → f(T), has certain desirable properties.
Functional calculus for a bounded operator
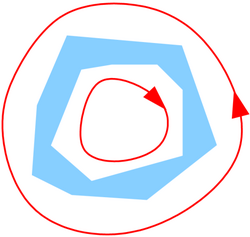
Let X be a complex Banach space, and L(X) denote the family of bounded operators on X.
Recall the Cauchy integral formula from classical function theory. Let f : C → C be holomorphic on some open set D ⊂ C, and Γ be a rectifiable Jordan curve in D, that is, a closed curve of finite length without self-intersections. Assume that the set U of points lying in the inside of Γ, i.e. such that the winding number of Γ about z is 1, is contained in D. The Cauchy integral formula states
for any z in U.
The idea is to extend this formula to functions taking values in the Banach space L(X). Cauchy's integral formula suggests the following definition (purely formal, for now):
where (ζ−T)−1 is the resolvent of T at ζ.
Assuming this Banach space-valued integral is appropriately defined, this proposed functional calculus implies the following necessary conditions:
- As the scalar version of Cauchy's integral formula applies to holomorphic f, we anticipate that is also the case for the Banach space case, where there should be a suitable notion of holomorphy for functions taking values in the Banach space L(X).
- As the resolvent mapping ζ → (ζ−T)−1 is undefined on the spectrum of T, σ(T), the Jordan curve Γ should not intersect σ(T). Now, the resolvent mapping will be holomorphic on the complement of σ(T). So to obtain a non-trivial functional calculus, Γ must enclose (at least part of) σ(T).
- The functional calculus should be well-defined in the sense that f(T) has to be independent of Γ.
The full definition of the functional calculus is as follows: For T ∈ L(X), define
where f is a holomorphic function defined on an open set D ⊂ C which contains σ(T), and Γ = {γ1, ..., γm} is a collection of disjoint Jordan curves in D bounding an "inside" set U, such that σ(T) lies in U, and each γi is oriented in the boundary sense.
The open set D may vary with f and need not be connected or simply connected, as shown by the figures on the right.
The following subsections make precise the notions invoked in the definition and show f(T) is indeed well defined under given assumptions.
Banach space-valued integral
- Cf. Bochner integral
For a continuous function g defined in an open neighborhood of Γ and taking values in L(X), the contour integral ∫Γg is defined in the same way as for the scalar case. One can parametrize each γi ∈ Γ by a real interval [a, b], and the integral is the limit of the Riemann sums obtained from ever-finer partitions of [a, b]. The Riemann sums converge in the uniform operator topology. We define
In the definition of the functional calculus, f is assumed to be holomorphic in an open neighborhood of Γ. It will be shown below that the resolvent mapping is holomorphic on the resolvent set. Therefore, the integral
makes sense.
The resolvent mapping
The mapping ζ → (ζ−T)−1 is called the resolvent mapping of T. It is defined on the complement of σ(T), called the resolvent set of T and will be denoted by ρ(T).
Much of classical function theory depends on the properties of the integral
The holomorphic functional calculus is similar in that the resolvent mapping plays a crucial role in obtaining properties one requires from a nice functional calculus. This subsection outlines properties of the resolvent map that are essential in this context.
The 1st resolvent formula
Direct calculation shows, for z1, z2 ∈ ρ(T),
Therefore,
This equation is called the first resolvent formula. The formula shows (z1−T)−1 and (z2−T)−1 commute, which hints at the fact that the image of the functional calculus will be a commutative algebra. Letting z2 → z1 shows the resolvent map is (complex-) differentiable at each z1 ∈ ρ(T); so the integral in the expression of functional calculus converges in L(X).
Analyticity
Stronger statement than differentiability can be made regarding the resolvent map. The resolvent set ρ(T) is actually an open set on which the resolvent map is analytic. This property will be used in subsequent arguments for the functional calculus. To verify this claim, let z1 ∈ ρ(T) and notice the formal expression
suggests we consider
for (z2−T)−1. The above series converges in L(X), which implies the existence of (z2−T)−1, if
Therefore, the resolvent set ρ(T) is open and the power series expression on an open disk centered at z1 ∈ ρ(T) shows the resolvent map is analytic on ρ(T).
Neumann series
Another expression for (z−T)−1 will also be useful. The formal expression
leads one to consider
This series, the Neumann series, converges to (z−T)−1 if
Compactness of σ(T)
From the last two properties of the resolvent we can deduce that the spectrum σ(T) of a bounded operator T is a compact subset of C. Therefore, for any open set D such that σ(T) ⊂ D, there exists a positively oriented and smooth system of Jordan curves Γ = {γ1, ..., γm} such that σ(T) is in the inside of Γ and the complement of D is contained in the outside of Γ. Hence, for the definition of the functional calculus, indeed a suitable family of Jordan curves can be found for each f that is holomorphic on some D.
Well-definedness
The previous discussion has shown that the integral makes sense, i.e. a suitable collection Γ of Jordan curves does exist for each f and the integral does converge in the appropriate sense. What has not been shown is that the definition of the functional calculus is unambiguous, i.e. does not depend on the choice of Γ. This issue we now try to resolve.
A preliminary fact
For a collection of Jordan curves Γ = {γ1, ..., γm} and a point a ∈ C, the winding number of Γ with respect to a is the sum of the winding numbers of its elements. If we define:
the following theorem is by Cauchy:
Theorem. Let G ⊂ C be an open set and Γ ⊂ G. If g : G → C is holomorphic, and for all a in the complement of G, n(Γ, a) = 0, then the contour integral of g on Γ is zero.
We will need the vector-valued analog of this result when g takes values in L(X). To this end, let g : G → L(X) be holomorphic, with the same assumptions on Γ. The idea is use the dual space L(X)* of L(X), and pass to Cauchy's theorem for the scalar case.
Consider the integral
if we can show that all φ ∈ L(X)* vanish on this integral then the integral itself has to be zero. Since φ is bounded and the integral converges in norm, we have:
But g is holomorphic, hence the composition φ(g): G ⊂ C → C is holomorphic and therefore by Cauchy's theorem
Main argument
The well-definedness of functional calculus now follows as an easy consequence. Let D be an open set containing σ(T). Suppose Γ = {γi} and Ω = {ωj} are two (finite) collections of Jordan curves satisfying the assumption given for the functional calculus. We wish to show
Let Ω′ be obtained from Ω by reversing the orientation of each ωj, then
Consider the union of the two collections Γ ∪ Ω′. Both Γ ∪ Ω′ and σ(T) are compact. So there is some open set U containing Γ ∪ Ω′ such that σ(T) lies in the complement of U. Any a in the complement of U has winding number n(Γ ∪ Ω′, a) = 0[clarification needed] and the function
is holomorphic on U. So the vector-valued version of Cauchy's theorem gives
i.e.
Hence the functional calculus is well-defined.
Consequently, if f1 and f2 are two holomorphic functions defined on neighborhoods D1 and D2 of σ(T) and they are equal on an open set containing σ(T), then f1(T) = f2(T). Moreover, even though the D1 may not be D2, the operator (f1 + f2) (T) is well-defined. Same holds for the definition of (f1·f2)(T).
On the assumption that f be holomorphic over an open neighborhood of σ(T)
So far the full strength of this assumption has not been used. For convergence of the integral, only continuity was used. For well-definedness, we only needed f to be holomorphic on an open set U containing the contours Γ ∪ Ω′ but not necessarily σ(T). The assumption will be applied in its entirety in showing the homomorphism property of the functional calculus.
Properties
Polynomial case
The linearity of the map f ↦ f(T) follows from the convergence of the integral and that linear operations on a Banach space are continuous.
We recover the polynomial functional calculus when f(z) = Σ0 ≤ i ≤ m ai zi is a polynomial. To prove this, it is sufficient to show, for k ≥ 0 and f(z) = zk, it is true that f(T) = Tk, i.e.
for any suitable Γ enclosing σ(T). Choose Γ to be a circle of radius greater than the operator norm of T. As stated above, on such Γ, the resolvent map admits a power series representation
Substituting gives
which is
The δ is the Kronecker delta symbol.
The homomorphism property
For any f1 and f2 satisfying the appropriate assumptions, the homomorphism property states
We sketch an argument which invokes the first resolvent formula and the assumptions placed on f. First we choose the Jordan curves such that Γ1 lies in the inside of Γ2. The reason for this will become clear below. Start by calculating directly
The last line follows from the fact that ω ∈ Γ2 lies outside of Γ1 and f1 is holomorphic on some open neighborhood of σ(T) and therefore the second term vanishes. Therefore, we have:
Continuity with respect to compact convergence
Let G ⊂ C be open with σ(T) ⊂ G. Suppose a sequence {fk} of holomorphic functions on G converges uniformly on compact subsets of G (this is sometimes called compact convergence). Then {fk(T)} is convergent in L(X):
Assume for simplicity that Γ consists of only one Jordan curve. We estimate
By combining the uniform convergence assumption and various continuity considerations, we see that the above tends to 0 as k, l → ∞. So {fk(T)} is Cauchy, therefore convergent.
Uniqueness
To summarize, we have shown the holomorphic functional calculus, f → f(T), has the following properties:
- It extends the polynomial functional calculus.
- It is an algebra homomorphism from the algebra of holomorphic functions defined on a neighborhood of σ(T) to L(X)
- It preserves uniform convergence on compact sets.
It can be proved that a calculus satisfying the above properties is unique.
We note that, everything discussed so far holds verbatim if the family of bounded operators L(X) is replaced by a Banach algebra A. The functional calculus can be defined in exactly the same way for an element in A.
Spectral considerations
Spectral mapping theorem
It is known that the spectral mapping theorem holds for the polynomial functional calculus: for any polynomial p, σ(p(T)) = p(σ(T)). This can be extended to the holomorphic calculus. To show f(σ(T)) ⊂ σ(f(T)), let μ be any complex number. By a result from complex analysis, there exists a function g holomorphic on a neighborhood of σ(T) such that
According to the homomorphism property, f(T) − f(μ) = (T − μ)g(T). Therefore, μ ∈ σ(T) implies f(μ) ∈ σ(f(T)).
For the other inclusion, if μ is not in f(σ(T)), then the functional calculus is applicable to
So g(T)(f(T) − μ) = I. Therefore, μ does not lie in σ(f(T)).
Spectral projections
The underlying idea is as follows. Suppose that K is a subset of σ(T) and U,V are disjoint neighbourhoods of K and σ(T) \ K respectively. Define e(z) = 1 if z ∈ U and e(z) = 0 if z ∈ V. Then e is a holomorphic function with [e(z)]2 = e(z) and so, for a suitable contour Γ which lies in U ∪ V and which encloses σ(T), the linear operator
will be a bounded projection that commutes with T and provides a great deal of useful information.
It transpires that this scenario is possible if and only if K is both open and closed in the subspace topology on σ(T). Moreover, the set V can be safely ignored since e is zero on it and therefore makes no contribution to the integral. The projection e(T) is called the spectral projection of T at K and is denoted by P(K;T). Thus every subset K of σ(T) that is both open and closed in the subspace topology has an associated spectral projection given by
where Γ is a contour that encloses K but no other points of σ(T).
Since P = P(K;T) is bounded and commutes with T it enables T to be expressed in the form U ⊕ V where U = T|PX and V = T|(1−P)X. Both PX and (1 − P)X are invariant subspaces of T moreover σ(U) = K and σ(V) = σ(T) \ K. A key property is mutual orthogonality. If L is another open and closed set in the subspace topology on σ(T) then P(K;T)P(L;T) = P(L;T)P(K;T) = P(K ∩ L;T) which is zero whenever K and L are disjoint.
Spectral projections have numerous applications. Any isolated point of σ(T) is both open and closed in the subspace topology and therefore has an associated spectral projection. When X has finite dimension σ(T) consists of isolated points and the resultant spectral projections lead to a variant of Jordan normal form wherein all the Jordan blocks corresponding to the same eigenvalue are consolidated. In other words there is precisely one block per distinct eigenvalue. The next section considers this decomposition in more detail.
Sometimes spectral projections inherit properties from their parent operators. For example if T is a positive matrix with spectral radius r then the Perron–Frobenius theorem asserts that r ∈ σ(T). The associated spectral projection P = P(r;T) is also positive and by mutual orthogonality no other spectral projection can have a positive row or column. In fact TP = rP and (T/r)n → P as n → ∞ so this projection P (which is called the Perron projection) approximates (T/r)n as n increases, and each of its columns is an eigenvector of T.
More generally if T is a compact operator then all non-zero points in σ(T) are isolated and so any finite subset of them can be used to decompose T. The associated spectral projection always has finite rank. Those operators in L(X) with similar spectral characteristics are known as Riesz operators. Many classes of Riesz operators (including the compact operators) are ideals in L(X) and provide a rich field for research. However if X is a Hilbert space there is exactly one closed ideal sandwiched between the Riesz operators and those of finite rank.
Much of the foregoing discussion can be set in the more general context of a complex Banach algebra. Here spectral projections are referred to as spectral idempotents since there may no longer be a space for them to project onto.
Invariant subspace decomposition
If the spectrum σ(T) is not connected, X can be decomposed into invariant subspaces of T using the functional calculus. Let σ(T) be a disjoint union
Define ei to be 1 on some neighborhood that contains only the component Fi and 0 elsewhere. By the homomorphism property, ei(T) is a projection for all i. In fact it is just the spectral projection P(Fi;T) described above. The relation ei(T) T = T ei(T) means the range of each ei(T), denoted by Xi, is an invariant subspace of T. Since
X can be expressed in terms of these complementary subspaces:
Similarly, if Ti is T restricted to Xi, then
Consider the direct sum
With the norm
X' is a Banach space. The mapping R: X' → X defined by
is a Banach space isomorphism, and we see that
This can be viewed as a block diagonalization of T.
When X is finite-dimensional, σ(T) = {λi} is a finite set of points in the complex plane. Choose ei to be 1 on an open disc containing only λi from the spectrum. The corresponding block-diagonal matrix
is the Jordan canonical form of T.
Related results
With stronger assumptions, when T is a normal operator acting on a Hilbert space, the domain of the functional calculus can be broadened. When comparing the two results, a rough analogy can be made with the relationship between the spectral theorem for normal matrices and the Jordan canonical form. When T is a normal operator, a continuous functional calculus can be obtained, that is, one can evaluate f(T) with f being a continuous function defined on σ(T). Using the machinery of measure theory, this can be extended to functions which are only measurable (see Borel functional calculus). In that context, if E ⊂ σ(T) is a Borel set and 1E is the characteristic function of E, the projection operator 1E(T) is a refinement of ei(T) discussed above.
The Borel functional calculus extends to unbounded self-adjoint operators on a Hilbert space.
In slightly more abstract language, the holomorphic functional calculus can be extended to any element of a Banach algebra, using essentially the same arguments as above. Similarly, the continuous functional calculus holds for normal elements in any C*-algebra and the measurable functional calculus for normal elements in any von Neumann algebra.
Unbounded operators
A holomorphic functional calculus can be defined in a similar fashion for unbounded closed operators with non-empty resolvent set.
See also
- Resolvent formalism
- Jordan canonical form, where the finite-dimensional case is discussed in some detail.
References
- N. Dunford and J.T. Schwartz, Linear Operators, Part I: General Theory, Interscience, 1958.
- Steven G Krantz. Dictionary of Algebra, Arithmetic, and Trigonometry. CRC Press, 2000. ISBN 1-58488-052-X.
- Israel Gohberg, Seymour Goldberg and Marinus A. Kaashoek, Classes of Linear Operators: Volume 1. Birkhauser, 1991. ISBN 978-0817625313.
 |
