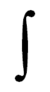Integral symbol

Short description: Mathematical symbol used to denote integrals and antiderivatives

∫
Integral symbol
In Unicode	U+222B ∫ INTEGRAL (HTML ∫ · ∫)
Graphical variants
[math]\displaystyle{ \displaystyle \int }[/math]
Different from
Different from	U+017F ſ LONG S U+0283 ʃ ESH

The integral symbol:

∫ (Unicode), [math]\displaystyle{ \displaystyle \int }[/math] (LaTeX)

is used to denote integrals and antiderivatives in mathematics, especially in calculus.

History

The notation was introduced by the Germany mathematician Gottfried Wilhelm Leibniz in 1675 in his private writings; it first appeared publicly in the article "De Geometria Recondita et analysi indivisibilium atque infinitorum" (On a hidden geometry and analysis of indivisibles and infinites), published in Acta Eruditorum in June 1686. The symbol was based on the ſ (long s) character and was chosen because Leibniz thought of the integral as an infinite sum of infinitesimal summands.

Typography in Unicode and LaTeX

Fundamental symbol

The integral symbol is U+222B ∫ INTEGRAL in Unicode and \int in LaTeX. In HTML, it is written as ∫ (hexadecimal), ∫ (decimal) and ∫ (named entity).

The original IBM PC code page 437 character set included a couple of characters ⌠ and ⌡ (codes 244 and 245 respectively) to build the integral symbol. These were deprecated in subsequent MS-DOS code pages, but they still remain in Unicode (U+2320 and U+2321 respectively) for compatibility.

The ∫ symbol is very similar to, but not to be confused with, the letter ʃ ("esh").

Extensions of the symbol

Related symbols include:

Meaning	Unicode		LaTeX
Double integral	∬	U+222C	[math]\displaystyle{ \iint }[/math]	\iint
Triple integral	∭	U+222D	[math]\displaystyle{ \iiint }[/math]	\iiint
Quadruple integral	⨌	U+2A0C	[math]\displaystyle{ \iiiint }[/math]	\iiiint
Contour integral	∮	U+222E	[math]\displaystyle{ \oint }[/math]	\oint
Clockwise integral	∱	U+2231
Counterclockwise integral	⨑	U+2A11
Clockwise contour integral	∲	U+2232	\varointclockwise
Counterclockwise contour integral	∳	U+2233	\ointctrclockwise
Closed surface integral	∯	U+222F		\oiint
Closed volume integral	∰	U+2230	\oiiint

Typography in other languages

Regional variations (English, German, and Russian from left to right) of the integral symbol

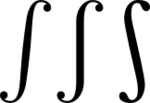
In other languages, the shape of the integral symbol differs slightly from the shape commonly seen in English-language textbooks. While the English integral symbol leans to the right, the German symbol (used throughout Central Europe) is upright, and the Russian variant leans slightly to the left to occupy less horizontal space.

Another difference is in the placement of limits for definite integrals. Generally, in English-language books, limits go to the right of the integral symbol:

[math]\displaystyle{ \int_0^5 f(t) \,\mathrm{d}t, \quad \int_{g(t) = a}^{g(t) = b} f(t) \,\mathrm{d}t. }[/math]

By contrast, in German and Russian texts, the limits are placed above and below the integral symbol, and, as a result, the notation requires larger line spacing but is more compact horizontally, especially when using longer expressions in the limits:

[math]\displaystyle{ \int\limits_0^T f(t) \,\mathrm{d}t, \quad \int\limits_{\!\!\!\!\!g(t) = a\!\!\!\!\!}^{\!\!\!\!\!g(t) = b\!\!\!\!\!} f(t) \,\mathrm{d}t. }[/math]

See also

• Capital sigma notation
• Capital pi notation

References

• Stewart, James (2003). "Integrals". Single Variable Calculus: Early Transcendentals (5th ed.). Belmont, CA: Brooks/Cole. p. 381. ISBN 0-534-39330-6. https://archive.org/details/singlevariableca00stew/page/381. 
• Zaitcev, V.; Janishewsky, A.; Berdnikov, A. (20 September 1999). "Russian Typographical Traditions in Mathematical Literature". EuroTeX'99. Heidelberg. https://www.staff.uni-giessen.de/~g029/eurotex99/zaitsev.pdf. 

External links

• Fileformat.info