Linear fractional transformation

Short description: Möbius transformation generalized to rings other than the complex numbers

In mathematics, a linear fractional transformation is, roughly speaking, an invertible transformation of the form

[math]\displaystyle{ z \mapsto \frac{az + b} {cz + d}. }[/math]

The precise definition depends on the nature of a, b, c, d, and z. In other words, a linear fractional transformation is a transformation that is represented by a fraction whose numerator and denominator are linear.

In the most basic setting, a, b, c, d, and z are complex numbers (in which case the transformation is also called a Möbius transformation), or more generally elements of a field. The invertibility condition is then ad – bc ≠ 0. Over a field, a linear fractional transformation is the restriction to the field of a projective transformation or homography of the projective line.

When a, b, c, d are integer (or, more generally, belong to an integral domain), z is supposed to be a rational number (or to belong to the field of fractions of the integral domain. In this case, the invertibility condition is that ad – bc must be a unit of the domain (that is 1 or −1 in the case of integers).

In the most general setting, the a, b, c, d and z are elements of a ring, such as square matrices. An example of such linear fractional transformation is the Cayley transform, which was originally defined on the 3 × 3 real matrix ring.

Linear fractional transformations are widely used in various areas of mathematics and its applications to engineering, such as classical geometry, number theory (they are used, for example, in Wiles's proof of Fermat's Last Theorem), group theory, control theory.

General definition

In general, a linear fractional transformation is a homography of P(A), the projective line over a ring A. When A is a commutative ring, then a linear fractional transformation has the familiar form

[math]\displaystyle{ z \mapsto \frac{az + b} {cz + d}, }[/math]

where a, b, c, d are elements of A such that ad – bc is a unit of A (that is ad – bc has a multiplicative inverse in A)

In a non-commutative ring A, with (z, t) in A², the units u determine an equivalence relation [math]\displaystyle{ (z,t) \sim (uz,ut) . }[/math] An equivalence class in the projective line over A is written U[z : t], where the brackets denote projective coordinates. Then linear fractional transformations act on the right of an element of P(A):

[math]\displaystyle{ U[z:t] \begin{pmatrix}a & c \\ b & d \end{pmatrix} = U[za + tb:\ zc + td] \sim U[(zc + td)^{-1}(za + tb):\ 1]. }[/math]

The ring is embedded in its projective line by z → U[z : 1], so t = 1 recovers the usual expression. This linear fractional transformation is well-defined since U[za + tb: zc + td] does not depend on which element is selected from its equivalence class for the operation.

The linear fractional transformations over A form a group, denoted [math]\displaystyle{ \operatorname{PGL}_1(A). }[/math]

The group [math]\displaystyle{ \operatorname{PGL}_1(\Z) }[/math] of the linear fractional transformations is called the modular group. It has been widely studied because of its numerous applications to number theory, which include, in particular, Wiles's proof of Fermat's Last Theorem.

Use in hyperbolic geometry

In the complex plane a generalized circle is either a line or a circle. When completed with the point at infinity, the generalized circles in the plane correspond to circles on the surface of the Riemann sphere, an expression of the complex projective line. Linear fractional transformations permute these circles on the sphere, and the corresponding finite points of the generalized circles in the complex plane.

To construct models of the hyperbolic plane the unit disk and the upper half-plane are used to represent the points. These subsets of the complex plane are provided a metric with the Cayley–Klein metric. Then the distance between two points is computed using the generalized circle through the points and perpendicular to the boundary of the subset used for the model. This generalized circle intersects the boundary at two other points. All four points are used in the cross ratio which defines the Cayley–Klein metric. Linear fractional transformations leave cross ratio invariant, so any linear fractional transformation that leaves the unit disk or upper half-planes stable is an isometry of the hyperbolic plane metric space. Since Henri Poincaré explicated these models they have been named after him: the Poincaré disk model and the Poincaré half-plane model. Each model has a group of isometries that is a subgroup of the Mobius group: the isometry group for the disk model is SU(1, 1) where the linear fractional transformations are "special unitary", and for the upper half-plane the isometry group is PSL(2, R), a projective linear group of linear fractional transformations with real entries and determinant equal to one.

Use in higher mathematics

Möbius transformations commonly appear in the theory of continued fractions, and in analytic number theory of elliptic curves and modular forms, as it describes the automorphisms of the upper half-plane under the action of the modular group. It also provides a canonical example of Hopf fibration, where the geodesic flow induced by the linear fractional transformation decomposes complex projective space into stable and unstable manifolds, with the horocycles appearing perpendicular to the geodesics. See Anosov flow for a worked example of the fibration: in this example, the geodesics are given by the fractional linear transform

[math]\displaystyle{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \cdot i\exp(t) = \frac{ai\exp(t)+b}{ci\exp(t)+d} , }[/math]

with a, b, c and d real, with ad − bc = 1. Roughly speaking, the center manifold is generated by the parabolic transformations, the unstable manifold by the hyperbolic transformations, and the stable manifold by the elliptic transformations.

Use in control theory

Linear fractional transformations are widely used in control theory to solve plant-controller relationship problems in mechanical and electrical engineering. The general procedure of combining linear fractional transformations with the Redheffer star product allows them to be applied to the scattering theory of general differential equations, including the S-matrix approach in quantum mechanics and quantum field theory, the scattering of acoustic waves in media (e.g. thermoclines and submarines in oceans, etc.) and the general analysis of scattering and bound states in differential equations. Here, the 3 × 3 matrix components refer to the incoming, bound and outgoing states. Perhaps the simplest example application of linear fractional transformations occurs in the analysis of the damped harmonic oscillator. Another elementary application is obtaining the Frobenius normal form, i.e. the companion matrix of a polynomial.

Conformal property

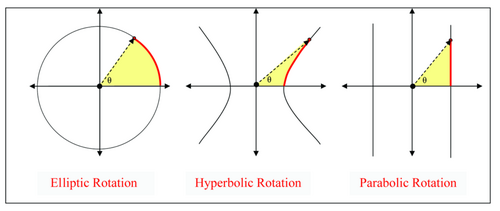
The commutative rings of split-complex numbers and dual numbers join the ordinary complex numbers as rings that express angle and "rotation". In each case the exponential map applied to the imaginary axis produces an isomorphism between one-parameter groups in (A, + ) and in the group of units (U, × ):

[math]\displaystyle{ \exp(y j) = \cosh y + j \sinh y, \quad j^2 = +1 , }[/math]

[math]\displaystyle{ \exp(y \epsilon) = 1 + y \epsilon, \quad \epsilon^2 = 0 , }[/math]

[math]\displaystyle{ \exp(y i) = \cos y + i \sin y, \quad i^2 = -1 . }[/math]

The "angle" y is hyperbolic angle, slope, or circular angle according to the host ring.

Linear fractional transformations are shown to be conformal maps by consideration of their generators: multiplicative inversion z → 1/z and affine transformations z → az + b. Conformality can be confirmed by showing the generators are all conformal. The translation z → z + b is a change of origin and makes no difference to angle. To see that z → az is conformal, consider the polar decomposition of a and z. In each case the angle of a is added to that of z resulting in a conformal map. Finally, inversion is conformal since z → 1/z sends [math]\displaystyle{ \exp(y b) \mapsto \exp(-y b), \quad b^2 = 1, 0, -1 . }[/math]

See also

• Laguerre transformations
• Linear-fractional programming
• H-infinity methods in control theory

References

• B.A. Dubrovin, A.T. Fomenko, S.P. Novikov (1984) Modern Geometry — Methods and Applications, volume 1, chapter 2, §15 Conformal transformations of Euclidean and Pseudo-Euclidean spaces of several dimensions, Springer-Verlag ISBN 0-387-90872-2.
• Geoffry Fox (1949) Elementary Theory of a hypercomplex variable and the theory of conformal mapping in the hyperbolic plane, Master's thesis, University of British Columbia.
• P.G. Gormley (1947) "Stereographic projection and the linear fractional group of transformations of quaternions", Proceedings of the Royal Irish Academy, Section A 51:67–85.
• A.E. Motter & M.A.F. Rosa (1998) "Hyperbolic calculus", Advances in Applied Clifford Algebras 8(1):109 to 28, §4 Conformal transformations, page 119.
• Tsurusaburo Takasu (1941) Gemeinsame Behandlungsweise der elliptischen konformen, hyperbolischen konformen und parabolischen konformen Differentialgeometrie, 2, Proceedings of the Imperial Academy 17(8): 330–8, link from Project Euclid, MR14282
• Isaak Yaglom (1968) Complex Numbers in Geometry, page 130 & 157, Academic Press