Restriction (mathematics)

Short description: Function with a smaller domain

The function [math]\displaystyle{ x^2 }[/math] with domain [math]\displaystyle{ \mathbb{R} }[/math] does not have an inverse function. If we restrict [math]\displaystyle{ x^2 }[/math] to the non-negative real numbers, then it does have an inverse function, known as the square root of [math]\displaystyle{ x. }[/math]

In mathematics, the restriction of a function [math]\displaystyle{ f }[/math] is a new function, denoted [math]\displaystyle{ f\vert_A }[/math] or [math]\displaystyle{ f {\restriction_A}, }[/math] obtained by choosing a smaller domain [math]\displaystyle{ A }[/math] for the original function [math]\displaystyle{ f. }[/math] The function [math]\displaystyle{ f }[/math] is then said to extend [math]\displaystyle{ f\vert_A. }[/math]

Formal definition

Let [math]\displaystyle{ f : E \to F }[/math] be a function from a set [math]\displaystyle{ E }[/math] to a set [math]\displaystyle{ F. }[/math] If a set [math]\displaystyle{ A }[/math] is a subset of [math]\displaystyle{ E, }[/math] then the restriction of [math]\displaystyle{ f }[/math] to [math]\displaystyle{ A }[/math] is the function [math]\displaystyle{ {f|}_A : A \to F }[/math] given by [math]\displaystyle{ {f|}_A(x) = f(x) }[/math] for [math]\displaystyle{ x \in A. }[/math] Informally, the restriction of [math]\displaystyle{ f }[/math] to [math]\displaystyle{ A }[/math] is the same function as [math]\displaystyle{ f, }[/math] but is only defined on [math]\displaystyle{ A }[/math].

If the function [math]\displaystyle{ f }[/math] is thought of as a relation [math]\displaystyle{ (x,f(x)) }[/math] on the Cartesian product [math]\displaystyle{ E \times F, }[/math] then the restriction of [math]\displaystyle{ f }[/math] to [math]\displaystyle{ A }[/math] can be represented by its graph,

[math]\displaystyle{ G({f|}_A) = \{ (x,f(x))\in G(f) : x\in A \} = G(f)\cap (A\times F), }[/math]

where the pairs [math]\displaystyle{ (x,f(x)) }[/math] represent ordered pairs in the graph [math]\displaystyle{ G. }[/math]

Extensions

A function [math]\displaystyle{ F }[/math] is said to be an extension of another function [math]\displaystyle{ f }[/math] if whenever [math]\displaystyle{ x }[/math] is in the domain of [math]\displaystyle{ f }[/math] then [math]\displaystyle{ x }[/math] is also in the domain of [math]\displaystyle{ F }[/math] and [math]\displaystyle{ f(x) = F(x). }[/math] That is, if [math]\displaystyle{ \operatorname{domain} f \subseteq \operatorname{domain} F }[/math] and [math]\displaystyle{ F\big\vert_{\operatorname{domain} f} = f. }[/math]

A linear extension (respectively, continuous extension, etc.) of a function [math]\displaystyle{ f }[/math] is an extension of [math]\displaystyle{ f }[/math] that is also a linear map (respectively, a continuous map, etc.).

Examples

1. The restriction of the non-injective function[math]\displaystyle{ f: \mathbb{R} \to \mathbb{R}, \ x \mapsto x^2 }[/math] to the domain [math]\displaystyle{ \mathbb{R}_{+} = [0,\infty) }[/math] is the injection[math]\displaystyle{ f:\mathbb{R}_+ \to \mathbb{R}, \ x \mapsto x^2. }[/math]
2. The factorial function is the restriction of the gamma function to the positive integers, with the argument shifted by one: [math]\displaystyle{ {\Gamma|}_{\mathbb{Z}^+}\!(n) = (n-1)! }[/math]

Properties of restrictions

• Restricting a function [math]\displaystyle{ f:X\rightarrow Y }[/math] to its entire domain [math]\displaystyle{ X }[/math] gives back the original function, that is, [math]\displaystyle{ f|_X = f. }[/math]
• Restricting a function twice is the same as restricting it once, that is, if [math]\displaystyle{ A \subseteq B \subseteq \operatorname{dom} f, }[/math] then [math]\displaystyle{ \left(f|_B\right)|_A = f|_A. }[/math]
• The restriction of the identity function on a set [math]\displaystyle{ X }[/math] to a subset [math]\displaystyle{ A }[/math] of [math]\displaystyle{ X }[/math] is just the inclusion map from [math]\displaystyle{ A }[/math] into [math]\displaystyle{ X. }[/math]
• The restriction of a continuous function is continuous.

Applications

Inverse functions

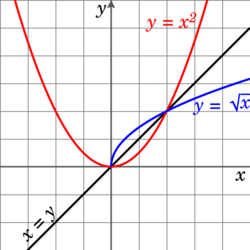
For a function to have an inverse, it must be one-to-one. If a function [math]\displaystyle{ f }[/math] is not one-to-one, it may be possible to define a partial inverse of [math]\displaystyle{ f }[/math] by restricting the domain. For example, the function [math]\displaystyle{ f(x) = x^2 }[/math] defined on the whole of [math]\displaystyle{ \R }[/math] is not one-to-one since [math]\displaystyle{ x^2 = (-x)^2 }[/math] for any [math]\displaystyle{ x \in \R. }[/math] However, the function becomes one-to-one if we restrict to the domain [math]\displaystyle{ \R_{\geq 0} = [0, \infty), }[/math] in which case [math]\displaystyle{ f^{-1}(y) = \sqrt{y} . }[/math]

(If we instead restrict to the domain [math]\displaystyle{ (-\infty, 0], }[/math] then the inverse is the negative of the square root of [math]\displaystyle{ y. }[/math]) Alternatively, there is no need to restrict the domain if we allow the inverse to be a multivalued function.

Selection operators

In relational algebra, a selection (sometimes called a restriction to avoid confusion with SQL's use of SELECT) is a unary operation written as [math]\displaystyle{ \sigma_{a \theta b}(R) }[/math] or [math]\displaystyle{ \sigma_{a \theta v}(R) }[/math] where:

• [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] are attribute names,
• [math]\displaystyle{ \theta }[/math] is a binary operation in the set [math]\displaystyle{ \{\lt , \leq, =, \neq, \geq, \gt \}, }[/math]
• [math]\displaystyle{ v }[/math] is a value constant,
• [math]\displaystyle{ R }[/math] is a relation.

The selection [math]\displaystyle{ \sigma_{a \theta b}(R) }[/math] selects all those tuples in [math]\displaystyle{ R }[/math] for which [math]\displaystyle{ \theta }[/math] holds between the [math]\displaystyle{ a }[/math] and the [math]\displaystyle{ b }[/math] attribute.

The selection [math]\displaystyle{ \sigma_{a \theta v}(R) }[/math] selects all those tuples in [math]\displaystyle{ R }[/math] for which [math]\displaystyle{ \theta }[/math] holds between the [math]\displaystyle{ a }[/math] attribute and the value [math]\displaystyle{ v. }[/math]

Thus, the selection operator restricts to a subset of the entire database.

The pasting lemma

The pasting lemma is a result in topology that relates the continuity of a function with the continuity of its restrictions to subsets.

Let [math]\displaystyle{ X,Y }[/math] be two closed subsets (or two open subsets) of a topological space [math]\displaystyle{ A }[/math] such that [math]\displaystyle{ A = X \cup Y, }[/math] and let [math]\displaystyle{ B }[/math] also be a topological space. If [math]\displaystyle{ f: A \to B }[/math] is continuous when restricted to both [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y, }[/math] then [math]\displaystyle{ f }[/math] is continuous.

This result allows one to take two continuous functions defined on closed (or open) subsets of a topological space and create a new one.

Sheaves

Sheaves provide a way of generalizing restrictions to objects besides functions.

In sheaf theory, one assigns an object [math]\displaystyle{ F(U) }[/math] in a category to each open set [math]\displaystyle{ U }[/math] of a topological space, and requires that the objects satisfy certain conditions. The most important condition is that there are restriction morphisms between every pair of objects associated to nested open sets; that is, if [math]\displaystyle{ V\subseteq U, }[/math] then there is a morphism [math]\displaystyle{ \operatorname{res}_{V,U} : F(U) \to F(V) }[/math] satisfying the following properties, which are designed to mimic the restriction of a function:

• For every open set [math]\displaystyle{ U }[/math] of [math]\displaystyle{ X, }[/math] the restriction morphism [math]\displaystyle{ \operatorname{res}_{U,U} : F(U) \to F(U) }[/math] is the identity morphism on [math]\displaystyle{ F(U). }[/math]
• If we have three open sets [math]\displaystyle{ W \subseteq V \subseteq U, }[/math] then the composite [math]\displaystyle{ \operatorname{res}_{W,V} \circ \operatorname{res}_{V,U} = \operatorname{res}_{W,U}. }[/math]
• (Locality) If [math]\displaystyle{ \left(U_i\right) }[/math] is an open covering of an open set [math]\displaystyle{ U, }[/math] and if [math]\displaystyle{ s, t \in F(U) }[/math] are such that [math]\displaystyle{ s\big\vert_{U_i} = t\big\vert_{U_i} }[/math] for each set [math]\displaystyle{ U_i }[/math] of the covering, then [math]\displaystyle{ s = t }[/math]; and
• (Gluing) If [math]\displaystyle{ \left(U_i\right) }[/math] is an open covering of an open set [math]\displaystyle{ U, }[/math] and if for each [math]\displaystyle{ i }[/math] a section [math]\displaystyle{ x_i \in F\left(U_i\right) }[/math] is given such that for each pair [math]\displaystyle{ U_i, U_j }[/math] of the covering sets the restrictions of [math]\displaystyle{ s_i }[/math] and [math]\displaystyle{ s_j }[/math] agree on the overlaps: [math]\displaystyle{ s_i\big\vert_{U_i \cap U_j} = s_j\big\vert_{U_i \cap U_j}, }[/math] then there is a section [math]\displaystyle{ s \in F(U) }[/math] such that [math]\displaystyle{ s\big\vert_{U_i} = s_i }[/math] for each [math]\displaystyle{ i. }[/math]

The collection of all such objects is called a sheaf. If only the first two properties are satisfied, it is a pre-sheaf.

Left- and right-restriction

More generally, the restriction (or domain restriction or left-restriction) [math]\displaystyle{ A \triangleleft R }[/math] of a binary relation [math]\displaystyle{ R }[/math] between [math]\displaystyle{ E }[/math] and [math]\displaystyle{ F }[/math] may be defined as a relation having domain [math]\displaystyle{ A, }[/math] codomain [math]\displaystyle{ F }[/math] and graph [math]\displaystyle{ G(A \triangleleft R) = \{(x, y) \in F(R) : x \in A\}. }[/math] Similarly, one can define a right-restriction or range restriction [math]\displaystyle{ R \triangleright B. }[/math] Indeed, one could define a restriction to [math]\displaystyle{ n }[/math]-ary relations, as well as to subsets understood as relations, such as ones of the Cartesian product [math]\displaystyle{ E \times F }[/math] for binary relations. These cases do not fit into the scheme of sheaves.

Anti-restriction

The domain anti-restriction (or domain subtraction) of a function or binary relation [math]\displaystyle{ R }[/math] (with domain [math]\displaystyle{ E }[/math] and codomain [math]\displaystyle{ F }[/math]) by a set [math]\displaystyle{ A }[/math] may be defined as [math]\displaystyle{ (E \setminus A) \triangleleft R }[/math]; it removes all elements of [math]\displaystyle{ A }[/math] from the domain [math]\displaystyle{ E. }[/math] It is sometimes denoted [math]\displaystyle{ A }[/math] ⩤ [math]\displaystyle{ R. }[/math] Similarly, the range anti-restriction (or range subtraction) of a function or binary relation [math]\displaystyle{ R }[/math] by a set [math]\displaystyle{ B }[/math] is defined as [math]\displaystyle{ R \triangleright (F \setminus B) }[/math]; it removes all elements of [math]\displaystyle{ B }[/math] from the codomain [math]\displaystyle{ F. }[/math] It is sometimes denoted [math]\displaystyle{ R }[/math] ⩥ [math]\displaystyle{ B. }[/math]

See also

• Constraint – Condition of an optimization problem which the solution must satisfy
• Local property
• Function (mathematics) § Restriction and extension
• Binary relation § Restriction
• Relational algebra § Selection (σ)