Physics:Sound pressure
| Sound measurements | |
|---|---|
Characteristic | Symbols |
| Sound pressure | p, SPL,LPA |
| Particle velocity | v, SVL |
| Particle displacement | δ |
| Sound intensity | I, SIL |
| Sound power | P, SWL, LWA |
| Sound energy | W |
| Sound energy density | w |
| Sound exposure | E, SEL |
| Acoustic impedance | Z |
| Audio frequency | AF |
| Transmission loss | TL |
Sound pressure or acoustic pressure is the local pressure deviation from the ambient (average or equilibrium) atmospheric pressure, caused by a sound wave. In air, sound pressure can be measured using a microphone, and in water with a hydrophone. The SI unit of sound pressure is the pascal (Pa).[1]
Mathematical definition
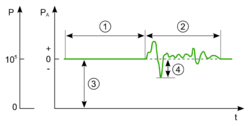
- silence;
- audible sound;
- atmospheric pressure;
- sound pressure
A sound wave in a transmission medium causes a deviation (sound pressure, a dynamic pressure) in the local ambient pressure, a static pressure.
Sound pressure, denoted p, is defined by where
- ptotal is the total pressure,
- pstat is the static pressure.
Sound measurements
Sound intensity
In a sound wave, the complementary variable to sound pressure is the particle velocity. Together, they determine the sound intensity of the wave.
Sound intensity, denoted I and measured in W·m−2 in SI units, is defined by where
- p is the sound pressure,
- v is the particle velocity.
Acoustic impedance
Acoustic impedance, denoted Z and measured in Pa·m−3·s in SI units, is defined by[2] where
- is the Laplace transform of sound pressure[citation needed],
- is the Laplace transform of sound volume flow rate.
Specific acoustic impedance, denoted z and measured in Pa·m−1·s in SI units, is defined by[2] where
- is the Laplace transform of sound pressure,
- is the Laplace transform of particle velocity.
Particle displacement
The particle displacement of a progressive sine wave is given by where
- is the amplitude of the particle displacement,
- is the phase shift of the particle displacement,
- k is the angular wavevector,
- ω is the angular frequency.
It follows that the particle velocity and the sound pressure along the direction of propagation of the sound wave x are given by where
- vm is the amplitude of the particle velocity,
- is the phase shift of the particle velocity,
- pm is the amplitude of the acoustic pressure,
- is the phase shift of the acoustic pressure.
Taking the Laplace transforms of v and p with respect to time yields
Since , the amplitude of the specific acoustic impedance is given by
Consequently, the amplitude of the particle displacement is related to that of the acoustic velocity and the sound pressure by
Inverse-proportional law
When measuring the sound pressure created by a sound source, it is important to measure the distance from the object as well, since the sound pressure of a spherical sound wave decreases as 1/r from the centre of the sphere (and not as 1/r2, like the sound intensity):[3]
This relationship is an inverse-proportional law.
If the sound pressure p1 is measured at a distance r1 from the centre of the sphere, the sound pressure p2 at another position r2 can be calculated:
The inverse-proportional law for sound pressure comes from the inverse-square law for sound intensity: Indeed, where
- is the convolution operator,
- z−1 is the convolution inverse of the specific acoustic impedance,
hence the inverse-proportional law:
The sound pressure may vary in direction from the centre of the sphere as well, so measurements at different angles may be necessary, depending on the situation. An obvious example of a sound source whose spherical sound wave varies in level in different directions is a bullhorn.[citation needed]
Sound pressure level
Sound pressure level (SPL) or acoustic pressure level is a logarithmic measure of the effective pressure of a sound relative to a reference value.
Sound pressure level, denoted Lp and measured in dB,[4] is defined by:[5] where
- p is the root mean square sound pressure,[6]
- p0 is a reference sound pressure,
- 1 Np is the neper,
- 1 B = (1/2 ln 10) Np is the bel,
- 1 dB = (1/20 ln 10) Np is the decibel.
The commonly used reference sound pressure in air is[7]
which is often considered as the threshold of human hearing (roughly the sound of a mosquito flying 3 m away). The proper notations for sound pressure level using this reference are Lp/(20 μPa) or Lp (re 20 μPa), but the suffix notations dB SPL, dB(SPL), dBSPL, or dBSPL are very common, even if they are not accepted by the SI.[8]
Most sound-level measurements will be made relative to this reference, meaning 1 Pa will equal an SPL of 94 dB. In other media, such as underwater, a reference level of 1 μPa is used.[9] These references are defined in ANSI S1.1-2013.[10]
The main instrument for measuring sound levels in the environment is the sound level meter. Most sound level meters provide readings in A, C, and Z-weighted decibels and must meet international standards such as IEC 61672-2013.
Examples
The lower limit of audibility is defined as SPL of 0 dB, but the upper limit is not as clearly defined. While 1 atm (194 dB peak or 191 dB SPL)[11][12] is the largest pressure variation an undistorted sound wave can have in Earth's atmosphere (i. e., if the thermodynamic properties of the air are disregarded; in reality, the sound waves become progressively non-linear starting over 150 dB), larger sound waves can be present in other atmospheres or other media, such as underwater or through the Earth.[13]

Ears detect changes in sound pressure. Human hearing does not have a flat spectral sensitivity (frequency response) relative to frequency versus amplitude. Humans do not perceive low- and high-frequency sounds as well as they perceive sounds between 3,000 and 4,000 Hz, as shown in the equal-loudness contour. Because the frequency response of human hearing changes with amplitude, three weightings have been established for measuring sound pressure: A, B and C.
In order to distinguish the different sound measures, a suffix is used: A-weighted sound pressure level is written either as dBA or LA. B-weighted sound pressure level is written either as dBB or LB, and C-weighted sound pressure level is written either as dBC or LC. Unweighted sound pressure level is called "linear sound pressure level" and is often written as dBL or just L. Some sound measuring instruments use the letter "Z" as an indication of linear SPL.[13]
Distance
The distance of the measuring microphone from a sound source is often omitted when SPL measurements are quoted, making the data useless, due to the inherent effect of the inverse proportional law. In the case of ambient environmental measurements of "background" noise, distance need not be quoted, as no single source is present, but when measuring the noise level of a specific piece of equipment, the distance should always be stated. A distance of one metre (1 m) from the source is a frequently used standard distance. Because of the effects of reflected noise within a closed room, the use of an anechoic chamber allows sound to be comparable to measurements made in a free field environment.[13]
According to the inverse proportional law, when sound level Lp1 is measured at a distance r1, the sound level Lp2 at the distance r2 is
Multiple sources
The formula for the sum of the sound pressure levels of n incoherent radiating sources is
Inserting the formulas in the formula for the sum of the sound pressure levels yields
Examples of sound pressure
| Source of sound | Distance | Sound pressure level[lower-alpha 1] | |
|---|---|---|---|
| (Pa) | (dBSPL) | ||
| Shock wave (distorted sound waves > 1 atm; waveform valleys are clipped at zero pressure)[11][12] | >1.01×105 | >191 | |
| Simple open-ended thermoacoustic device[14] | 1.26×104 | 176 | |
| 165 km | 172 | ||
| .30-06 rifle being fired | 1 m to shooter's side |
7.09×103 | 171 |
| Firecracker[15] | 0.5 m | 7.09×103 | 171 |
| Stun grenade[16] | Ambient | 1.60×103 ...8.00×103 |
158–172 |
| 9-inch (23 cm) party balloon inflated to rupture[17] | At ear | 4.92×103 | 168 |
| 9-inch (23 cm) diameter balloon crushed to rupture[17] | At ear | 1.79×103 | 159 |
| 9-inch (23 cm) party balloon inflated to rupture[17] | 0.5 m | 1.42×103 | 157 |
| 9-inch (23 cm) diameter balloon popped with a pin[17] | At ear | 1.13×103 | 155 |
| LRAD 1000Xi Long Range Acoustic Device[18] | 1 m | 8.93×102 | 153 |
| 9-inch (23 cm) party balloon inflated to rupture[17] | 1 m | 731 | 151 |
| Jet engine[13] | 1 m | 632 | 150 |
| 9-inch (23 cm) diameter balloon crushed to rupture[17] | 0.95 m | 448 | 147 |
| 9-inch (23 cm) diameter balloon popped with a pin[17] | 1 m | 282.5 | 143 |
| Loudest human voice[19] | 1 inch | 110 | 135 |
| Trumpet[20] | 0.5 m | 63.2 | 130 |
| 1 m | 20.0 | 120 | |
| Threshold of pain[21][22][19] | At ear | 20–200 | 120–140 |
| Risk of instantaneous noise-induced hearing loss | At ear | 20.0 | 120 |
| Jet engine | 100–30 m | 6.32–200 | 110–140 |
| Two-stroke chainsaw[23] | 1 m | 6.32 | 110 |
| Jackhammer | 1 m | 2.00 | 100 |
| Traffic on a busy roadway | 10 m | 0.20–0.63 | 80–90 |
| Hearing damage (over long-term exposure, need not be continuous)[24] | At ear | 0.36 | 85 |
| Passenger car | 10 m | 0.02–0.20 | 60–80 |
| EPA-identified maximum to protect against hearing loss and other disruptive effects from noise, such as sleep disturbance, stress, learning detriment, etc.[25] | Ambient | 0.06 | 70 |
| TV (set at home level) | 1 m | 0.02 | 60 |
| Normal conversation | 1 m | 2×10−3–0.02 | 40–60 |
| Very calm room | Ambient | 2.00×10−4 ...6.32×10−4 |
20–30 |
| Light leaf rustling, calm breathing[13] | Ambient | 6.32×10−5 | 10 |
| Auditory threshold at 1 kHz[24] | At ear | 2.00×10−5 | 0 |
| Anechoic chamber, Orfield Labs, A-weighted[26][27] | Ambient | 6.80×10−6 | −9.4 |
| Anechoic chamber, University of Salford, A-weighted[28] | Ambient | 4.80×10−6 | −12.4 |
| Anechoic chamber, Microsoft, A-weighted[29][30] | Ambient | 1.90×10−6 | −20.35 |
- ↑ All values listed are the effective sound pressure unless otherwise stated.
See also
- Acoustics
- Phon (unit)
- Loudness
- Sone (unit)
- Sound level meter
- Stevens's power law
- Weber–Fechner law, especially The case of sound
References
- ↑ "Sound Pressure is the force of sound on a surface area perpendicular to the direction of the sound". http://www.engineeringtoolbox.com/sound-pressure-d_711.html.
- ↑ 2.0 2.1 Wolfe, J.. "What is acoustic impedance and why is it important?". University of New South Wales, Dept. of Physics, Music Acoustics. http://www.phys.unsw.edu.au/jw/z.html.
- ↑ Longhurst, R. S. (1967). Geometrical and Physical Optics. Norwich: Longmans. https://archive.org/details/geometricalphysi0000long.
- ↑ "Letter symbols to be used in electrical technology – Part 3: Logarithmic and related quantities, and their units", IEC 60027-3 Ed. 3.0, International Electrotechnical Commission, 19 July 2002.
- ↑ A pocket-sized introduction to acoustics. Kingston upon Hull: The University of Hull. 2008. doi:10.5281/zenodo.7504060. ISBN 978-90-812588-2-1. https://hal.archives-ouvertes.fr/hal-03188302/document.
- ↑ Bies, David A., and Hansen, Colin. (2003). Engineering Noise Control.
- ↑ Ross Roeser, Michael Valente, Audiology: Diagnosis (Thieme 2007), p. 240.
- ↑ Thompson, A. and Taylor, B. N. Sec. 8.7: "Logarithmic quantities and units: level, neper, bel", Guide for the Use of the International System of Units (SI) 2008 Edition, NIST Special Publication 811, 2nd printing (November 2008), SP811 PDF.
- ↑ Morfey, Christopher L. (2001). Dictionary of Acoustics. San Diego: Academic Press. ISBN 978-0125069403.
- ↑ "Noise Terms Glossary". http://www.memtechacoustical.com/noise-terms-glossary.
- ↑ 11.0 11.1 Self, Douglas (2020-04-17) (in en). Small Signal Audio Design. CRC Press. ISBN 978-1-000-05044-8. https://books.google.com/books?id=L2PdDwAAQBAJ&dq=194+dB+SPL&pg=PP36. "this limit is reached when the rarefaction creates a vacuum, because you can’t have a lower pressure than that. This corresponds to about +194 dB SPL."
- ↑ 12.0 12.1 Guignard, J. C.; King, P. F.; North Atlantic Treaty Organization Advisory Group for Aerospace Research and Development Aerospace Medical Panel (1972) (in en). Aeromedical Aspects of Vibration and Noise. North Atlantic Treaty Organization, Advisory Group for Aerospace Research and Development. https://books.google.com/books?id=LvRJAQAAIAAJ&q=191+dB+SPL. "In air at an assumed atmospheric pressure of 1 bar (100,000 N/m2) this occurs theoretically at approximately 191 dB SPL (working with rms values"
- ↑ 13.0 13.1 13.2 13.3 13.4 Winer, Ethan (2013). "1". The Audio Expert. New York and London: Focal Press. ISBN 978-0-240-82100-9.
- ↑ HATAZAWA, Masayasu; SUGITA, Hiroshi; OGAWA, Takahiro; SEO, Yoshitoki (2004-01-01). "Performance of a Thermoacoustic Sound Wave Generator driven with Waste Heat of Automobile Gasoline Engine". Transactions of the Japan Society of Mechanical Engineers Series B 70 (689): 292–299. doi:10.1299/kikaib.70.292. ISSN 0387-5016. http://ci.nii.ac.jp/naid/130004080803/.
- ↑ Flamme, GregoryA; Liebe, Kevin; Wong, Adam (2009). "Estimates of the auditory risk from outdoor impulse noise I: Firecrackers". Noise and Health 11 (45): 223–230. doi:10.4103/1463-1741.56216. ISSN 1463-1741. PMID 19805932.
- ↑ Brueck S. E., Kardous C. A., Oza A., Murphy W. J (2014). "NIOSH HHE Report No. 2013-0124-3208. Health hazard evaluation report: measurement of exposure to impulsive noise at indoor and outdoor firing ranges during tactical training exercises". U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health. https://www.cdc.gov/niosh/hhe/reports/pdfs/2013-0124-3208.pdf.
- ↑ 17.0 17.1 17.2 17.3 17.4 17.5 17.6 "Did You Know How Loud Balloons Can Be?". http://www.canadianaudiologist.ca/issue/volume-3-issue-6-2016/column/science-matters/.
- ↑ "LRAD Corporation Product Overview for LRAD 1000Xi". http://www.lradx.com/site/content/view/2016/110/.
- ↑ 19.0 19.1 Realistic Maximum Sound Pressure Levels for Dynamic Microphones – Shure.
- ↑ Recording Brass & Reeds.
- ↑ Nave, Carl R. (2006). "Threshold of Pain". HyperPhysics. SciLinks. http://hyperphysics.phy-astr.gsu.edu/Hbase/sound/intens.html.
- ↑ Franks, John R.; Stephenson, Mark R.; Merry, Carol J., eds (June 1996). Preventing Occupational Hearing Loss – A Practical Guide. National Institute for Occupational Safety and Health. pp. 88. https://www.cdc.gov/niosh/docs/96-110/pdfs/96-110.pdf. Retrieved 2009-07-15.
- ↑ "Decibel Table – SPL – Loudness Comparison Chart". sengpielaudio. http://www.sengpielaudio.com/TableOfSoundPressureLevels.htm.
- ↑ 24.0 24.1 William Hamby. "Ultimate Sound Pressure Level Decibel Table". http://www.makeitlouder.com/Decibel%20Level%20Chart.txt.
- ↑ "EPA Identifies Noise Levels Affecting Health and Welfare" (Press release). Environmental Protection Agency. April 2, 1974. Retrieved March 27, 2017.
- ↑ ""THE QUIETEST PLACE ON EARTH" – GUINNESS WORLD RECORDS CERTIFICATE, 2005". Orfield Labs. http://www.orfieldlabs.com/pdfs/chamber.pdf.
- ↑ Middlemiss, Neil (December 18, 2007). "The Quietest Place on Earth – Orfield Labs". http://www.audiojunkies.com/blog/902/the-quietest-place-on-earth-orfield-labs.
- ↑ Eustace, Dave. "Anechoic Chamber". University of Salford. http://www.acoustics.salford.ac.uk/facilities/?content=anechoic.
- ↑ "Microsoft lab sets new record for the world's quietest place". 2015-10-02. http://www.guinnessworldrecords.com/news/2015/10/microsoft-lab-sets-new-record-for-the-worlds-quietest-place-399444. "The computer company has built an anechoic chamber in which highly sensitive tests reported an average background noise reading of an unimaginably quiet −20.35 dBA (decibels A-weighted)."
- ↑ "Check out the world's quietest room". http://news.microsoft.com/stories/building87/audio-lab.php.
- General
- Beranek, Leo L., Acoustics (1993), Acoustical Society of America, ISBN 0-88318-494-X.
- Daniel R. Raichel, The Science and Applications of Acoustics (2006), Springer New York, ISBN 1441920803.
External links
- Sound Pressure and Sound Power, Effect and Cause
- Conversion of Sound Pressure to Sound Pressure Level and Vice Versa
- Table of Sound Levels, Corresponding Sound Pressure and Sound Intensity
- Ohm's Law as Acoustic Equivalent, Calculations
- Relationships of Acoustic Quantities Associated with a Plane Progressive Acoustic Sound Wave
- Sound Pressure and Sound Power, Two Commonly Confused Characteristics of Sound
- How Many Decibels Is Twice as Loud? Sound Level Change and the Respective Factor of Sound Pressure or Sound Intensity
- Decibel (Loudness) Comparison Chart
 |
