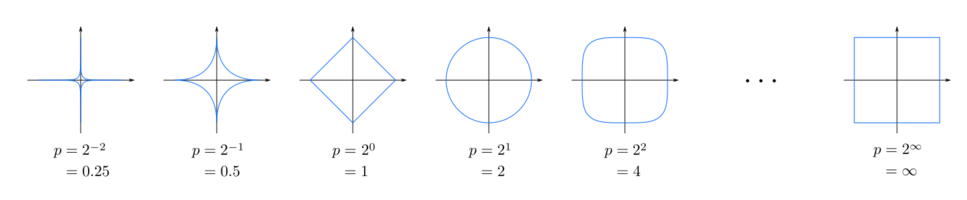Minkowski distance

Short description: Vector distance using pth powers

Not to be confused with the pseudo-Euclidean metric of the Minkowski space.

The Minkowski distance or Minkowski metric is a metric in a normed vector space which can be considered as a generalization of both the Euclidean distance and the Manhattan distance. It is named after the mathematician Hermann Minkowski.

Comparison of Chebyshev, Euclidean and taxicab/Manhattan distances for the hypotenuse of a 3-4-5 triangle on a chessboard (represented by a king, an ant, and a wazir). The wazir moves like a rook but only one square at a time.

Definition

The Minkowski distance of order $p$ (where $p$ is an integer) between two points $$X=(x_1,x_2,\dots ,x_n)\text{ and }Y=(y_1,y_2,\dots ,y_n)\in {\mathbb{ℝ}}^n$$ is defined as: $$D(X,Y)=(\sum _{i=1}^n|x_i-y_i{|}^p{)}^{\frac{1}{p}}.$$

For $p\ge 1,$ the Minkowski distance is a metric as a result of the Minkowski inequality. When $p<1,$ the distance between $(0,0)$ and $(1,1)$ is $2^{1/p}>2,$ but the point $(0,1)$ is at a distance $1$ from both of these points. Since this violates the triangle inequality, for $p<1$ it is not a metric. However, a metric can be obtained for these values by simply removing the exponent of $1/p.$ The resulting metric is also an F-norm.

Minkowski distance is typically used with $p$ being 1 or 2, which correspond to the Manhattan distance and the Euclidean distance, respectively. In the limiting case of $p$ reaching infinity, we obtain the Chebyshev distance: $$\underset{p\to \mathrm{\infty }}{\lim }(\sum _{i=1}^n|x_i-y_i{|}^p{)}^{\frac{1}{p}}={\max }_{i=1}^n|x_i-y_i|.$$

Similarly, for $p$ reaching negative infinity, we have: $$\underset{p\to -\mathrm{\infty }}{\lim }(\sum _{i=1}^n|x_i-y_i{|}^p{)}^{\frac{1}{p}}={\min }_{i=1}^n|x_i-y_i|.$$

The Minkowski distance can also be viewed as a multiple of the power mean of the component-wise differences between $P$ and $Q.$

The following figure shows unit circles (the level set of the distance function where all points are at the unit distance from the center) with various values of $p$:

Applications

The Minkowski metric is very useful in the field of machine learning and AI. Many popular machine learning algorithms use specific distance metrics such as the aforementioned to compare the similarity of two data points. Depending on the nature of the data being analyzed, various metrics can be used. The Minkowski metric is most useful for numerical datasets where one wants to determine the similarity of size between multiple datapoint vectors.

See also

• Generalized mean – N-th root of the arithmetic mean of the given numbers raised to the power n
• $L^p$ space – Function spaces generalizing finite-dimensional p norm spaces
• Norm (mathematics) – Length in a vector space

External links

• Unit Balls for Different p-Norms in 2D and 3D at wolfram.com
• Unit-Norm Vectors under Different p-Norms at wolfram.com
• Simple IEEE 754 implementation in C++
• NPM JavaScript Package/Module