Parallel curve

Parallel curves of the graph of [math]\displaystyle{ y=1.5 \sin(x) }[/math] for distances [math]\displaystyle{ d = 0.25, \dots, 1.5 }[/math]

Two definitions of a parallel curve: 1) envelope of a family of congruent circles, 2) by a fixed normal distance

The parallel curves of a circle (red) are circles, too

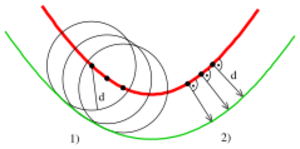
A parallel of a curve is the envelope of a family of congruent circles centered on the curve. It generalises the concept of parallel (straight) lines. It can also be defined as a curve whose points are at a constant normal distance from a given curve. These two definitions are not entirely equivalent as the latter assumes smoothness, whereas the former does not.

In computer-aided design the preferred term for a parallel curve is offset curve. (In other geometric contexts, the term offset can also refer to translation.) Offset curves are important for example in numerically controlled machining, where they describe for example the shape of the cut made by a round cutting tool of a two-axis machine. The shape of the cut is offset from the trajectory of the cutter by a constant distance in the direction normal to the cutter trajectory at every point.

In the area of 2D computer graphics known as vector graphics, the (approximate) computation of parallel curves is involved in one of the fundamental drawing operations, called stroking, which is typically applied to polylines or polybeziers (themselves called paths) in that field.

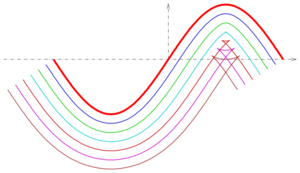
Except in the case of a line or circle, the parallel curves have a more complicated mathematical structure than the progenitor curve. For example, even if the progenitor curve is smooth, its offsets may not be so; this property is illustrated in the top figure, using a sine curve as progenitor curve. In general, even if a curve is rational, its offsets may not be so. For example, the offsets of a parabola are rational curves, but the offsets of an ellipse or of a hyperbola are not rational, even though these progenitor curves themselves are rational.

The notion also generalizes to 3D surfaces, where it is called an offset surface or parallel surface. Increasing a solid volume by a (constant) distance offset is sometimes called dilation. The opposite operation is sometimes called shelling. Offset surfaces are important in numerically controlled machining, where they describe the shape of the cut made by a ball nose end mill of a three-axis machine. Other shapes of cutting bits can be modelled mathematically by general offset surfaces.

Parallel curve of a parametrically given curve

If there is a regular parametric representation [math]\displaystyle{ \vec x= (x(t),y(t)) }[/math] of the given curve available, the second definition of a parallel curve (s. above) leads to the following parametric representation of the parallel curve with distance [math]\displaystyle{ |d| }[/math]:

[math]\displaystyle{ \vec x_d(t)=\vec x(t)+d\vec n(t) }[/math] with the unit normal [math]\displaystyle{ \vec n(t) }[/math].

In cartesian coordinates:

[math]\displaystyle{ x_d(t)= x(t)+\frac{d\; y'(t)}{\sqrt {x'(t)^2+y'(t)^2}} }[/math]

[math]\displaystyle{ y_d(t)= y(t)-\frac{d\; x'(t)}{\sqrt {x'(t)^2+y'(t)^2}} \ . }[/math]

The distance parameter [math]\displaystyle{ d }[/math] may be negative. In this case, one gets a parallel curve on the opposite side of the curve (see diagram on the parallel curves of a circle). One can easily check that a parallel curve of a line is a parallel line in the common sense, and the parallel curve of a circle is a concentric circle.

Geometric properties:

• [math]\displaystyle{ \vec x'_d(t) \parallel \vec x'(t),\quad }[/math] that means: the tangent vectors for a fixed parameter are parallel.
• [math]\displaystyle{ k_d(t)=\frac{k(t)}{1+dk(t)},\quad }[/math] with [math]\displaystyle{ k(t) }[/math] the curvature of the given curve and [math]\displaystyle{ k_d(t) }[/math] the curvature of the parallel curve for parameter [math]\displaystyle{ t }[/math].
• [math]\displaystyle{ R_d(t)=R(t) + d,\quad }[/math] with [math]\displaystyle{ R(t) }[/math] the radius of curvature of the given curve and [math]\displaystyle{ R_d(t) }[/math] the radius of curvature of the parallel curve for parameter [math]\displaystyle{ t }[/math].
• When they exist, the osculating circles to parallel curves at corresponding points are concentric.
• As for parallel lines, a normal line to a curve is also normal to its parallels.
• When parallel curves are constructed they will have cusps when the distance from the curve matches the radius of curvature. These are the points where the curve touches the evolute.
• If the progenitor curve is a boundary of a planar set and its parallel curve is without self-intersections, then the latter is the boundary of the Minkowski sum of the planar set and the disk of the given radius.

If the given curve is polynomial (meaning that [math]\displaystyle{ x(t) }[/math] and [math]\displaystyle{ y(t) }[/math] are polynomials), then the parallel curves are usually not polynomial. In CAD area this is a drawback, because CAD systems use polynomials or rational curves. In order to get at least rational curves, the square root of the representation of the parallel curve has to be solvable. Such curves are called pythagorean hodograph curves and were investigated by R.T. Farouki.

Parallel curves of an implicit curve

Parallel curves of the implicit curve (red) with equation [math]\displaystyle{ x^4+y^4-1=0 }[/math]

Generally the analytic representation of a parallel curve of an implicit curve is not possible. Only for the simple cases of lines and circles the parallel curves can be described easily. For example:

Line [math]\displaystyle{ \; f(x,y)=x+y-1=0\; }[/math] → distance function: [math]\displaystyle{ \; h(x,y)=\frac{x+y-1}{\sqrt{2}}=d\; }[/math] (Hesse normalform)

Circle [math]\displaystyle{ \; f(x,y)=x^2+y^2-1=0\; }[/math] → distance function: [math]\displaystyle{ \; h(x,y)=\sqrt{x^2+y^2}-1=d\; . }[/math]

In general, presuming certain conditions, one can prove the existence of an oriented distance function [math]\displaystyle{ h(x,y) }[/math]. In practice one has to treat it numerically. Considering parallel curves the following is true:

• The parallel curve for distance d is the level set [math]\displaystyle{ h(x,y)=d }[/math] of the corresponding oriented distance function [math]\displaystyle{ h }[/math].

Properties of the distance function:

• [math]\displaystyle{ | \operatorname{grad} h (\vec x)|=1 \; , }[/math]
• [math]\displaystyle{ h(\vec x+d\operatorname{grad} h (\vec x)) = h(\vec x)+d \; , }[/math]
• [math]\displaystyle{ \operatorname{grad}h(\vec x+d\operatorname{grad}h (\vec x))= \operatorname{grad}h (\vec x) \; . }[/math]

Example:
The diagram shows parallel curves of the implicit curve with equation [math]\displaystyle{ \; f(x,y)=x^4+y^4-1=0\; . }[/math]
Remark: The curves [math]\displaystyle{ \; f(x,y)=x^4+y^4-1=d\; }[/math] are not parallel curves, because [math]\displaystyle{ \; | \operatorname{grad} f (x,y)|=1 \; }[/math] is not true in the area of interest.

Further examples

Involutes of a circle

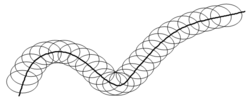
• The involutes of a given curve are a set of parallel curves. For example: the involutes of a circle are parallel spirals (see diagram).

And:

• A parabola has as (two-sided) offsets rational curves of degree 6.
• A hyperbola or an ellipse has as (two-sided) offsets an algebraic curve of degree 8.
• A Bézier curve of degree n has as (two-sided) offsets algebraic curves of degree 4n − 2. In particular, a cubic Bezier curve has as (two-sided) offsets algebraic curves of degree 10.

Parallel curve to a curve with a corner

Parallel curves to a curve with a discontinuous normal around a corner

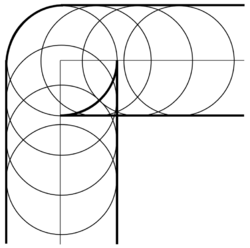
When determining the cutting path of part with a sharp corner for machining, you must define the parallel (offset) curve to a given curve that has a discontinuous normal at the corner. Even though the given curve is not smooth at the sharp corner, its parallel curve may be smooth with a continuous normal, or it may have cusps when the distance from the curve matches the radius of curvature at the sharp corner.

Normal fans

As described above, the parametric representation of a parallel curve, [math]\displaystyle{ \vec x_d(t) }[/math], to a given curver, [math]\displaystyle{ \vec x(t) }[/math], with distance [math]\displaystyle{ |d| }[/math] is:

[math]\displaystyle{ \vec x_d(t) = \vec x(t) + d\vec n(t) }[/math] with the unit normal [math]\displaystyle{ \vec n(t) }[/math].

At a sharp corner ([math]\displaystyle{ t = t_c }[/math]), the normal to [math]\displaystyle{ \vec x(t_c) }[/math] given by [math]\displaystyle{ \vec n(t_c) }[/math] is discontinuous, meaning the one-sided limit of the normal from the left [math]\displaystyle{ \vec n(t_c^-) }[/math] is unequal to the limit from the right [math]\displaystyle{ \vec n(t_c^+) }[/math]. Mathematically,

[math]\displaystyle{ \vec n(t_c^-) = \lim_{t \to t_c^-}\vec n(t) \ne \vec n(t_c^+) = \lim_{t \to t_c^+}\vec n(t) }[/math].

Normal fan for defining parallel curves around a sharp corner

However, we can define a normal fan [math]\displaystyle{ \vec n_f(\alpha) }[/math] that provides an interpolant between [math]\displaystyle{ \vec n(t_c^-) }[/math] and [math]\displaystyle{ \vec n(t_c^+) }[/math], and use [math]\displaystyle{ \vec n_f(\alpha) }[/math] in place of [math]\displaystyle{ \vec n(t_c) }[/math] at the sharp corner:

[math]\displaystyle{ \vec n_f(\alpha) = \frac{(1 - \alpha)\vec n(t_c^-) + \alpha\vec n(t_c^+)}{\lVert (1 - \alpha)\vec n(t_c^-) + \alpha\vec n(t_c^+) \rVert},\quad }[/math]where [math]\displaystyle{ 0 \lt \alpha \lt 1 }[/math].

The resulting definition of the parallel curve [math]\displaystyle{ \vec x_d(t) }[/math] provides the desired behavior:

[math]\displaystyle{ \vec x_d(t) = \begin{cases} \vec x(t) + d\vec n(t), & \text{if }t \lt t_c\text{ or }t \gt t_c \\ \vec x(t_c) + d\vec n_f(\alpha), & \text{if }t = t_c\text{ where }0 \lt \alpha \lt 1 \end{cases} }[/math]

Algorithms

In general, the parallel curve of a Bézier curve is not another Bézier curve, a result proved by Tiller and Hanson in 1984. Thus, in practice, approximation techniques are used. Any desired level of accuracy is possible by repeatedly subdividing the curve, though better techniques require fewer subdivisions to attain the same level of accuracy. A 1997 survey by Elber, Lee and Kim is widely cited, though better techniques have been proposed more recently. A modern technique based on curve fitting, with references and comparisons to other algorithms, as well as open source JavaScript source code, was published in a blog post in September 2022.

Another efficient algorithm for offsetting is the level approach described by Kimmel and Bruckstein (1993).

Parallel (offset) surfaces

Offset surface of a complex irregular shape

Offset surfaces are important in numerically controlled machining, where they describe the shape of the cut made by a ball nose end mill of a three-axis mill. If there is a regular parametric representation [math]\displaystyle{ \vec x(u,v) = (x(u,v),y(u,v),z(u,v)) }[/math] of the given surface available, the second definition of a parallel curve (see above) generalizes to the following parametric representation of the parallel surface with distance [math]\displaystyle{ |d| }[/math]:

[math]\displaystyle{ \vec x_d(u,v)=\vec x(u,v)+d\vec n(u,v) }[/math] with the unit normal [math]\displaystyle{ \vec n_d(u,v) = {{{\partial \vec x \over \partial u} \times {\partial \vec x \over \partial v}} \over {|{{\partial \vec x \over \partial u} \times {\partial \vec x \over \partial v}}|}} }[/math].

Distance parameter [math]\displaystyle{ d }[/math] may be negative, too. In this case one gets a parallel surface on the opposite side of the surface (see similar diagram on the parallel curves of a circle). One easily checks: a parallel surface of a plane is a parallel plane in the common sense and the parallel surface of a sphere is a concentric sphere.

Geometric properties:

• [math]\displaystyle{ {\partial \vec x_d \over \partial u} \parallel {\partial \vec x \over \partial u}, \quad {\partial \vec x_d \over \partial v} \parallel {\partial \vec x \over \partial v}, \quad }[/math] that means: the tangent vectors for fixed parameters are parallel.
• [math]\displaystyle{ \vec n_d(u,v) = \pm\vec n(u,v), \quad }[/math] that means: the normal vectors for fixed parameters match direction.
• [math]\displaystyle{ S_d = (1 + d S)^{-1} S, \quad }[/math] where [math]\displaystyle{ S_d }[/math] and [math]\displaystyle{ S }[/math] are the shape operators for [math]\displaystyle{ \vec x_d }[/math] and [math]\displaystyle{ \vec x }[/math], respectively.

The principal curvatures are the eigenvalues of the shape operator, the principal curvature directions are its eigenvectors, the Gaussian curvature is its determinant, and the mean curvature is half its trace.

• [math]\displaystyle{ S_d^{-1} = S^{-1} + d I, \quad }[/math] where [math]\displaystyle{ S_d^{-1} }[/math] and [math]\displaystyle{ S^{-1} }[/math] are the inverses of the shape operators for [math]\displaystyle{ \vec x_d }[/math] and [math]\displaystyle{ \vec x }[/math], respectively.

The principal radii of curvature are the eigenvalues of the inverse of the shape operator, the principal curvature directions are its eigenvectors, the reciprocal of the Gaussian curvature is its determinant, and the mean radius of curvature is half its trace.

Note the similarity to the geometric properties of parallel curves.

Generalizations

The problem generalizes fairly obviously to higher dimensions e.g. to offset surfaces, and slightly less trivially to pipe surfaces. Note that the terminology for the higher-dimensional versions varies even more widely than in the planar case, e.g. other authors speak of parallel fibers, ribbons, and tubes. For curves embedded in 3D surfaces the offset may be taken along a geodesic.

Another way to generalize it is (even in 2D) to consider a variable distance, e.g. parametrized by another curve. One can for example stroke (envelope) with an ellipse instead of circle as it is possible for example in METAFONT.

An envelope of ellipses forming two general offset curves above and below a given curve

More recently Adobe Illustrator has added somewhat similar facility in version CS5, although the control points for the variable width are visually specified. In contexts where it's important to distinguish between constant and variable distance offsetting the acronyms CDO and VDO are sometimes used.

General offset curves

Assume you have a regular parametric representation of a curve, [math]\displaystyle{ \vec x(t) = (x(t),y(t)) }[/math], and you have a second curve that can be parameterized by its unit normal, [math]\displaystyle{ \vec d(\vec n) }[/math], where the normal of [math]\displaystyle{ \vec d(\vec n) = \vec n }[/math] (this parameterization by normal exists for curves whose curvature is strictly positive or negative, and thus convex, smooth, and not straight). The parametric representation of the general offset curve of [math]\displaystyle{ \vec x(t) }[/math] offset by [math]\displaystyle{ \vec d(\vec n) }[/math] is:

[math]\displaystyle{ \vec x_d(t)=\vec x(t)+ \vec d(\vec n(t)), \quad }[/math] where [math]\displaystyle{ \vec n(t) }[/math] is the unit normal of [math]\displaystyle{ \vec x(t) }[/math].

Note that the trival offset, [math]\displaystyle{ \vec d(\vec n) = d\vec n }[/math], gives you ordinary parallel (aka, offset) curves.

Geometric properties:

• [math]\displaystyle{ \vec x'_d(t) \parallel \vec x'(t),\quad }[/math] that means: the tangent vectors for a fixed parameter are parallel.
• As for parallel lines, a normal to a curve is also normal to its general offsets.
• [math]\displaystyle{ k_d(t)=\dfrac{k(t)}{1+\dfrac{k(t)}{k_n(t)}},\quad }[/math] with [math]\displaystyle{ k_d(t) }[/math] the curvature of the general offset curve, [math]\displaystyle{ k(t) }[/math] the curvature of [math]\displaystyle{ \vec x(t) }[/math], and [math]\displaystyle{ k_n(t) }[/math] the curvature of [math]\displaystyle{ \vec d(\vec n(t)) }[/math] for parameter [math]\displaystyle{ t }[/math].
• [math]\displaystyle{ R_d(t)=R(t) + R_n(t),\quad }[/math] with [math]\displaystyle{ R_d(t) }[/math] the radius of curvature of the general offset curve, [math]\displaystyle{ R(t) }[/math] the radius of curvature of [math]\displaystyle{ \vec x(t) }[/math], and [math]\displaystyle{ R_n(t) }[/math] the radius of curvature of [math]\displaystyle{ \vec d(\vec n(t)) }[/math] for parameter [math]\displaystyle{ t }[/math].
• When general offset curves are constructed they will have cusps when the curvature of the curve matches curvature of the offset. These are the points where the curve touches the evolute.

General offset surfaces

General offset surfaces describe the shape of cuts made by a variety of cutting bits used by three-axis end mills in numerically controlled machining. Assume you have a regular parametric representation of a surface, [math]\displaystyle{ \vec x(u,v) = (x(u,v),y(u,v),z(u,v)) }[/math], and you have a second surface that can be parameterized by its unit normal, [math]\displaystyle{ \vec d(\vec n) }[/math], where the normal of [math]\displaystyle{ \vec d(\vec n) = \vec n }[/math] (this parameterization by normal exists for surfaces whose Gaussian curvature is strictly positive, and thus convex, smooth, and not flat). The parametric representation of the general offset surface of [math]\displaystyle{ \vec x(t) }[/math] offset by [math]\displaystyle{ \vec d(\vec n) }[/math] is:

[math]\displaystyle{ \vec x_d(u,v)=\vec x(u,v)+ \vec d(\vec n(u,v)), \quad }[/math] where [math]\displaystyle{ \vec n(u,v) }[/math] is the unit normal of [math]\displaystyle{ \vec x(u,v) }[/math].

Note that the trival offset, [math]\displaystyle{ \vec d(\vec n) = d\vec n }[/math], gives you ordinary parallel (aka, offset) surfaces.

Geometric properties:

• As for parallel lines, the tangent plane of a surface is parallel to the tangent plane of its general offsets.
• As for parallel lines, a normal to a surface is also normal to its general offsets.
• [math]\displaystyle{ S_d = (1 + SS_n^{-1})^{-1} S, \quad }[/math] where [math]\displaystyle{ S_d, S, }[/math] and [math]\displaystyle{ S_n }[/math] are the shape operators for [math]\displaystyle{ \vec x_d, \vec x, }[/math] and [math]\displaystyle{ \vec d(\vec n) }[/math], respectively.

The principal curvatures are the eigenvalues of the shape operator, the principal curvature directions are its eigenvectors, the Gaussian curvature is its determinant, and the mean curvature is half its trace.

• [math]\displaystyle{ S_d^{-1} = S^{-1} + S_n^{-1}, \quad }[/math] where [math]\displaystyle{ S_d^{-1}, S^{-1} }[/math] and [math]\displaystyle{ S_n^{-1} }[/math] are the inverses of the shape operators for [math]\displaystyle{ \vec x_d, \vec x, }[/math] and [math]\displaystyle{ \vec d(\vec n) }[/math], respectively.

The principal radii of curvature are the eigenvalues of the inverse of the shape operator, the principal curvature directions are its eigenvectors, the reciprocal of the Gaussian curvature is its determinant, and the mean radius of curvature is half its trace.

Note the similarity to the geometric properties of general offset curves.

Derivation of geometric properties for general offsets

The geometric properties listed above for general offset curves and surfaces can be derived for offsets of arbitrary dimension. Assume you have a regular parametric representation of an n-dimensional surface, [math]\displaystyle{ \vec x(\vec u) }[/math], where the dimension of [math]\displaystyle{ \vec u }[/math] is n-1. Also assume you have a second n-dimensional surface that can be parameterized by its unit normal, [math]\displaystyle{ \vec d(\vec n) }[/math], where the normal of [math]\displaystyle{ \vec d(\vec n) = \vec n }[/math] (this parameterization by normal exists for surfaces whose Gaussian curvature is strictly positive, and thus convex, smooth, and not flat). The parametric representation of the general offset surface of [math]\displaystyle{ \vec x(\vec u) }[/math] offset by [math]\displaystyle{ \vec d(\vec n) }[/math] is:

[math]\displaystyle{ \vec x_d(\vec u) = \vec x(\vec u)+ \vec d(\vec n(\vec u)), \quad }[/math] where [math]\displaystyle{ \vec n(\vec u) }[/math] is the unit normal of [math]\displaystyle{ \vec x(\vec u) }[/math]. (The trival offset, [math]\displaystyle{ \vec d(\vec n) = d\vec n }[/math], gives you ordinary parallel surfaces.)

First, notice that the normal of [math]\displaystyle{ \vec x(\vec u) = }[/math] the normal of [math]\displaystyle{ \vec d(\vec n(\vec u)) = \vec n(\vec u), }[/math] by definition. Now, we'll apply the differential w.r.t. [math]\displaystyle{ \vec u }[/math] to [math]\displaystyle{ \vec x_d }[/math], which gives us its tangent vectors spanning its tangent plane.

[math]\displaystyle{ \partial\vec x_d(\vec u) = \partial\vec x(\vec u)+ \partial\vec d(\vec n(\vec u)) }[/math]

Notice, the tangent vectors for [math]\displaystyle{ \vec x_d }[/math] are the sum of tangent vectors for [math]\displaystyle{ \vec x(\vec u) }[/math] and its offset [math]\displaystyle{ \vec d(\vec n) }[/math], which share the same unit normal. Thus, the general offset surface shares the same tangent plane and normal with [math]\displaystyle{ \vec x(\vec u) }[/math] and [math]\displaystyle{ \vec d(\vec n(\vec u)) }[/math]. That aligns with the nature of envelopes.

We now consider the Weingarten equations for the shape operator, which can be written as [math]\displaystyle{ \partial\vec n = -\partial\vec xS }[/math]. If [math]\displaystyle{ S }[/math] is invertable, [math]\displaystyle{ \partial\vec x = -\partial\vec nS^{-1} }[/math]. Recall that the principal curvatures of a surface are the eigenvalues of the shape operator, the principal curvature directions are its eigenvectors, the Gauss curvature is its determinant, and the mean curvature is half its trace. The inverse of the shape operator holds these same values for the radii of curvature.

Substituting into the equation for the differential of [math]\displaystyle{ \vec x_d }[/math], we get:

[math]\displaystyle{ \partial\vec x_d = \partial\vec x - \partial\vec n S_n^{-1},\quad }[/math] where [math]\displaystyle{ S_n }[/math] is the shape operator for [math]\displaystyle{ \vec d(\vec n(\vec u)) }[/math].

Next, we use the Weingarten equations again to replace [math]\displaystyle{ \partial\vec n }[/math]:

[math]\displaystyle{ \partial\vec x_d = \partial\vec x + \partial\vec x S S_n^{-1},\quad }[/math] where [math]\displaystyle{ S }[/math] is the shape operator for [math]\displaystyle{ \vec x(\vec u) }[/math].

Then, we solve for [math]\displaystyle{ \partial\vec x }[/math] and multiple both sides by [math]\displaystyle{ -S }[/math] to get back to the Weingarten equations, this time for [math]\displaystyle{ \partial\vec x_d }[/math]:

[math]\displaystyle{ \partial\vec x_d (I + S S_n^{-1})^{-1} = \partial\vec x, }[/math]

[math]\displaystyle{ -\partial\vec x_d (I + S S_n^{-1})^{-1}S = -\partial\vec xS = \partial\vec n. }[/math]

Thus, [math]\displaystyle{ S_d = (I + S S_n^{-1})^{-1}S }[/math], and inverting both sides gives us, [math]\displaystyle{ S_d^{-1} = S^{-1} + S_n^{-1} }[/math].

See also

• Bump mapping
• Distance function and signed distance function
• Distance field
• Offset printing
• Tubular neighborhood

References

• Josef Hoschek: Offset curves in the plane. In: CAD. 17 (1985), S. 77–81.
• Takashi Maekawa: An overview of offset curves and surfaces. In: CAD. 31 (1999), S. 165–173.

Further reading

• Farouki, R. T.; Neff, C. A. (1990). "Analytic properties of plane offset curves". Computer Aided Geometric Design 7 (1–4): 83–99. doi:10.1016/0167-8396(90)90023-K. 
• Piegl, Les A. (1999). "Computing offsets of NURBS curves and surfaces". Computer-Aided Design 31 (2): 147–156. doi:10.1016/S0010-4485(98)00066-9. 
• Porteous, Ian R. (2001). Geometric Differentiation: For the Intelligence of Curves and Surfaces (2nd ed.). Cambridge University Press. pp. 1–25. ISBN 978-0-521-00264-6. 
• Patrikalakis, Nicholas M.; Maekawa, Takashi (2010). Shape Interrogation for Computer Aided Design and Manufacturing. Springer Science & Business Media. Chapter 11. Offset Curves and Surfaces. ISBN 978-3-642-04074-0.  Free online version.
• Anton, François; Emiris, Ioannis Z.; Mourrain, Bernard; Teillaud, Monique (May 2005). "International Conference on Computational Science and its Applications". Singapore: Springer Verlag. pp. 683–696. 
• Farouki, Rida T. (2008). Pythagorean-Hodograph Curves: Algebra and Geometry Inseparable. Springer Science & Business Media. pp. 141–178. ISBN 978-3-540-73397-3.  Pages listed are the general and introductory material.
• Au, C. K.; Ma, Y.-S. (2013). "Computation of Offset Curves Using a Distance Function: Addressing a Key Challenge in Cutting Tool Path Generation". in Ma, Y.-S.. Semantic Modeling and Interoperability in Product and Process Engineering: A Technology for Engineering Informatics. Springer Science & Business Media. pp. 259–273. ISBN 978-1-4471-5073-2. 

External links

• Parallel curves on MathWorld
• Visual Dictionary of Plane Curves Xah Lee
• http://library.imageworks.com/pdfs/imageworks-library-offset-curve-deformation-from-Skeletal-Anima.pdf application to animation; patented as U.S. Patent 8,400,455
• http://www2.uah.es/fsegundo/Otros/Offset/16-SanSegundoSendraSendra-1532.pdf