Newton's theorem about ovals
In mathematics, Newton's theorem about ovals states that the area cut off by a secant of a smooth convex oval is not an algebraic function of the secant.
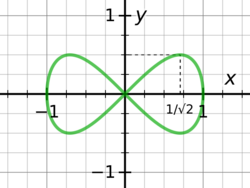
Isaac Newton stated it as lemma 28 of section VI of book 1 of Newton's Principia, and used it to show that the position of a planet moving in an orbit is not an algebraic function of time. There has been some controversy about whether or not this theorem is correct because Newton did not state exactly what he meant by an oval, and for some interpretations of the word oval the theorem is correct, while for others it is false. If "oval" means merely a continuous closed convex curve, then there are counterexamples, such as triangles or one of the lobes of Huygens lemniscate y2 = x2 − x4, while (Arnold 1989) pointed that if "oval" an infinitely differentiable convex curve then Newton's claim is correct and his argument has the essential steps of a rigorous proof.
(Vassiliev 2002) generalized Newton's theorem to higher dimensions.
Statement
An English translation Newton's original statement (Newton 1962) is:
- "There is no oval figure whose area, cut off by right lines at pleasure, can be universally found by means of equations of any number of finite terms and dimensions."
In modern mathematical language, Newton essentially proved the following theorem:
- There is no convex smooth (meaning infinitely differentiable) curve such that the area cut off by a line ax + by = c is an algebraic function of a, b, and c.
In other words, "oval" in Newton's statement should mean "convex smooth curve". The infinite differentiability at all points is necessary: For any positive integer n there are algebraic curves that are smooth at all but one point and differentiable n times at the remaining point for which the area cut off by a secant is algebraic.
Newton observed that a similar argument shows that the arclength of a (smooth convex) oval between two points is not given by an algebraic function of the points.
Newton's proof

Newton took the origin P inside the oval, and considered the spiral of points (r, θ) in polar coordinates whose distance r from P is the area cut off by the lines from P with angles 0 and θ. He then observed that this spiral cannot be algebraic as it has an infinite number of intersections with a line through P, so the area cut off by a secant cannot be an algebraic function of the secant.
This proof requires that the oval and therefore the spiral be smooth; otherwise the spiral might be an infinite union of pieces of different algebraic curves. This is what happens in the various "counterexamples" to Newton's theorem for non-smooth ovals.
References
- Arnold, V. I. (1989), "Topological proof of the transcendence of the abelian integrals in Newton's Principia", Istoriko-Matematicheskie Issledovaniya (31): 7–17, ISSN 0136-0949
- Arnold, V. I.; Vasilev, V. A. (1989), "Newton's Principia read 300 years later", Notices of the American Mathematical Society 36 (9): 1148–1154, ISSN 0002-9920
- Newton, I. (1962), Florian Cajori, ed., Principia Vol. I The Motion of Bodies, Berkeley: University of California Press, ISBN 978-0-520-00928-8 Alternative translation of earlier (2nd) edition of Newton's Principia.
- Pesic, Peter (2001), "The validity of Newton's Lemma 28", Historia Mathematica 28 (3): 215–219, doi:10.1006/hmat.2001.2321, ISSN 0315-0860
- Pourciau, Bruce (2001), "The integrability of ovals: Newton's Lemma 28 and its counterexamples", Archive for History of Exact Sciences 55 (5): 479–499, doi:10.1007/s004070000034, ISSN 0003-9519
- Vassiliev, V. A. (2002), Applied Picard-Lefschetz theory, Mathematical Surveys and Monographs, 97, Providence, R.I.: American Mathematical Society, doi:10.1090/surv/097, ISBN 978-0-8218-2948-6, https://books.google.com/books?isbn=0821829483
 |

