Physics:Atomic coherence
Atomic coherence is the induced coherence between levels of a multi-level atomic system.
The internal state of an atom is characterized by a superposition of excited states and their associated energy levels. In the presence of external electromagnetic fields, the atom's energy levels acquire perturbations to the excited states that describe the atom's internal state. When the acquired phase is the same over the range of internal states, the atom is coherent. Atomic coherence is characterized by the length of time over which the internal state of the atom can be reliably manipulated.[1]
Measuring coherence
The primary way by which atomic coherence is quantified is using the coherence time.
Measurement methods
- Contrast in Ramsey fringes
- The coherence time is the time at which the contrast in Ramsey fringes drops to 1/e. [2]
- Damping of Rabi oscillations
- The coherence time is the time at which the amplitude of the Rabi oscillation has dropped to 1/e. [3]
Examples
Atomic interferometry
An atom interferometer creates coherent atomic beams, where the coherence is with respect to the phase of the atom's de Broglie wave.[4]
Rabi flopping
If an electron in a two level atomic system is excited by narrow line width coherent electro-magnetic radiation, like a laser, that is on resonance with the two level transition, the electron will Rabi flop. During Rabi flopping the electron oscillates between the ground and excited states and can be described by a continuous rotation around the Bloch sphere.
For a perfectly isolated system the Rabi oscillation will continue indefinitely and will undergo no phase change, making it a "coherent state".[5] In physical systems interactions between the system and the environment introduce an unknown phase in the Rabi oscillation between the two levels with respect to the Rabi oscillation in the perfectly isolated system causing "decoherence".
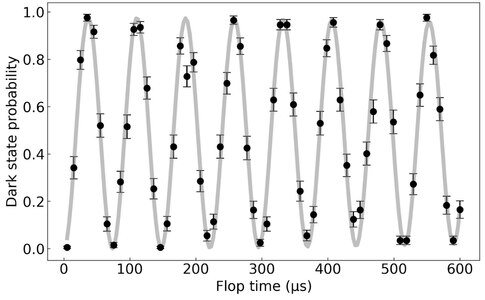
If instead of a single two-level system an ensemble of identical two level systems (such as a chain of identical atoms in an ion trap) is prepared and continuously addressed with a laser, all the atoms may begin to simultaneously Rabi flop.[citation needed] At the beginning all two level systems will have a defined relative phase relation (they will all be in phase) and the system will be coherent.
As atoms begin to undergo random spontaneous emission their Rabi oscillations will accumulate a random relative phase with respect to each other and become decoherent. In actual experiments ambient magnetic field noise and thermal heating from collisions between atoms cause decoherence faster than random spontaneous emission and are the dominant uncertainties when running atomic clocks or trapped ion quantum computers.[6] Atomic coherence can also apply to multi-level systems which require more than a single laser.
Atomic coherence is essential in research on several effects, such as electromagnetically induced transparency (EIT), lasing without inversion (LWI), stimulated raman adiabatic passage (STIRAP) and nonlinear optical interaction with enhanced efficiency.
Atomic systems demonstrating continuous superradiance exhibit long coherence time, a property shared with lasers.[7]
See also
- Physics:Atom interferometer – Interferometer which uses the wave-like nature of atoms
- Physics:Atom optics – Beams of atom matter waves with optical properties
- Physics:Matter wave – Quantum mechanical waves describing matter
- Physics:Rabi cycle – Quantum mechanical phenomenon
References
- ↑ Wineland, D.J.; Monroe, C.; Itano, W.M.; Leibfried, D.; King, B.E.; Meekhof, D.M. (May 1998). "Experimental issues in coherent quantum-state manipulation of trapped atomic ions". Journal of Research of the National Institute of Standards and Technology 103 (3): 259. doi:10.6028/jres.103.019.
- ↑ Wang, Pengfei; Luan, Chun-Yang; Qiao, Mu; Um, Mark; Zhang, Junhua; Wang, Ye; Yuan, Xiao; Gu, Mile et al. (2021-01-11). "Single ion qubit with estimated coherence time exceeding one hour" (in en). Nature Communications 12 (1): 233. doi:10.1038/s41467-020-20330-w. ISSN 2041-1723. PMID 33431845.
- ↑ de Léséleuc, Sylvain; Barredo, Daniel; Lienhard, Vincent; Browaeys, Antoine; Lahaye, Thierry (2018-05-03). "Analysis of imperfections in the coherent optical excitation of single atoms to Rydberg states". Physical Review A 97 (5): 053803. doi:10.1103/PhysRevA.97.053803. Bibcode: 2018PhRvA..97e3803D. https://link.aps.org/doi/10.1103/PhysRevA.97.053803.
- ↑ Cronin, Alexander D.; Schmiedmayer, Jörg; Pritchard, David E. (2009-07-28). "Optics and interferometry with atoms and molecules" (in en). Reviews of Modern Physics 81 (3): 1051–1129. doi:10.1103/RevModPhys.81.1051. ISSN 0034-6861. Bibcode: 2009RvMP...81.1051C. https://link.aps.org/doi/10.1103/RevModPhys.81.1051.
- ↑ Foot, C. J. (2005) (in en). Atomic Physics. Oxford University Press. pp. 127–128. ISBN 978-0-19-850695-9. https://books.google.com/books?id=_CoSDAAAQBAJ.
- ↑ Bruzewics, Colin (2019). "Trapped-ion quantum computing: Progress and challenges". https://pubs.aip.org/aip/apr/article/6/2/021314/570103/Trapped-ion-quantum-computing-Progress-and.
- ↑ Meiser, D.; Holland, M. J. (2010-03-29). "Steady-state superradiance with alkaline-earth-metal atoms". Physical Review A (American Physical Society (APS)) 81 (3): 033847. doi:10.1103/physreva.81.033847. ISSN 1050-2947. Bibcode: 2010PhRvA..81c3847M.
 |  |
