Physics:Electromagnetically induced transparency

From HandWiki
The effect of EIT on a typical absorption line. A weak probe normally experiences absorption shown in blue. A second coupling beam induces EIT and creates a "window" in the absorption region (red). This plot is a computer simulation of EIT in an InAs/GaAs quantum dot

Electromagnetically induced transparency (EIT) is a coherent optical nonlinearity which renders a medium transparent within a narrow spectral range around an absorption line. Extreme dispersion is also created within this transparency "window" which leads to "slow light", described below. It is in essence a quantum interference effect that permits the propagation of light through an otherwise opaque atomic medium.[1]

Observation of EIT involves two optical fields (highly coherent light sources, such as lasers) which are tuned to interact with three quantum states of a material. The "probe" field is tuned near resonance between two of the states and measures the absorption spectrum of the transition. A much stronger "coupling" field is tuned near resonance at a different transition. If the states are selected properly, the presence of the coupling field will create a spectral "window" of transparency which will be detected by the probe. The coupling laser is sometimes referred to as the "control" or "pump", the latter in analogy to incoherent optical nonlinearities such as spectral hole burning or saturation.

EIT is based on the destructive interference of the transition probability amplitude between atomic states. Closely related to EIT are coherent population trapping (CPT) phenomena.

The quantum interference in EIT can be exploited to laser cool atomic particles, even down to the quantum mechanical ground state of motion.[2] This was used in 2015 to directly image individual atoms trapped in an optical lattice.[3]

Medium requirements

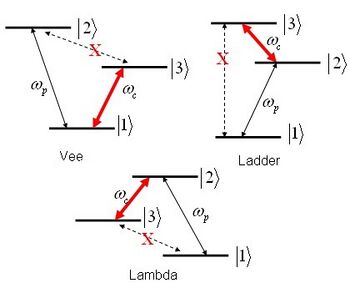
EIT level schemes can be sorted into three categories; vee, ladder, and lambda.

There are specific restrictions on the configuration of the three states. Two of the three possible transitions between the states must be "dipole allowed", i.e. the transitions can be induced by an oscillating electric field. The third transition must be "dipole forbidden." One of the three states is connected to the other two by the two optical fields. The three types of EIT schemes are differentiated by the energy differences between this state and the other two. The schemes are the ladder, vee, and lambda. Any real material system may contain many triplets of states which could theoretically support EIT, but there are several practical limitations on which levels can actually be used.

Also important are the dephasing rates of the individual states. In any real system at non-zero temperature there are processes which cause a scrambling of the phase of the quantum states. In the gas phase, this means usually collisions. In solids, dephasing is due to interaction of the electronic states with the host lattice. The dephasing of state [math]\displaystyle{ |3\rangle }[/math] is especially important; ideally [math]\displaystyle{ |3\rangle }[/math] should be a robust, metastable state.

Currently [when?] EIT research uses atomic systems in dilute gases, solid solutions, or more exotic states such as Bose–Einstein condensate. EIT has been demonstrated in electromechanical[4] and optomechanical[5] systems, where it is known as optomechanically induced transparency. Work is also being done in semiconductor nanostructures such as quantum wells,[6] quantum wires and quantum dots.[7][8]

Theory

EIT was first proposed theoretically by professor Jakob Khanin and graduate student Olga Kocharovskaya at Gorky State University (renamed to Nizhny Novgorod in 1990), Russia;[9] there are now several different approaches to a theoretical treatment of EIT. One approach is to extend the density matrix treatment used to drive Rabi oscillation of a two-state, single field system. In this picture the probability amplitude for the system to transfer between states can interfere destructively, preventing absorption. In this context, "interference" refers to interference between quantum events (transitions) and not optical interference of any kind. As a specific example, consider the lambda scheme shown above. Absorption of the probe is defined by transition from [math]\displaystyle{ |1\rangle }[/math] to [math]\displaystyle{ |2\rangle }[/math]. The fields can drive population from [math]\displaystyle{ |1\rangle }[/math]-[math]\displaystyle{ |2\rangle }[/math] directly or from [math]\displaystyle{ |1\rangle }[/math]-[math]\displaystyle{ |2\rangle }[/math]-[math]\displaystyle{ |3\rangle }[/math]-[math]\displaystyle{ |2\rangle }[/math]. The probability amplitudes for the different paths interfere destructively. If [math]\displaystyle{ |3\rangle }[/math] has a comparatively long lifetime, then the result will be a transparent window completely inside of the [math]\displaystyle{ |1\rangle }[/math]-[math]\displaystyle{ |2\rangle }[/math] absorption line.

Another approach is the "dressed state" picture, wherein the system + coupling field Hamiltonian is diagonalized and the effect on the probe is calculated in the new basis. In this picture EIT resembles a combination of Autler-Townes splitting and Fano interference between the dressed states. Between the doublet peaks, in the center of the transparency window, the quantum probability amplitudes for the probe to cause a transition to either state cancel.

A polariton picture is particularly important in describing stopped light schemes. Here, the photons of the probe are coherently "transformed" into "dark state polaritons" which are excitations of the medium. These excitations exist (or can be "stored") for a length of time dependent only on the dephasing rates.

Slow light and stopped light

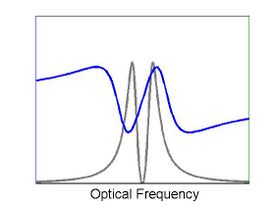
Rapid change of index of refraction (blue) in a region of rapidly changing absorption (gray) associated with EIT. The steep and positive linear region of the refractive index in the center of the transparency window gives rise to slow light

It is important to realize that EIT is only one of many diverse mechanisms which can produce slow light. The Kramers–Kronig relations dictate that a change in absorption (or gain) over a narrow spectral range must be accompanied by a change in refractive index over a similarly narrow region. This rapid and positive change in refractive index produces an extremely low group velocity.[10] The first experimental observation of the low group velocity produced by EIT was by Boller, İmamoğlu, and Harris at Stanford University in 1991 in strontium. In 1999 Lene Hau reported slowing light in a medium of ultracold sodium atoms,[11] achieving this by using quantum interference effects responsible for electromagnetically induced transparency (EIT).[12] Her group performed copious research regarding EIT with Stephen E. Harris. "Using detailed numerical simulations, and analytical theory, we study properties of micro-cavities which incorporate materials that exhibit Electro-magnetically Induced Transparency (EIT) or Ultra Slow Light (USL). We find that such systems, while being miniature in size (order wavelength), and integrable, can have some outstanding properties. In particular, they could have lifetimes orders of magnitude longer than other existing systems, and could exhibit non-linear all-optical switching at single photon power levels. Potential applications include miniature atomic clocks, and all-optical quantum information processing."[13] The current record for slow light in an EIT medium is held by Budker, Kimball, Rochester, and Yashchuk at U.C. Berkeley in 1999. Group velocities as low as 8 m/s were measured in a warm thermal rubidium vapor.[14]

Stopped light, in the context of an EIT medium, refers to the coherent transfer of photons to the quantum system and back again. In principle, this involves switching off the coupling beam in an adiabatic fashion while the probe pulse is still inside of the EIT medium. There is experimental evidence of trapped pulses in EIT medium. Authors created a stationary light pulse inside the atomic coherent media.[15] In 2009 researchers from Harvard University and MIT demonstrated a few-photon optical switch for quantum optics based on the slow light ideas.[16] Lene Hau and a team from Harvard University were the first to demonstrate stopped light.[17]

EIT cooling

Three level lambda structure that is used for EIT cooling, with the Rabi frequencies [math]\displaystyle{ \displaystyle \Omega_g, \Omega_m }[/math]and detunings [math]\displaystyle{ \Delta_g, \Delta_m }[/math] of the cooling and coupling laser, respectively.

EIT has been used to laser cool long strings of atoms to their motional ground state in an ion trap.[18] To illustrate the cooling technique, consider a three level atom as shown with a ground state [math]\displaystyle{ |g\rangle }[/math], an excited state [math]\displaystyle{ |e\rangle }[/math], and a stable or metastable state [math]\displaystyle{ |m\rangle }[/math] that lies in between them. The excited state [math]\displaystyle{ |e\rangle }[/math] is dipole coupled to [math]\displaystyle{ |m\rangle }[/math] and [math]\displaystyle{ |g\rangle }[/math]. An intense "coupling" laser drives the [math]\displaystyle{ |m \rangle \rightarrow |e\rangle }[/math] transition at detuning [math]\displaystyle{ \Delta_m }[/math] above resonance. Due to the quantum interference of transition amplitudes, a weaker "cooling" laser driving the [math]\displaystyle{ |g \rangle \rightarrow |e\rangle }[/math] transition at detuning [math]\displaystyle{ \Delta_g }[/math] above resonance sees a Fano-like feature on the absorption profile. EIT cooling is realized when [math]\displaystyle{ \Delta_g = \Delta_m }[/math], such that the carrier transition [math]\displaystyle{ |g,n \rangle \rightarrow |e, n\rangle }[/math] lies on the dark resonance of the Fano-like feature, where [math]\displaystyle{ n }[/math] is used to label the quantized motional state of the atom. The Rabi frequency [math]\displaystyle{ \Omega_m }[/math] of the coupling laser is chosen such that the [math]\displaystyle{ |g,n \rangle \rightarrow |e, n-1\rangle }[/math] "red" sideband lies on the narrow maximum of the Fano-like feature. Conversely the [math]\displaystyle{ |g,n \rangle \rightarrow |e, n+1\rangle }[/math] "blue" sideband lies in a region of low excitation probability, as shown in the figure below. Due to the large ratio of the excitation probabilities, the cooling limit is lowered in comparison to doppler or sideband cooling (assuming the same cooling rate).[19]

Absorption profile seen by the cooling laser as a function of detuning [math]\displaystyle{ \Delta_g }[/math]. The Rabi frequency [math]\displaystyle{ \Omega_m }[/math]is chosen so that the red sideband (red dashed line) lies on the narrow peak of the Fano-like feature and the blue sideband (blue dashed line) lies in a region of low probability. The carrier (black dashed line) lies on the dark resonance where the detunings are equal, i.e. [math]\displaystyle{ \Delta_g = \Delta_m }[/math], such that absorption is zero.

See also

References

  1. ↑ Liu, Chien; Dutton, Zachary; Behroozi, Cyrus H.; Hau, Lene Vestergaard (2001). "Observation of coherent optical information storage in an atomic medium using halted light pulses". Nature 409 (6819): 490–493. doi:10.1038/35054017. PMID 11206540. Bibcode: 2001Natur.409..490L. http://nrs.harvard.edu/urn-3:HUL.InstRepos:3636968. 
  2. ↑ "Ground State Laser Cooling Using Electromagnetically Induced Transparency". Physical Review Letters 85 (21): 4458–4461. 2000. doi:10.1103/PhysRevLett.85.4458. PMID 11082570. Bibcode: 2000PhRvL..85.4458M. 
  3. ↑ Haller, Elmar; Hudson, James; Kelly, Andrew; Cotta, Dylan A.; Peaudecerf, Bruno; Bruce, Graham D.; Kuhr, Stefan (2015). "Single-atom imaging of fermions in a quantum-gas microscope". Nature Physics 11 (9): 738–742. doi:10.1038/nphys3403. Bibcode: 2015NatPh..11..738H. 
  4. ↑ Teufel, J. D.; Li, Dale; Allman, M. S.; Cicak, K.; Sirois, A. J.; Whittaker, J. D.; Simmonds, R. W. (2011). "Circuit cavity electromechanics in the strong-coupling regime". Nature 471 (7337): 204–208. doi:10.1038/nature09898. PMID 21390127. Bibcode: 2011Natur.471..204T. 
  5. ↑ Safavi-Naeini, A. H.; Alegre, T. P. Mayer; Chan, J.; Eichenfield, M.; Winger, M.; Lin, Q.; Hill, J. T.; Chang, D. E. et al. (2011). "Electromagnetically induced transparency and slow light with optomechanics". Nature 472 (7341): 69–73. doi:10.1038/nature09933. PMID 21412237. Bibcode: 2011Natur.472...69S. 
  6. ↑ Serapiglia, G. B.; Paspalakis, E.; Sirtori, C.; Vodopyanov, K. L.; Phillips, C. C. (2000). "Laser-Induced Quantum Coherence in a Semiconductor Quantum Well". Physical Review Letters 84 (5): 1019–1022. doi:10.1103/PhysRevLett.84.1019. ISSN 0031-9007. PMID 11017430. Bibcode: 2000PhRvL..84.1019S. 
  7. ↑ Xu, Xiaodong; Sun, Bo; Berman, Paul R.; Steel, Duncan G.; Bracker, Allan S.; Gammon, Dan; Sham, L. J. (2008). "Coherent population trapping of an electron spin in a single negatively charged quantum dot". Nature Physics 4 (9): 692–695. doi:10.1038/nphys1054. ISSN 1745-2473. Bibcode: 2008NatPh...4..692X. 
  8. ↑ Brunner, Daniel; Gerardot, Brian D.; Dalgarno, Paul A.; Wüst, Gunter; Karrai, Khaled; Stoltz, Nick G.; Petroff, Pierre M.; Warburton, Richard J. (2009). "A Coherent Single-Hole Spin in a Semiconductor". Science 325 (5936): 70–72. doi:10.1126/science.1173684. ISSN 0036-8075. PMID 19574387. Bibcode: 2009Sci...325...70B. 
  9. ↑ "Texas A&M University physicists have devised a way to stop light | SpaceRef – Your Space Reference". SpaceRef. 2001-01-31. http://www.spaceref.com/news/viewpr.html?pid=3722. 
  10. ↑ Rostovtsev, Yuri; Kocharovskaya, Olga; Welch, George R.; Scully, Marlan O. (2002). "Slow, Ultraslow, Stored, and Frozen Light". Optics and Photonics News 13 (6): 44. doi:10.1364/OPN.13.6.000044. 
  11. ↑ "Lene Hau". Physicscentral.com. http://www.physicscentral.com/explore/people/hau.cfm. 
  12. ↑ Alex Cohen (2006). "Stopping Light". http://uw.physics.wisc.edu/~timbie/P325/Cohen_stopping_light.pdf. 
  13. ↑ Soljacic, Marin; Lidorikis, Elefterios; Joannopoulos, John D.; Hau, Lene V. (2004). "Electromagnetically induced transparency in microcavities". in Taylor, Edward W.. Photonics for Space Environments IX. Proceedings of SPIE. 5554. pp. 174. doi:10.1117/12.562304. 
  14. ↑ Budker, D.; Kimball, D. F.; Rochester, S. M.; Yashchuk, V. V. (1999). "Nonlinear Magneto-optics and Reduced Group Velocity of Light in Atomic Vapor with Slow Ground State Relaxation". Physical Review Letters 83 (9): 1767–1770. doi:10.1103/PhysRevLett.83.1767. Bibcode: 1999PhRvL..83.1767B. 
  15. ↑ Bajcsy, M.; Zibrov, A. S.; Lukin, M. D. (2003). "Stationary pulses of light in an atomic medium". Nature 426 (6967): 638–641. doi:10.1038/nature02176. PMID 14668857. Bibcode: 2003Natur.426..638B. 
  16. ↑ Bajcsy, M.; Hofferberth, S.; Balic, V.; Peyronel, T.; Hafezi, M.; Zibrov, A. S.; Vuletic, V.; Lukin, M. D. (2009). "Efficient All-Optical Switching Using Slow Light within a Hollow Fiber". Physical Review Letters 102 (20): 203902. doi:10.1103/PhysRevLett.102.203902. PMID 19519028. Bibcode: 2009PhRvL.102t3902B. 
  17. ↑ Ginsberg, Naomi S.; Garner, Sean R.; Hau, Lene Vestergaard (2007). "Coherent control of optical information with matter wave dynamics". Nature 445 (7128): 623–626. doi:10.1038/nature05493. PMID 17287804. http://nrs.harvard.edu/urn-3:HUL.InstRepos:3636963. 
  18. ↑ Lechner, Regina; Maier, Christine; Hempell, Cornelius; Jurcevic, Petar; Lanyon, Ben; Monz, Thomas; Brownnutt, Michael; Blatt, Rainer et al. (2016). "Electromagnetically-induced-transparency ground-state cooling of long ion strings". Physical Review A 93 (5): 053401. doi:10.1103/PhysRevA.93.053401. Bibcode: 2016PhRvA..93e3401L. https://journals.aps.org/pra/abstract/10.1103/PhysRevA.93.053401. 
  19. ↑ Morigi, Giovanna; Eschner, Jurgen; Christoph, Keitel (2000). "Ground State Laser Cooling Using Electromagnetically Induced Transparency". Physical Review Letters 85 (21): 4458–4461. doi:10.1103/PhysRevLett.85.4458. PMID 11082570. Bibcode: 2000PhRvL..85.4458M. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.85.4458. 

Primary work

  • O.Kocharovskaya, Ya.I.Khanin, Sov. Phys. JETP, 63, p945 (1986)
  • K.J. Boller, A. İmamoğlu, S. E. Harris, Physical Review Letters 66, p2593 (1991)
  • Eberly, J. H., M. L. Pons, and H. R. Haq, Phys. Rev. Lett. 72, 56 (1994)
  • D. Budker, D. F. Kimball, S. M. Rochester, and V. V. Yashchuk, Physical Review Letters, 83, p1767 (1999)
  • Lene Vestergaard Hau, S.E. Harris, Zachary Dutton, Cyrus H. Behroozi, Nature v.397, p594 (1999)
  • D.F. Phillips, A. Fleischhauer, A. Mair, R.L. Walsworth, M.D. Lukin, Physical Review Letters 86, p783 (2001)
  • Naomi S. Ginsberg, Sean R. Garner, Lene Vestergaard Hau, Nature 445, 623 (2007)

Review



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Electromagnetically_induced_transparency&oldid=3284673"