Physics:Bose–Einstein condensation (network theory)
| Network science | ||||
|---|---|---|---|---|
| Network types | ||||
| Graphs | ||||
|
||||
| Models | ||||
|
||||
| ||||
Bose–Einstein condensation in networks[1] is a phase transition observed in complex networks that can be described by the Bianconi–Barabási model.[2] This phase transition predicts a "winner-takes-all" phenomena in complex networks and can be mathematically mapped to the mathematical model explaining Bose–Einstein condensation in physics.
Background
In physics, a Bose–Einstein condensate is a state of matter that occurs in certain gases at very low temperatures. Any elementary particle, atom, or molecule, can be classified as one of two types: a boson or a fermion. For example, an electron is a fermion, while a photon or a helium atom is a boson. In quantum mechanics, the energy of a (bound) particle is limited to a set of discrete values, called energy levels. An important characteristic of a fermion is that it obeys the Pauli exclusion principle, which states that no two fermions may occupy the same state. Bosons, on the other hand, do not obey the exclusion principle, and any number can exist in the same state. As a result, at very low energies (or temperatures), a great majority of the bosons in a Bose gas can be crowded into the lowest energy state, creating a Bose–Einstein condensate.
Bose and Einstein have established that the statistical properties of a Bose gas are governed by the Bose–Einstein statistics. In Bose–Einstein statistics, any number of identical bosons can be in the same state. In particular, given an energy state ε, the number of non-interacting bosons in thermal equilibrium at temperature T = 1/β is given by the Bose occupation number
- [math]\displaystyle{ n(\varepsilon)=\frac{1}{e^{\beta(\varepsilon-\mu)}-1} }[/math]
where the constant μ is determined by an equation describing the conservation of the number of particles
- [math]\displaystyle{ N=\int d\varepsilon \, g(\varepsilon) \, n(\varepsilon) }[/math]
with g(ε) being the density of states of the system.
This last equation may lack a solution at low enough temperatures when g(ε) → 0 for ε → 0. In this case a critical temperature Tc is found such that for T < Tc the system is in a Bose-Einstein condensed phase and a finite fraction of the bosons are in the ground state.
The density of states g(ε) depends on the dimensionality of the space. In particular [math]\displaystyle{ g(\varepsilon)\sim \varepsilon^{\frac{d-2}{2}} }[/math] therefore g(ε) → 0 for ε → 0 only in dimensions d > 2. Therefore, a Bose-Einstein condensation of an ideal Bose gas can only occur for dimensions d > 2.
The concept
The evolution of many complex systems, including the World Wide Web, business, and citation networks, is encoded in the dynamic web describing the interactions between the system’s constituents. The evolution of these networks is captured by the Bianconi-Barabási model, which includes two main characteristics of growing networks: their constant growth by the addition of new nodes and links and the heterogeneous ability of each node to acquire new links described by the node fitness. Therefore the model is also known as fitness model. Despite their irreversible and nonequilibrium nature, these networks follow the Bose statistics and can be mapped to a Bose gas. In this mapping, each node is mapped to an energy state determined by its fitness and each new link attached to a given node is mapped to a Bose particle occupying the corresponding energy state. This mapping predicts that the Bianconi–Barabási model can undergo a topological phase transition in correspondence to the Bose–Einstein condensation of the Bose gas. This phase transition is therefore called Bose-Einstein condensation in complex networks. Consequently addressing the dynamical properties of these nonequilibrium systems within the framework of equilibrium quantum gases predicts that the “first-mover-advantage,” “fit-get-rich (FGR),” and “winner-takes-all” phenomena observed in a competitive systems are thermodynamically distinct phases of the underlying evolving networks.[1]
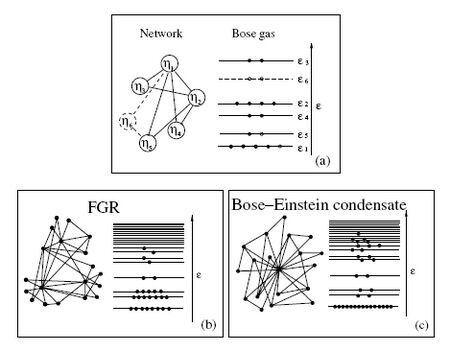
The mathematical mapping of the network evolution to the Bose gas
Starting from the Bianconi-Barabási model, the mapping of a Bose gas to a network can be done by assigning an energy εi to each node, determined by its fitness through the relation[1][3]
- [math]\displaystyle{ \varepsilon_i=-\frac{1}{\beta}\ln{\eta_i} }[/math]
where β = 1 / T . In particular when β = 0 all the nodes have equal fitness, when instead β ≫ 1 nodes with different "energy" have very different fitness. We assume that the network evolves through a modified preferential attachment mechanism. At each time a new node i with energy εi drawn from a probability distribution p(ε) enters in the network and attach a new link to a node j chosen with probability:
- [math]\displaystyle{ \Pi_j=\frac{e^{-\beta\varepsilon_j}k_j}{\sum_r e^{-\beta\varepsilon_r}k_r}. }[/math]
In the mapping to a Bose gas, we assign to every new link linked by preferential attachment to node j a particle in the energy state εj.
The continuum theory predicts that the rate at which links accumulate on node i with "energy" εi is given by
- [math]\displaystyle{ \frac{\partial k_i(\varepsilon_i,t,t_i)}{\partial t}=m\frac{e^{-\beta\varepsilon_i}k_i(\varepsilon_i,t,t_i)}{Z_t} }[/math]
where [math]\displaystyle{ k_i(\varepsilon_i,t, t_i) }[/math] indicating the number of links attached to node i that was added to the network at the time step [math]\displaystyle{ t_i }[/math]. [math]\displaystyle{ Z_t }[/math] is the partition function, defined as:
- [math]\displaystyle{ Z_t=\sum_i e^{-\beta\varepsilon_i}k_i(\varepsilon_i,t,t_i). }[/math]
The solution of this differential equation is:
- [math]\displaystyle{ k_i(\varepsilon_i,t,t_i)=m\left(\frac{t}{t_i}\right)^{f(\varepsilon_i)} }[/math]
where the dynamic exponent [math]\displaystyle{ f(\varepsilon) }[/math] satisfies [math]\displaystyle{ f(\varepsilon)=e^{-\beta(\varepsilon-\mu)} }[/math], μ plays the role of the chemical potential, satisfying the equation
- [math]\displaystyle{ \int d\varepsilon \, p(\varepsilon) \frac{1}{e^{\beta(\varepsilon-\mu)}-1}=1 }[/math]
where p(ε) is the probability that a node has "energy" ε and "fitness" η = e−βε. In the limit, t → ∞, the occupation number, giving the number of links linked to nodes with "energy" ε, follows the familiar Bose statistics
- [math]\displaystyle{ n(\varepsilon)=\frac{1}{e^{\beta(\varepsilon -\mu)}-1}. }[/math]
The definition of the constant μ in the network models is surprisingly similar to the definition of the chemical potential in a Bose gas. In particular for probabilities p(ε) such that p(ε) → 0 for ε → 0 at high enough value of β we have a condensation phase transition in the network model. When this occurs, one node, the one with higher fitness acquires a finite fraction of all the links. The Bose–Einstein condensation in complex networks is, therefore, a topological phase transition after which the network has a star-like dominant structure.
Bose–Einstein phase transition in complex networks

The mapping of a Bose gas predicts the existence of two distinct phases as a function of the energy distribution. In the fit-get-rich phase, describing the case of uniform fitness, the fitter nodes acquire edges at a higher rate than older but less fit nodes. In the end the fittest node will have the most edges, but the richest node is not the absolute winner, since its share of the edges (i.e. the ratio of its edges to the total number of edges in the system) reduces to zero in the limit of large system sizes (Fig.2(b)). The unexpected outcome of this mapping is the possibility of Bose–Einstein condensation for T < TBE, when the fittest node acquires a finite fraction of the edges and maintains this share of edges over time (Fig.2(c)).
A representative fitness distribution ρ(η) that leads to a condensations
- [math]\displaystyle{ \rho(\eta)=(\lambda+1)(1-\eta)^\lambda }[/math]
with λ = 1.
However, the existence of the Bose–Einstein condensation or the fit-get-rich phase does not depend on the temperature or β of the system but depends only on the functional form of the fitness distribution ρ(ν) of the system. In the end, β falls out of all topologically important quantities. In fact, it can be shown that Bose–Einstein condensation exists in the fitness model even without mapping to a Bose gas.[4] A similar gelation can be seen in models with superlinear preferential attachment,[5] however, it is not clear whether this is an accident or a deeper connection lies between this and the fitness model.
Bose–Einstein condensation in evolutionary models and ecological systems
This section possibly contains synthesis of material which does not verifiably mention or relate to the main topic. (June 2020) (Learn how and when to remove this template message) |
In evolutionary models, each species reproduces proportionally to its fitness. In the infinite alleles model, each mutation generates a new species with a random fitness. This model was studied by the statistician J. F. C. Kingman and is known as the "house of cards" models.[6] Depending on the fitness distribution, the model shows a condensation phase transition. Kingman did not realize that this phase transition could be mapped to a Bose–Einstein condensation.
References
- ↑ Jump up to: 1.0 1.1 1.2 1.3 1.4 Bianconi, Ginestra; Barabási, Albert-László (2001). "Bose–Einstein condensation in complex networks". Physical Review Letters 86 (24): 5632–5635. doi:10.1103/physrevlett.86.5632. PMID 11415319. Bibcode: 2001PhRvL..86.5632B.
- ↑ Bianconi, Ginestra; Barabási, Albert-László (2001). "Competition and multiscaling in evolving networks.". Europhysics Letters 54 (4): 436–442. doi:10.1209/epl/i2001-00260-6. Bibcode: 2001EL.....54..436B.
- ↑ Albert, Réka; Barabási, Albert-László (2002-01-30). "Statistical mechanics of complex networks". Reviews of Modern Physics 74 (1): 47–97. doi:10.1103/revmodphys.74.47. ISSN 0034-6861. Bibcode: 2002RvMP...74...47A.
- ↑ Dorogovtsev, S. N.; Mendes, J. F. F. (2001-04-26). "Scaling properties of scale-free evolving networks: Continuous approach". Physical Review E 63 (5): 056125. doi:10.1103/physreve.63.056125. ISSN 1063-651X. PMID 11414979.
- ↑ Krapivsky, P. L.; Redner, S.; Leyvraz, F. (2000-11-20). "Connectivity of Growing Random Networks". Physical Review Letters (American Physical Society (APS)) 85 (21): 4629–4632. doi:10.1103/physrevlett.85.4629. ISSN 0031-9007. PMID 11082613. Bibcode: 2000PhRvL..85.4629K.
- ↑ Kingman, J. F. C. (1978). "A simple model for the balance between selection and mutation". Journal of Applied Probability (Cambridge University Press (CUP)) 15 (1): 1–12. doi:10.2307/3213231. ISSN 0021-9002.



